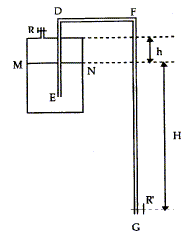
Etude d'un syphon :.

Un vase cylindrique de section S est fermé à sa partie supérieure par un couvercle muni d'un robinet R et laissant passer la branhe ED d'un siphon EDGF. Ce vase renferme de l'eau dont le niveau MN est à une distance h du couvercle et à une hauteur H au dessus du robinet R' situé à l'extrémité du siphon. Le siphon étant rempli d'eau et le robinet R' étant fermé, on ouvre un instant le robinet R et on le referme. La pression au dessus du liquide est alors égale à la pression atmosphérique notée Patm. La section du siphon est négligeable devant celle du vase. On ouvre le robinet R' et on laisse l'eau s'écouler. Données :S= 100 cm² ; h= 0,10 m ; H= 2,0 m ; g= 10 m/s² ; Patm = 1,0 105 Pa ; r= 1030 kg/m3. L'eau peut cesser de s'écouler avant que le récipient soit vide. Expliquer pourquoi à l'aide du théorème de Bernoulli. Equation de Bernoulli relative à une masse de 1 kg du fluide: ½(v2²-v²1) + g(z2-z1)+(P2-P1)/r=0. état 2 ( point G) ; état 1 : surface du liquide dans le vase. v1=0 : la section S est très supérieure à la section du siphon ; v2 =vitesse de l'eau en G l'altitude de G est choisie comme origine z2 =0 ; z1 = H-x avec x, l'abaissement du niveau. P2 = pression atmosphérique ; P1 = p d'où : ½v2² - g(H-x)+(P2-p)/r=0. Si l'eau ne s'écoule plus alors v2=0 ; g(H-x) =(P2-p)/r. H-x= (P2-p)/(gr) ; x = H-(P2-p)/(gr) Dés que l'abaissement du niveau atteint la valeur x = H-(p-P2)/(gr) l'eau ne s'écoule plus. Soit x l'abaissement du niveau MN à un instant donné et p la pression de l'air dans la partie supérieure du vase. On suppose la température constante pendant l'écoulement et on considère l'air comme un gaz parfait. Exprimer la pression p en fonction de x, h et Patm. Expression de la pression p en fonction de x, h et Patm. La température et la quantité de matière de l'air sont constants d'où PV= constante volume initial de l'air au dessus de l'eau du vase : V0= Sh volume de l'air lorsque le niveau descend de x mètres :V= S(h+x) par suite PatmV0= pV ; PatmSh = p S(h+x) ; Patmh = p (h+x) ; p = Patmh /(h+x) ; p = 105*0,1/(0,1+x) = ; p = 104/(0,1+x) (1) Exprimer lorsque l'eau s'arrête de couler ( R' est toujours ouvert) la presion p en fonction de x, H, r et Patm. Pour cela appliquer la relation fondamentale de l'hydrostatique au liquide contenu dans le siphon. Expression de la presion p en fonction de x, H, r et Patm, lorsque l'eau s'arrête de couler ( R' est toujours ouvert) : différence de hauteur entre le point G et la surface du liquide dont le niveau est descendu de x mètres : H-x différence de pression Patm-p = rg(H-x) p = Patm-rg(H-x) ; p = 105 -10300(2-x) ; p =105 - 1,03 104(2-x) (2) en combinant les relations (1) et (2) il vient : 104/(0,1+x) = 105 - 1,03 104(2-x) ; 1/(0,1+x) = 10-1,03(2-x); 10(0,1-x) -1,03(2-x)(0,1-x)= 1 x2 + 7,81 x -0,2 = 0 ; solution x = 0,0255 m ; x= 2,55 cm.   Web www.chimix.com On remplit la cuve d'une hauteur H d'eau avec le bouchon B en place. On installe un tube en U de section s afin de constituer un siphon. Expliquer pourquoi le fonctionnement du siphon est limité à des hauteurs AC inférieures à 10,33 m. Pour cela exprimer de deux manières la pression en A : Le point A est en contact avec l'atmosphère pA ~ 105 Pa ; r = 103 kg m-3 (eau) ; g = 9,8 N /kg. La pression en A est due à la hauteur de la colonne liquide AC : pA=r g AC. d'où AC max = 105 /( r g ) =105 /( 103*9,8 ) =10,2 m. Donner l'expression de la vitesse en E.   Equation de Bernoulli relative à une masse de 1 kg du fluide : ½(v2²-v²1) + g(z2-z1)+(P2-P1)/r=0. état 2 ( point E) ; état 1 : surface du liquide dans le vase. v1~0 : la section S est très supérieure à la section s du siphon ; v2 =vitesse de l'eau en E. Sinon la conservation du débit volumique conduit à Sv1 = sv2 ; v1 = s/S. v2. L'altitude de A est choisie comme origine z1 =0 ; z2 = -(h'-h-x) avec x, l'abaissement du niveau. P2 =P1 = pression atmosphérique. d'où : ½v2² - g(h'-h-x)=0 ; v2 = [2g(h'-h-x)]½. La valeur de x étant inférieure à H. En déduire une condition de fonctionnement du siphon. Si l'eau ne s'écoule plus alors v2=0 ; h'-h-x=0 ; x = h'-h. Or d'après le schéma cette condition ne peut pas être atteinte car H est inférieur à h'-h. Le siphon ne fonctionne plus quand x=H ( réservoir vide).  Quelle est la valeur minimale de h' pour que le siphon fonctionne correctement ? h'-h-x doit être positif : h' > h+x. La valeur maximale de x est H d'où h' > h+H. Donner l'expression du débit maximal du siphon. Débit volumique : D= s v2. Ce débit est maximal lorsque la vitesse v2 est maximale ( x = 0) : v2 max = [2g(h'-h)]½. Dmax = s[2g(h'-h)]½.

retour -menu