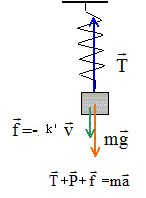Aurélie 30/03/09
 

 

Oscillations libres et forcées : analogies électromécaniques concours Caplp maths sciences 2009.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

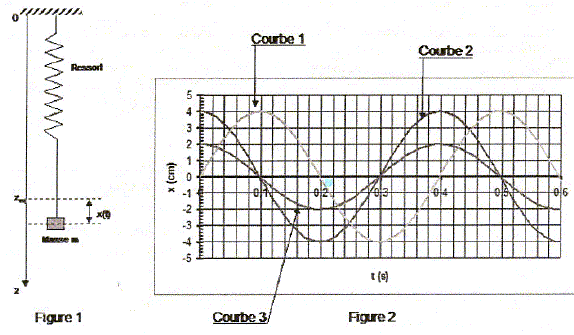
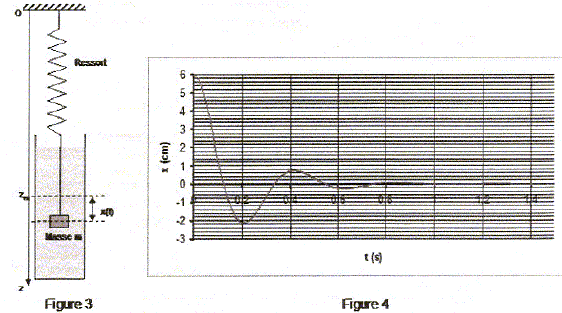
On dispose d'une masse m = 50 g et d'un ressort à spires non jointives. La masse du ressort est négligeable, sa constante de raideur est k = 12,5 N /m et sa longueur à vide l0 = 30 cm. La masse est constituée par un cylindre de laiton de hauteur h = 2 cm et de rayon R = 1 cm. g = 10 m s-2. Le référentiel d'étude est celui du laboratoire et est supposé galiléen.

Oscillations libres sans amortissement.

Le ressort est accroché par son extrémité supérieure O à un point fixe. La masse est suspendue à l'autre extrémité du ressort.

Déterminer léq, longueur du ressort à l'équilibre. En déduire l'abscisse zéq du centre de masse G.

Schéma les forces en présence :

poids : vertical, vers le bas, appliqué au centre d'inertie, valeur : mg

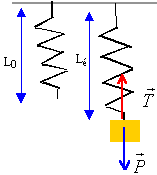
tension du ressort : verticale, dirigée vers la position d'équilibre, appliquée au point de fixation masse ressort, valeur proportionnelle à la déformation du ressort.
A l'équilibre le poids P=mg a même valeur que la tension du ressort : T= k(léq-l0).

d'où léq = zéq= l0 + mg/k = 0,30 + 0,05*10 / 12,5 =0,34 m.

On étudie les oscillations autour de la position d'équilibre précédente. On note x(t) l(écart entre la position de G à l'instant t et sa position d'équilibre.

Déterminer l'équation différentielle qui régit x(t).

Appliquer le principe fondamental de la dynamique ( 2ème loi de Newton) pour établir l'équation du mouvement :
écrire cette loi sur un axe vertical dirigé vers le bas ; l'origine de l'axe est la position d'équilibre stable du système masse ressort :

à l'équilibre : mg = k(Léq-L0)

écarté de sa position d'équilibre le ressort oscille : L= Léq +x

mg-k(L-l0)= m d²x/dt²

mg-k( Léq +x-l0)= m d²x/dt²

mg-k( Léq -l0) - kx =m d²x/dt² ; or mg = k(Léq-L0)

m d²x/dt² + k x=0 (1)
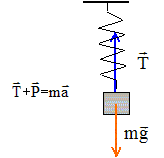
Quelle est la nature du mouvement attendu ? On calculera une grandeur caractéristique de ce mouvvement.

Mouvement sinusoïdal périodique de pulsation w0 = (k/m)½ = (12,5 / 0,05)½ =15,8 rad s-1 ; T0 =6,28 / 15,8 = 0,40 s.
Un dispositif non représenté permet d'enregistrer les variations de l'allongement en fonction du temps. La figure 2 fournit les courbes obtenues pour diverses contitions initiales.

Préciser sans calcul, les conditions initiales ( à t=0) pour les trois cas envisagés.

courbe 1 : x(t=0) = 0, position d'équilibre, lâché avec vitesse initiale.

courbe 2 : x(t=0) = 0,04 m, G est écarté de 4 cm vers le bas, sans vitesse initiale

courbe 3 : x(t=0) = 0,02 m, G est écarté de 2 cm vers le bas, lâché avec vitesse initiale.

Ces courbes sont-elles en accord avec le mouvement attendu ?

Oui, sinusoïdes périodiques correspondant à un oscillateur harmonique non amorti.
Oscillations libres amorties.

Afin d'étudier l'influence d'un frottement fluide, la masse est plongée dans un liquide de masse volumique µ =1130 kg m-3. La masse est constamment immergée.

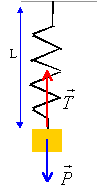
Effectuer un bilan des forces agissant sur la masse à l'équilibre. Déterminer la nouvelle valeur de la position l'éq d'équilibre.
A l'équilibre, la somme vectorielle des trois forces est nulle :

mg + f = k(l'éq-l0) ; l'éq = l0 + mg/k + f/k = léq + f/k.

On montre que l'équation différentielle du mouvement est donnée par :

mx" + k' x' + kx =0

On souhaite obtenir un régime pseudo-périodique. Comment faut-il choisir k' ?

Equation caractéristique associée à l'équation différentielle :

m r2 + k'r +kr=0 ; discriminant D =k'2 - 4mk.

D doit être négatif soit : k'2 < 4mk.
On suppose qu'on écarte la masse de "a" par rapport à la position d'équilibre et qu'on la lâche sans vitesse initiale. La solution x(t) est de la forme :

x(t) = A exp(-lt) [cos ( wt) + b sin (wt)]

Donner l'expression de la pseudo-période T, ainsi que de l, en fonction de l, m, w0=(k/m)½.

On pose l = k'/(2m) ; l'équation différentielle s'écrit : x" + 2l x'+ w02 x=0.

D =4l2-4w02 <0 ; w =(w02-l2 )½ ; T = 2p / w = 2p (w02 -l2)-½.

On enregistre le mouvement de la masse avec le même système . La courbe obtenue est donnée figure 4. On définit le décrément logarithmique comme :

d = 1/n ln[x(t) / (x(t+nT)]

Déterminer d à partir de l'enregistrement et en déduire la valeur de k'.

x(0) = 6 cm ; x(T) = 0,8 cm (lecture graphe) ; n = 1 ; d =ln 6/0,8) =2,0.

x(0) = A ; x(T) = A exp(-lT) ; x(0) / x(T) =exp(+lT) ; d =lT = l 2p (w02 -l2)-½.

4 = l2 4p2 (w02 -l2)-1 ; w02 -l2 = l2p2 ; l = w0 / ( 1+p2 )½ =4,8 rad/s.

Or l = k'/(2m) ; k' = 2m l = 2*0,05*4,8 =0,48 kg rad s-1.

Etablir la relation théorique entre d , k' et T.

d =lT = k'T / (2m).

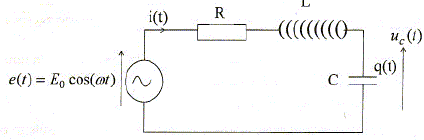
Oscillations forcées par analogie électromécanique.

Pour étudier le régime sinusoïdal forcé du système masse ressort précédent, on peut forcer le mouvement de l'extrémité O à l'aide d'un système bielle manivelle. Le mouvement est alors régit par l'équation : mx" + k'x' + kx = ka cos(wt).

On a m = 0,05 kg ; k = 12,5 N/m ; a = 2 cm et k' = 0,5 S.I. Plutôt que l'étude mécanique, on étudie un analogue électrique formé par un circuit RLC série alimenté par un générateur de tension sinusoïdal e(t) = E0cos(wt).

On considère le schéma électrique ci-dessous :

Déterminer l'équation différentielle suivie par q.

Additivité des tensions : uR + uC + uL =e(t).

uR = R i ; uL =Ldi/dt ; uC = q/C ; i = dq/dt ; di/dt = d2q/dt2.

uR = Rdq/dt = Rq' ; uL =Ld2q/dt2 = Lq" ; uC = q/C.

Lq"+ Rq' + q/C = e(t).

Préciser l'analogie électromécanique à l'aide d'un tableau de correspondance.

mécanique
électrique
mx" +k' x' + kx = ka cos(wt).
Lq"+ Rq' + q/C = E0 cos(wt).
x
q
X0 = ka
E0
m
L
k
1/C
k'
R
vitesse x'
intensité i = dq/dt = q'


On fixe R = 10 ohms.

Quelles valeurs faut-il imposer à L, C et E0 pour que le système électrique ait les mêmes caractéristiques que le système mécanique.

x(t) est numériquement identique à tout instant à q(t).

m = 0,05 kg ; k = 12,5 N/m ; a = 2 cm et k' = 0,5 S.I.

L = 0,05 H ; C = 1/12,5 = 0,08 F ; E0 = ka = 12,5*0,02 =0,25 V.
On s'intéresse à la solution en régime sinusoïdal forcé. On pose w0 = (LC)-½ et Q =1/R (L/C)½ facteur de qualité.

Déterminer l'expression du courant i(t) en notation complexe, circulant dans le circuit RLC.

Additivité des tensions : uR + uC + uL =e(t).

uR = R i ; uL =jLw i ; uC = 1/(jC w) i ;

i = e(t) / [ R + j( Lw- 1/(C w) )].

i = e(t) [ R - j( Lw- 1/(C w) )] / [ R2 + ( Lw- 1/(C w) )2].

En déduire la tension uc(t) aux bornes du condensateur.

q(t) est une primitive de i(t) ce qui revient à diviser i par (jw)

q = e(t) / [ Rjw -( Lw2- 1/(C) )] =C e(t) / [ RCjw - LCw2+ 1]

uc(t) = q(t)/C = e(t) / [ RCjw - LCw2+ 1].

uc(t) =e(t)[ 1- LCw2 -RCjw] / [ (RCw)2 +( 1- LCw2)2].

A partir de l'étude aux hautes et basses fréquences de i(t) et uc(t) donner une interprétation physique du mouvement de la masse m aux hautes et basses fréquences.

Aux hautes fréquences, le condensateur se comporte comme un interrupteur fermé : uc(t) =0 et i (t)=I0.

Aux basses fréquences, le condensateur se comporte comme un interrupteur ouvert : uc(t) =e(t) et i (t)=0.

or kx(t) correspond à uc(t) et la vitesse correspond à i(t).

Aux basses fréquences, la vitesse de la masse tend vers zéro : la masse reste immobile.

Aux hautes fréquences, la vitesse de la masse est égale à v0.

On pose i (t) = I (w) exp (jF(w)). Donner les expressions de I (w) et F(w).

Lq"+ Rq' + q/C = E0 cos(wt) et i est de la forme I cos (wt + j ).

E0 cos(wt) : partie réelle du nombre complexe : E0 exp(jwt)

I cos (wt + j ) :  partie réelle du nombre complexe : I exp(jwt) exp (jj)

i = dq/dt : q est de la forme : I / ( jw)exp(jwt) exp (jj)

q' est de la forme : I exp(jwt) exp (jj)

q" est de la forme : I jw exp(jwt) exp (jj)

Par suite : L I jw exp(jwt) exp (jj) +R I exp(jwt) exp (jj) + I / ( jCw)exp(jwt) exp (jj) = E0 exp(jwt)

L I jw exp (jj) +R I exp (jj) + I / ( jCw) exp (jj) = E0

-L I w2 exp (jj) +R Ijw exp (jj) + I / C exp (jj) = jw E0

[R jw + 1 / C -L w2 ] I exp (jF) = jw E0

I exp (jF) = jw E0/ [ R jw + 1 / C-L w2 ] =jw CE0/ [ RC jw + 1 -LC w2 ]

I exp (jF) =jw CE0[ -RC jw + 1 -LC w2 ]/ [ (RC w)2 + (1 -LC w2)2 ]

I exp (jF) = w CE0[RCw +j( 1 -LC w2) ]/ [ (RC w)2 + (1 -LC w2)2 ]

d'où I = w CE0 / [ (RC w)2 + (1 -LC w2)2 ]½.

I = E0 / [ R2 + (1/(Cw -L w)2 ]½.

tan F = ( 1/(Cw)-L w) / R.


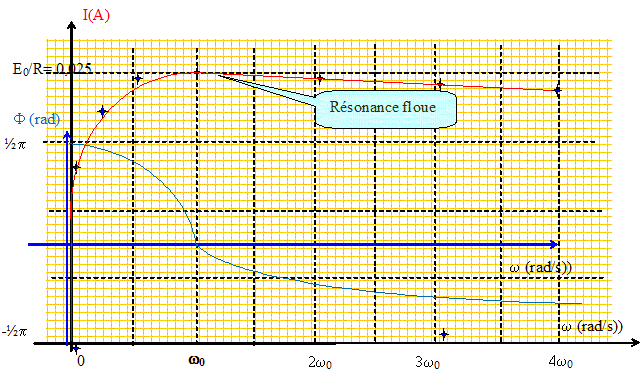
Montrer qu'i y a résonance d'intensité pour une pulsation que l'on déterminera.

dériver I par rappot à w en posant u = [ R2 + (1/(Cw -L w)2 ] ; u' = 2(-1/(Cw2-L)(Cw -L w)

dI/d w = -½ [ R2 + (1/(Cw -L w)2 ]-½ ( -1/(Cw2-L) 2(1/(Cw )-L w)

s'annule pour 1/(Cw )=L w ; w =1/(LC)½ = w0.

L'intensité est nulle pour w =0 et vaut I0 pour w = grand : il s'agit donc d'un maximum.

I = w CE0 / [ (RC w)2 + (1 -LC w2)2 ]½ est maximum ( Imax = E0/R) si : 1 =LC w2 ; w = w0 = (LC)-½.

Donner l'allure des courbes I(w) et F(w).

Q =1/R (L/C)½ = 0,1 (0,05/0,08)½ = 0,08, valeur faible, la résonance est floue.

Définir et calculer la bande passante du circuit.

Ensemble des fréquences ( ou des pulsations) pour lesquelles l'intensité est supérieure ou égale à la l'intensité maximum divisée par racine carrée de 2.

Bande passante : Q=w0 /Dw ; Dw = w0 / Q = 15,8 / 0,08 =


retour -menu