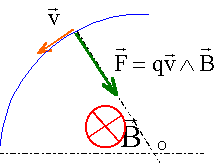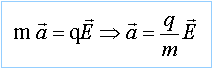|
Inde 04/99 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
||||||
|
|
extrait d'un livre de physique : Les cyclotrons sont les premiers accélérateurs de particules imaginés en 1931 par Lawrence. Leur modéle simplifié est schématisé ci-dessous en vue de dessus : 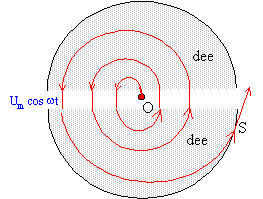 Deux boîtes conductrices cylindriques appelées "dees" baignent dans un champ magnétique uniforme B. Une source d'ions, positifs dans ce cas, est placée dans la région centrale O. L'ensemble est maintenu dans un vide poussé. Entre les "dees" une tension alternative u = Um cos (wt) avec Um = 10 kV, est appliquée aux plaques parrallèles limitant les dees. L'effet de cette tension est d'accélérer les ions pendant une très courte durée lorsqu'ils se trouvent entre les dees. Ils entrent ensuite dans un dees où règne uniquement le champ magnétique qui incurve leur trajectoire selon un demi-cercle. Quand le rayon de courbure de la trajectoire est devenu pratiquement égal au rayon R des dees, les particules atteignent une région où le champ magnétique est localement nul (S). Questions : La force magnétique de Lorentz
|
|||||
|
q : charge électrique en coulomb v : vitesse en m/s B : champ magnétique en tesla F : force de Lorentz en newton. La force magnétique est centripète, perpendiculaire au plan défini par la vitesse et le champ magnétique.
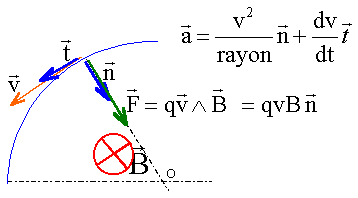
Le poids de la particule est négligeable devant la force magnétique. Ecrire la seconde loi de Newton dans la base de Frenet :
l'accélération est centripète de norme qvB/m = v² /rayon en conséquence : dv/dt =0, le mouvement est uniforme ( norme de la vitesse constante) et qvB = mv² / rayon rayon = mv / (qB) le rayon est constant, le mouvement est circulaire. expression de l'énergie cinétique : Ec = ½ mv² R : rayon au point S ; v = qBR / m Ec = ½ m q²B²R² / m² = q²B²R² / (2m). Ec = [1,6 10-19 *1* 0,8]² / (2*1,37 10-27) = 4,9 10-12 J. entre les dees : la particule est soumise à la force électrique la 2ème loi de Newton s'écrit :
le mouvement est rectiligne uniformément accéléré entre les dees. Pour accélérer de manière efficace les particules : - d'une part la tension alternative doit être maximale : sa demi période est égale à la durée nécessaire pour effectuer ce demi tour. - d'autre par le travail de la force électrique doit être positif : q U >0 impose un changement du signe de la tension à chaque demi tour à la sortie : écrire le théorème de l'énergie cinétique : travail de la force électrique : qUm DEc = qUm = 1,6 10-19 * 104 = 1,6 10-15 J.à chaque ½ tour nombre de tours : énergie finale de la particule divisée par l'énergie acquise à chaque tour 4,9 10-12 / (2* 1,6 10-15 ) = 1531 tours.
|
||||||
|
est
la force subie par la particule .
, le
poids est toujours négligeable.