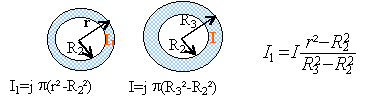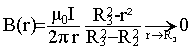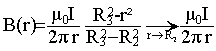Aurélie fevrier 2001

. .
application du théorème d'Ampère

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.

1

théorème d'Ampère

On considère un ensemble de fils parcourus par des courants, la circulation C du champ magnétique le long d'une courbe fermée (G) quelconque est :

quand l'appliquer: 

lorsque la distibution de courants possède d'importantes symétries.

Il faut trouver un contour sur lequel B est uniforme.

reconnaître tous les éléments de symétrie.

calcul direct de la circulation : produit scalaire entre les vecteurs champ et déplacement

calcul par la méthode d'Ampère : attention au sens des courants

égaler les 2 expressions
2

cable coaxial

Un cable coaxial est constitué d'un conducteur cylindrique central de rayon R1 parcouru par un courant d'intensité I. Il est entouré d'un isolant cylindrique de rayon extérieur R2. Le retour - menu du courant se fait par un conducteur cylindrique de rayon intérieur R2 et de rayon extérieur R3.

La densité volumique de courant est uniforme dans les conducteurs ; la longueur est bien supérieure aux rayons.

  1. Déterminer en tout point M de l'espace le champ magnétique.
  2. Etudier la continuité du champ.
  3. Représenter B en fonction de la variable dont il dépend.
corrigé


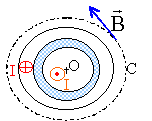
Le champ est orthoradial, il ne dépend que de la distance r, rayon du cercle.

Circulation du champ magnétique le long d'une courbe C, circulaire de centre O, de rayon r :

2pr B(r)

théorème d'Ampère : 2pr B(r) = m0S Ienlacé.

M extérieur : r >R3 : S Ienlacé = 0. donc B(r) =0.

M intérieur au 2 ème conducteur :R2< r <R3 :

expression de l'intensité :

théorème d'Ampère :

2pr B(r) = m0 I-m0 I1.

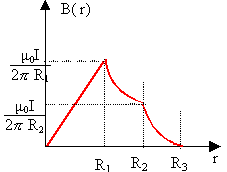
M intérieur à l'isolant :R1< r <R2 :

2pr B(r) = m0 I d'où B(r) =m0 I / (2pr)

B tend vers m0 I / (2pR1) quand r tend vers R1.

M intérieur au 1er conducteur : r <R1 :

expression de l'intensité :

I2 = I r² / R1²

2pr B(r) = m0 I r² / R1² d'où B(r) =m0 I r / (2pR1²)

B tend vers m0 I / (2pR1) quand r tend vers R1.

il y a continuité du champ sur les différentes surfaces de séparation.
3

solénoïde

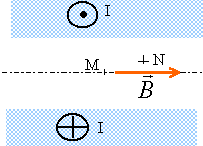
Un solénoïde infiniment long est composé de spires jointives ( n spires par unité de longueur) et il compte plusieurs couches. Le rayon intérieur est noté R1 et le rayon extérieur est noté R2. L'intensité du courant dans une spire est I. Le champ magnétique est nul à l'extérieur.

  1. Donner l'expression du champ magnétique en un point de l'axe du solénoïde.
  2. Montrer que le champ est uniforme à l'intérieur du solénoïde.
  3. Donner l'expression du champ à l'intérieur des enroulements à une distance r de l'axe.
  4. Donner l'expression du flux du champ magnétique à travers une section droite du solénoïde.

 


corrigé
le champ magnétique à l'intérieur du solénoide estparallèle à l'axe de la bobine

Il reste invariant dans une translationparallèle à l'axe z et par rotation autour de cet axe.

on choisit le contour ACDF pour appliquer le théorème d'Ampère.

trajet AC : le champ est nul à l'extérieur du solénoïde

trajet AF et CD : le vecteur champ et trajet sont perpendiculaires: la circulation du champ est nulle

trajet DF : C = B(r) L

intensité des courants enlacés :

n L spires sur la longueur L

n(R2-R1) sur l'épaisseurR2-R1.

n² L(R2-R1) I

théorème d'Ampère :

C = B(r) L = m0 n² L(R2-R1) I

B(r) = m0 n² (R2-R1) I .

Un contour similaire passant par N donne le même résultat : le champ est donc uniforme à l'intérieur du solénoïde.

même méthode lorsque le point M est à l'intérieur de l'enroulement à une distance r de l'axe.

remplacer R1 par r.

B(r) = m0 n² (R2-r) I

flux du champ à travers une section droite du solénoïde :

flux du champ à travers l'intérieur du solénoïde :

F1 = pR1² m0 n² (R2-R1) I

flux du champ à travers les enroulements:

on choisi une couronne de rayon r et d'épaisseur dr : dS=2pr dr

ajouter ces deux flux : F= 1/3 m0 n² I p(R23-R13).
4

nappe de courant

On considére un plan infini parcouru par un courant surfacique de densité js uniforme.

  1. Déterminer en tout point l'expression du champ magnétique.
  2. Etudier la continuité de ce champ.
  3. Mêmes questions, la nappe a une épaisseur 2a et est parcourue par un courant volumique uniforme de densité jv.
corrigé


Le plan contenant M et parallèle au plan yOz est plan de symétrie pour la distribution des courants : donc le champ magnétique est perpendiculaire à ce plan.

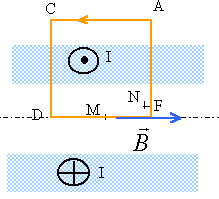
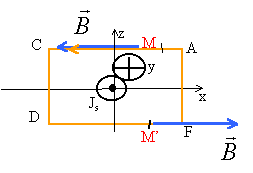
Par translation parallèle à Ox ou à Oy, la distribution des courants est invariante: donc le champ ne dépend que de z.

On choisit le contour d'Ampère ci dessous :(M' symétrique de M)

le plan xOy est un plan de symétrie pour la distribution des courants donc B(-z) = - B(z).

Le long de CD et de AF, la circulation est nul (champ et trajet ortogonaux)

le long de AC: C1= -B(z) L  (signe - car AC sens contraire à Ox)

le long de DF : C2= B(-z) DF = -B(z) L

C= -2 B(z) L

courant enlacé : jsL

théorème d'Ampère :-2 B(z) L = m0jsL

B(z)= -0,5 m0js (sens contraire de l'axe Ox)

alors que B(-z) = 0,5 m0js(sens de l'axe Ox)

discontinuité B(z) - B(-z) = - m0js au passage de la nappe.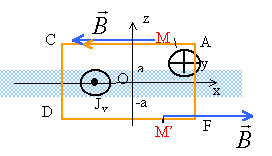

les éléments de symétrie sont identiques à ceux de la question précédente.

La circulation du champ magétique est toujours : C= -2 B(z) L

courants enlacés :

z>a, M extérieur à la nappe de courant : I=2aLjv.

z<a, M intérieur à la nappe de courant : I=2zLjv.

théorème d'Ampère :

z>a : -2 B(z) L = m02aLjv.

B(z) = -m0ajv.

z< -a : B(z) = m0ajv.

-a<z<a : B(z) = -m0zjv.

discontinuité au passage de la nappe : B(z) - B(-z) = -m02ajv.

retour - menu