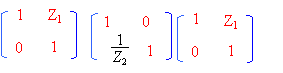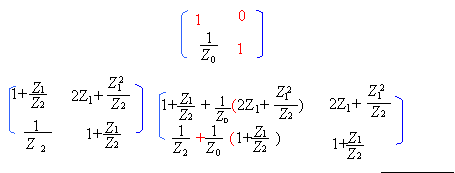|
.
. |
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
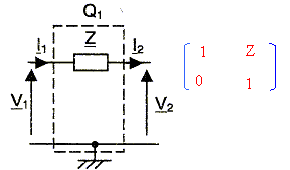
quadripole série |
|
|
|
|
V1 = 1 V2+Z I2. I1 = 0 V2 + 1 I2.
|
|
|
quadripole parallèle |
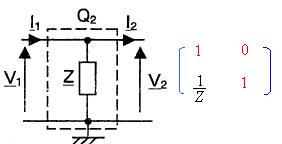
explications |
|
|
|
avec V1 = V2 =Z I d'où I=V1/ Z V1 = 1 V2+0 I2. I1 = 1/Z V1 + 1 I2.
|
|
|
association en cascade |
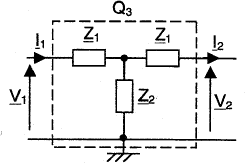
explications |
|
|
|
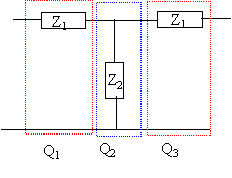
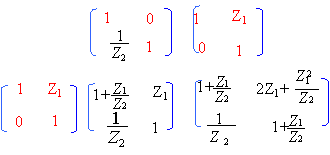
La matrice de transfert [T] de l'ensemble est égale aux produits des matrices associées à chaque quadripole. Le produit des matrices n'est pas commutatif. [T] = [T3] [T2] [T1]
détails du calculs :
|
|
|
association en cascade |
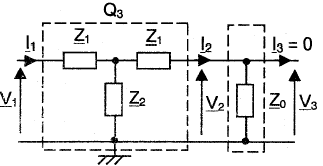
explications |
|
|
|
|