oscillateur mécanique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

1

oscillateur et décollage d'une masse

Un petit objet de masse m est placé sur un plateau horizontal de masse M soutenu par un ressort de raideur k . Ce plateau peut se déplacer verticalement. Soit O l'extrémité inférieure du ressort .On appuie sur le plateau qui se déplace d'une hauteur a et on le lâche sans vitesse initiale. Exprimer la tension T du ressort puis la position d'équilibre Le en fonction de k, m,M,g et L0. Etablir l'équation différentielle du mouvement . En déduire la loi horaire. Exprimer les énergies potentielles de pesanteur et élastique. Traduire la conservation de l'énergie mécanique puis en dérivant retrouver l'équation différentielle précédente. Exprimer la réaction exercée par le plateau sur le petit objet de masse m; puis déterminer la valeur minimale de a, pour laquelle le petit objet décolle. corrigé étude du système objet + plateau tension et déformation sont proportionnelles position d'équilibre A l'équilibre tension et poids sont opposées, ( les normes des forces sont égales) et la longueur du ressort est Le : (m+M)g = k (L0-Le) Le= L0 -(m+M)g/k équation différentielle relation fondamentale de la dynamique projetée sur un axe vertical orienté vers le haut: -(m+M)g- k(L-L0) = (m+M) x" -k (L0-Le) - k(L-L0) = (m+M) x" -k(L- Le ) = (m+M) x" -k x = (m+M) x" avec l'origine de l'axe à la position d'équilibre soit x = L- Le x"+ w0² x=0 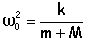solution de l'équation différentielle x = A cos (w0t+ j) A et j sont des constantes déterminées à partir des conditions initiales. à t=0 , x = -a déplacement a vers le bas -a=A cos(j) (1) à t=0 la vitesse est nulle x'= -w0A sin((w0t+ j) 0= -w0A sin( j) d'où j = p en tenant compte de (1) en conséquence A =a x = a cos (w0t+ p) retrouver l'équation différentielle à partir de l'énergie mécanique l'origine de l'énergie potentielle est l'extrémité inférieure du ressort énergie mécanique initiale : (m+M)g (Le-a) à la date t : énergie cinétique 0,5 (m+M)v² ou 0,5 (m+M) x'² énergie potentielle de pesanteur (m+M)g L énergie potentielle élastique 0,5 k (L-L0)² énergie mécanique 0,5 (m+M) x'²+(m+M)g L + 0,5 k (L-L0) ² conservation de l'énergie mécanique 0,5 (m+M) x'²+(m+M)g L + 0,5 k (L-L0) ² = (m+M)g (Le-a) on dérive par rapport au temps (m+M) L' L" + (m+M)g L' + k (L-L0) L'=0 diviser par L' : (m+M) L" + (m+M)g + k(L-L0) = 0 réaction du plateau et décollage 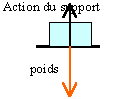Le systéme étudié est l'objet situé sur le plateau. La relation fondamentale de la dynamique s'écrit en projection sur un axe vertical vers le haut: R-mg = mx" avec x" = -w0²a cos(w0t+ p) R = m(g - w0²a cos(w0t+ p)) = m(g + w0²a cos(w0t)) l'objet reste sur le plateau tant que R est positive soit: g + w0²a cos(w0t) >0 Si la condition est vérifiée pour la valeur minimale de cos(w0t) alors l'objet reste sur le plateau g - w0²a >0 a < g /w0² retour - menu