Mathématiques, probabilités, suite, fonction
bac St2S Nlle Calédonie 2017.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.



Exercice 1. 6 points
Un test de dépistage d’une maladie a été élaboré par une entreprise pharmaceutique. Pour étudier sa fiabilité, on soumet à ce test une population comportant des personnes malades et des personnes saines.
On sait que dans la population testée :
— la proportion de personnes malades est de 85%;
— parmi les personnes malades, 95% ont un test positif ;
— parmi les personnes saines, 75% ont un test négatif.
On choisit au hasard une personne dans la population testée; on admet que chaque personne a la même probabilité d’être choisie.
On note :
— M l’évènement : « la personne est malade » ;
— T l’évènement : « le test est positif fg.
Dans cet exercice, la probabilité d’un évènement E est notée p(E) ; la probabilité de l’évènement E sachant
que l’évènement F est réalisé est notée PF (E) ; l’évènement contraire d’un évènement E est noté non E.
1. Interpréter les données de l’énoncé pour déterminer les probabilités p(M) , PM(T ) et Pnon M(non T).
p(M) = 0,85 ; PM(T ) = 0,95 ; Pnon M(non T)=0,75.
2. Traduire la situation par un arbre pondéré de probabilités.

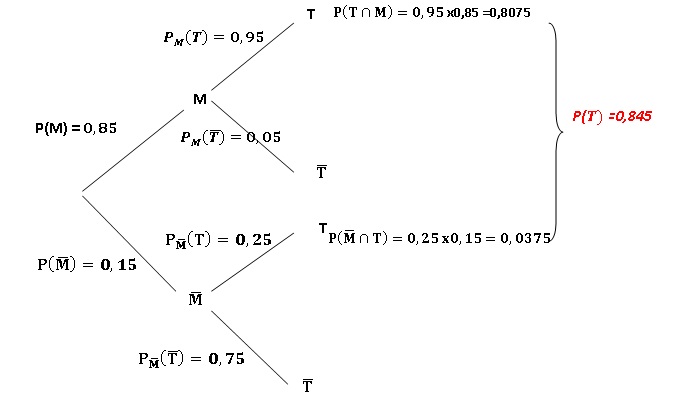3. a. Exprimer par une phrase l’évènement M ∩T .
La personne malade a un test positif.
b. Calculer la probabilité p(M∩T ). En donner la valeur exacte.
4. Montrer que p(T )= 0,845.
5. On considère que le test de dépistage est fiable lorsque la probabilité qu’une personne soit malade sachant que son test est positif est supérieure ou égale à 0,95. Le test est-il fiable?
PT(M) = P(T n M) / P(T) =0,8075 /0,845 =0,9556, valeur supérieure à 0,95 ; le test est fiable.


Exercice 2. 6 points.
Le tableau ci-dessous, extrait d’une feuille de tableur, donne l’évolution de 2010 à 2016 du nombre de naissances dans une commune rurale. La ligne 4 est au format pourcentage.

 A
 B
 C
 D
 E
 F
 G
 H
1
 Année
 2010
 2011
 2012
 2013
 2014
 2015
 2016
2
 Rang de l'année xi
 0
 1
 2
 3
 4
 5
 6
3
 Nombre de naissances yi
 231
 220
 212
 201
 191
 185
 181
4
 Taux d'évolution entre 2 années consécutives %







Il n’est pas demandé de compléter le tableau.
1. Calculer le taux d’évolution du nombre de naissances entre les années 2010 et 2011.
Donner le résultat en pourcentage, arrondi à 0,01%.
(220-231) / 231 x100 = -4,76 %.
2. Quelle formule doit-on saisir dans la cellule C4 pour calculer ce taux d’évolution et pour obtenir les autres taux d’évolution annuels en recopiant la formule vers la droite?
=(C3-B3)/B3
3. Dans un repère orthogonal, représenter le nuage de points de coordonnées (xi ; yi ).
4. a. Déterminer les coordonnées du point moyen G de ce nuage de points.
xG = (1+2+3+4+5+6) / 7=3.
yG=(231+220 +212 +201 +191 +185 +181) / 7 = 203.
b. Placer le point G dans le repère précédent.

5. On suppose que la droite (D) d’équation y = −9x +230 réalise un ajustement affine du nuage de points. On suppose que cet ajustement est valable jusqu’en 2020.
Montrer que le point G appartient à la droite (D) et tracer cette droite. On expliquera la construction de la droite.
-9 xG +230 =-9 x3 +230 = 203 = yG.
La droite passe par le point G et le point de coordonnées (0 ; 230).
6. Déterminer graphiquement une estimation du nombre de naissances en 2017. Laisser apparents les traits de construction et indiquer la valeur ainsi déterminée sur la copie.
7. Déterminer une estimation de l’année au cours de laquelle le nombre de naissances passera sous le seuil des 160 naissances. Expliquer la démarche.
-9x +230 < 160 ; 9x > 230-160 ; 9 x > 70 ; x > 7,78 ; on arrondi à 8.
En 2018 le nombre de naissances sera inférieur à 160.
.


Exercice 3. 8 points.
Un laboratoire pharmaceutique veut fabriquer un antibiotique contre les pneumonies bactériennes.
Dans un premier temps, le laboratoire étudie l’évolution de la masse d’une colonie de bactéries. Dans
un second temps le laboratoire teste l’efficacité de son antibiotique.
Partie A.
Dans cette partie, le laboratoire étudie l’évolution de la masse d’une colonie de bactéries au cours du temps dans un milieu spécifique. On suppose que ce milieu est tel que la masse de la colonie augmente de 20% par heure.
Au début de l’expérience, la masse de la colonie présente dans le milieu est égale à 10 mg.
Dans cette partie, on suppose que l’évolution de la masse de la colonie, exprimée en mg, est modélisée par une suite (un) où n représente le nombre d’heures écoulées depuis le début de l’expérience.
1. Calculer la masse de la colonie de bactéries au bout d’une heure d’expérience.
10 x1,2 = 12 mg.
2. Montrer que la suite (un) est une suite géométrique. On précisera son premier terme u0 et sa raison.
On passe d'un terme au suivant en le multipliant par 1,2. la raison est q = 1,2 et le premier terme est u0 = 10.
3. a. Donner l’expression de un fonction de n.
un = 10 x1,,2n.
b. Calculer la masse de la colonie de bactéries au bout de la 15e heure d’expérience. Donner la valeur arrondie au milligramme.
u15 = 10 x1,215 =154 mg.
4. Au bout de combien de temps la masse de la colonie de bactéries présente dans le milieu dépasserat- elle 500 mg ?
500 =10 x1,2n ; 50 = 1,2n ; ln 50 = n ln1,2 ; n = ln50 / ln1,2 = 21,45.
Au bout de la 22è heure, le nombre de bactéries dépasse 500 mg.
 Partie B.
Le laboratoire teste l’effet de son antibiotique sur une colonie de bactéries pendant une période de 10 heures. Au début du test, la masse de la colonie est de 500 mg.
Dans cette partie, on modélise l’évolution de la masse de la colonie de bactéries par la fonction M définie sur l’intervalle [0; 10] par :
M(x) = x3 −9x2 −48x +500
1. Calculer M(0) et M(10) .
M(0) =500 ; m(10) = 103-9 x100-480+500 =120.
2. On note M′ la fonction dérivée de la fonction M sur l’intervalle [0; 10].
a. Calculer M′(x).
M'(x) = 3x2-18x-48.
b. Vérifier que, pour tout x appartenant à l’intervalle [0; 10], M′(x) = (3x +6)(x −8).
 (3x +6)(x −8) = 3x2-24x+6x-48 = 3x2-18x-48.
3. a. Dresser le tableau de signe de M′(x) sur l’intervalle [0; 10].
b. En déduire le tableau de variation de la fonction M sur l’intervalle [0; 10].

4. Quelle est la valeur du minimum de la fonction M sur l’intervalle [0; 10] ?
f(8) = 83-9 x82 -48x8+500 =52.

5. L’antibiotique est dit efficace s’il parvient, au cours du test, à diviser par cinq la masse initiale de la colonie. L’antibiotique est-il efficace? Justifier la réponse.
500 / 5 = 100.
L'antibiotique parvient à réduire à moins de 100 le nombre de bactéries au bout de 6 heures. Il est efficace.

 .


  

menu