Mathématiques, bac STL biotechnologies Polynésie 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exercice 1. 4 points On injecte un médicament à un patient. Le tableau suivant donne la concentration (enmillimoles par litre) du médicament présent dans son sang à différents instants. Temps ti en heures 1 2 3 4 5 6 7 8 9 10 Concentration Ci (mmol / L) 0,082 0,065 0,058 0,045 0,040 0,030 0,024 0,021 0,019 0,013 yi = ln Ci -2,50 --2,73 -2,85 --3,10 -3,22 -3,51 --3,73 -3,86 -3,96 -4,34 1. Compléter la dernière ligne du tableau. On donnera les valeurs arrondies à 10−2. 2. Tracer, sur du papier millimétré, le nuage de points Mi (ti ; yi ). 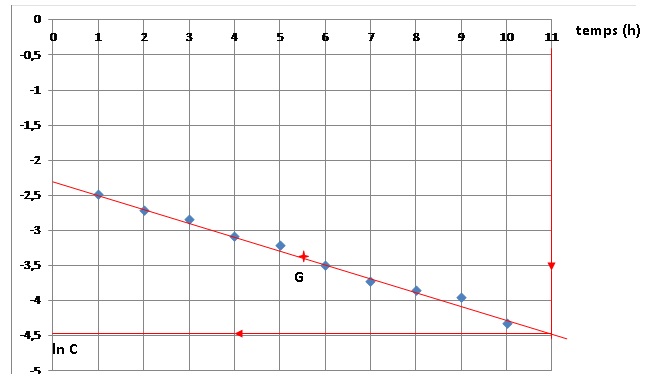3. Déterminer, à l’aide de la calculatrice, une équation de la droite d’ajustement de y en t par la méthode des moindres carrés. y = -0,196 t +2,3. Déterminer une équation de cette droite sous la forme y = at +b. Les valeurs de a et b seront arrondies à 10−3. xmoyen = 5,5 ; ymoyen = -3,38. G(5,5 ; -3,38) La droite passe par le point G : -3,38 =5,5 a+b. La droite passe par le point de coordonnées (0 ; -2,3) : b = -2,3. 5,5 a = -3,38 +2,3= -1,08 ; a = -1,08 / 5,5 =-0,196. y =-0,196t -2,3. Dans la suite, on retient comme droite d’ajustement la droite d’équation : y = −0,2t −2,3. 4. Tracer cette droite sur la feuille de papier millimétré précédente. 5. Déterminer graphiquement la concentration au bout de 11 heures. On arrondira le résultat à 10−3 millimoles par litre. ln C =-4,5 ; C = 0,011 mmol / L. 6. Justifier que la concentration (en millimoles par litre) dumédicament présent dans le sang du patient à l’instant t peut être modélisée par C(t )= 0,1 exp(−0,2t) . C = exp(-0,2t -2,3) = exp(-2,3) x exp (-0,2t) = 0,1 exp(-0,2t). 7. Au bout de combien d’heures la concentration sera-t-elle inférieure ou égale à 10−3 millimoles par litre ? On arrondira le résultat à l’heure. 0,1 exp(-0,2t) <0,001 ; exp(-0,2t) < 0,01 ; -0,2t < ln(0,01) ; -0,2t < -4,6. 0,2 t >4,6 ; t > 4,6 /0,2 ; t > 23 h. .... ... Exercice 2. 4 points. Une entreprise produit 30 tonnes de déchets non recyclables en 2015. Chaque année, l’entreprise veut diminuer la masse de déchets non recyclables de 3% par rapport à l’année précédente. Pour tout entier naturel n >0, on note (pn) la masse de déchets non recyclables à l’année 2015+n. 1. Justifier que (pn) est une suite géométrique dont on précisera le premier terme p0 et la raison. 2. Exprimer pn en fonction de n. On passe d'un terme au suivant en le multipliant par 1-0,03 = 0,97. un+1 = 0,97 un avec un = u0 x0,97n = 30 x0,97n. 3. Quelle est la masse de déchets non recyclables en 2026 ? On donnera la valeur arrondie au kilogramme. n = 11 ; p11 = 30 x 0,9711 =21,459 tonnes. 4. On considère l’algorithme suivant : Variables : u et S réels Initialisation : u prend la valeur 30 S prend la valeur 30 Traitement : Pour i allant de 1 à 5 u prend la valeur 0,97×u S prend la valeur S +u Fin Pour Sortie Afficher S. a. Indiquer les valeurs successives prises par les variables u et S lors du déroulement de l’algorithme, jusqu’àson arrêt. Les valeurs seront arrondies à 10−2. Etape i u S 1 29,10 59,10 2 28,23 87,33 3 28,23 x0,97=27,38 87,33+27,38=114,71 4 30x0,974=26,56 114,71+26,56=141,27 5 30 x0,975=25,76 141,27+25,76=167,03 b. Quelle valeur sera affichée en sortie de cet algorithme ? Que représente-t-elle ? La masse totale des déchets produits entre 2015 et 2020. 5. a. Compléter l’algorithme suivant afin de déterminer en quelle année la somme de tous les déchets non recyclables cumulés depuis l’année 2015 dépassera 300 tonnes. Variables : u et S réels n entier naturel Initialisation : u prend la valeur 30 S prend la valeur 30 n prend la valeur 0 Traitement : Tant que S < 300 u prend la valeur 0,97×u S prend la valeur S +u n prend la valeur n+1 Fin Tant que Sortie Afficher 2015+n. b. Déterminer alors l’année où la somme de tous les déchets non recyclables cumulés depuis l’année 2015 dépassera 300 tonnes. S = p0 ×(1−qn+1) / (1−q) > 300. 30 x(1-0,97n+1) / (1-0,97) > 300. (1-0,97n+1) / 0,03 > 10. (1-0,97n+1) > 10 x0,03 ; 1-0,97n+1 > 0,3 ; 1-0,3 > 0,97n+1 ; 0,7 >0,97n+1 ; ln 0,7 > (n+1) ln 0,97 ; -0,3567 >(n+1) x(-0,03046) ; n+1 > 0,3567 / 0,03046 ; n+1 >11,71 ; n > 11 ( année 2026). EXERCICE 3 5 points On étudie le comportement d’organismes vivants placés dans une enceinte close dont le milieu nutritif est renouvelé en permanence. On modélise cette situation par une fonction J définie sur [0 ; +∞[ qui à chaque instant t (exprimé en heures) associe le nombre d’individus, en milliers, présents dans l’enceinte à cet instant. On admet que pour tout réel t de [0 ; +∞[, f (t ) = 1200−1000e−0,04t . Dans le repère orthogonal donné, on a tracé la courbe représentative (C ) de la fonction f . 1. La courbe (C ) donnée suggère l’existence d’une asymptote horizontale. Donner une équation de cette asymptote et justifier ce résultat par un calcul de limite. Quand t tend vers l'infini, e-0,04t tend vers zéro.En conséquence f(t) tend vers 1200. La droite d'équation y = 1200 est asymptote horizontale. 2. a. En utilisant le graphique, déterminer le nombre d’individus, en milliers, présents dans l’enceinte au bout de 40 heures. On fera apparaître les traits de construction utiles. 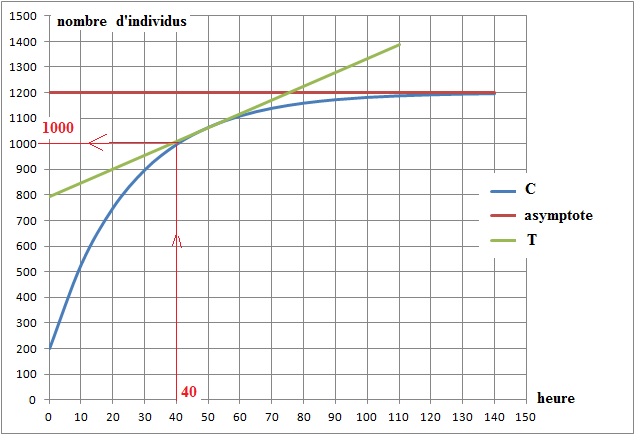b. Déterminer, par le calcul, au bout de combien d’heures le nombre d’individus, en milliers, initialement présents dans l’enceinte aura été multiplié par 5. f(0) = 1200 -1000 = 200. 1000 = 1200 -1000 e-0,04t ; 200=1000 e-0,04t ; ln 0,2 =  ln (1 / 5)= - ln 5= -0,04 t ; t = ln 5 / 0,04 = 25x ln 5 ~40,23 heures. 3. On appelle vitesse d’évolution du nombre d’individus à l’instant t , exprimée en nombre d’individus en milliers par heure, le nombre f ′(t ). a. Pour tout réel t positif ou nul, calculer f ′(t ) où f ′ désigne la fonction dérivée de f . f '(t)=-1000 x(-0,04) e-0,04t=40 e-0,04t. b. Déterminer une valeur arrondie à 10−1 de la vitesse d’évolution du nombre d’individus, en milliers par heure, à l’instant t = 50 heures. f '(50)=40 e-0,04 x50=5,4. c. On appelle (T) la tangente à la courbe (C ) au point d’abscisse 50. Tracer cette tangente sur le graphique donné. On expliquera la méthode employée. Coeficient directeur de T : 5,4 ; équation de T : y = 5,4 t +b. La tangente passe par le point  de coordonnées ( 50 ; f(50) =1065 ) Par suite b = 1065-5,4 x50=795. Equation de la tangente T : y = 5,4 t +795.). T coupe l'axe des ordonnées au point  de coordonnées (0 ; 795). d. La vitesse d’évolution du nombre d’individus, en milliers par heure, diminue au cours du temps. Comment cela se traduit-il sur le graphique ? La pente de la tangente à la courbe C diminue au cours du temps.  Ces tangentes tendent vers l'horizontale y = 1200. EXERCICE 4 7 points Dans cet exercice, les résultats seront arrondis aumillième. Une entreprise fabrique en grand nombre des flacons destinés à contenir un parfum. Un flacon est non conforme s’il ne répond pas au cahier des charges défini par l’entreprise. PARTIE A On note E l’évènement « un flacon prélevé au hasard dans la production d’une journée est non conforme ». La probabilité de cet évènement est égale à 0,07. On prélève au hasard 200 flacons dans la production de cette journée, suffisamment importante pour que l’on puisse assimiler ce prélèvement à un tirage aléatoire avec remise. On considère la variable aléatoire X qui, à tout prélèvement de 200 flacons pris au hasard dans la production, associe le nombre de flacons non conformes dans ce prélèvement.  1. Justifier que la variable aléatoire X suit une loi binomiale dont on précisera les paramètres. Les prélevements sont indépendants.Chaque tirage peut déboucher seulement sur 2 résultats  : la probabilité qu'une pièce soit non conforme est constante p = 0,07. La probabilité qu'une pièce soit conforme est q = 1-p = 0,93. La loi binomiale B(n=200, p = 0,07) est valide. 2. Calculer la probabilité que, dans un tel prélèvement, dix flacons soient non conformes. P(X=10)=0,06516 ~0,0652. 3. Calculer l’espérance de la variable aléatoire X. Interpréter ce résultat. np=200 x0,07 = 14. En moyenne, 14 flacons sont non conformes dans un lot de 200. 4. Calculer l’écart type de la variable aléatoire X. (np(1-p))½ = (200 x0,07 x0,93)½ =3,608. PARTIE B. On décide d’approcher la loi binomiale suivie par X par la loi normale de paramètres μ = 14 et s= 3,61. On considère une variable aléatoire Y suivant cette loi normale. 1. Justifier le choix des valeurs de μ et s. µ = np ; s=(np(1-p))½ de la loi binomiale approchée par la loi normale. 2. En utilisant la loi de Y , déterminer la probabilité qu’un prélèvement de 200 flacons contienne au moins 15 flacons non conformes. P(Y >15) = 1 -P(Y<15) =1-0,609=0,391. 3. On a représenté ci-dessous dans un repère orthogonal, la courbe représentative C de la fonction de densité de la loi normale de paramètres μ = 14 et s = 3,61. 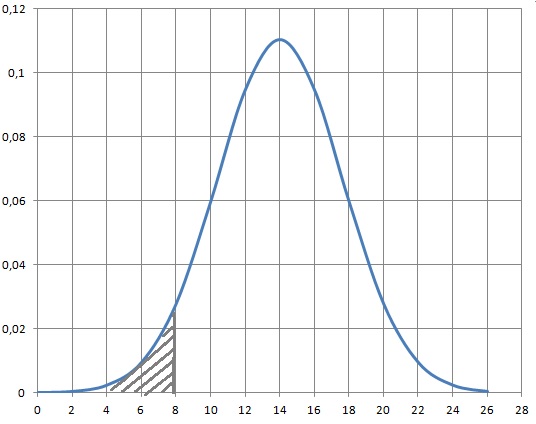L’aire du domaine grisé arrondie à 10−3 vaut 0,048 unité d’aire. Déterminer les probabilités P(Y >20) puis P(8<Y <20). 8 et 20 étant symétriques par rapport à la moyenne 14 : P(Y >20) = P(Y < 8) = 0,048.  P(8<Y <20) = 1-0,048-0,048 =0,904. PARTIE C. L’entreprise affirme à ses clients que 93% des flacons sont conformes. Une enseigne de parfumerie décide d’acheter une grande quantité de flacons. 1. Cette enseigne souhaite vérifier l’affirmation de l’entreprise sur la qualité des flacons. Pour cela, elle prélève un échantillon de 400 flacons au hasard dans une livraison. a. Déterminer un intervalle de fluctuation asymptotique à 95% de la fréquence des flacons conformes dans un échantillon de 400 flacons. n = 400, supérieur à 30 ; np = 400 x 0,07 = 28, supérieur à 5 ; n(1-p) = 400 x0,93=372, supérieur à 5. Les conditions sont requises pour déterminer un intervalle de fluctuation asymptotique à 95 %. 1,96 x(px(1-p) / n )½ = 1,96 x(0,07 x0,93 / 400)½=1,96 x0,01276 ~0,025. Intervalle de fluctuation [0,07-0,025 ; 0,07 +0,025] soit [0,045 ; 0,095]. b. L’enseigne de parfumerie constate que 36 flacons de l’échantillon ne sont pas conformes. Ce résultat remet-il en question la confiance de cette enseigne de parfumerie envers son entreprise ? 36 / 400 = 0,09, cette valeur appartient à l'intervalle de fluctuation ; l'affirmation de l'entreprise n'est pas remise en cause. 2. On cherche à déterminer la taille N des échantillons à partir de laquelle l’intervalle de fluctuation asymptotique a une longueur inférieure ou égale à 0,02. a. Écrire, en fonction de n, un intervalle de fluctuation asymptotique à 95% de la fréquence de flacons conformes dans un échantillon de n flacons puis vérifier que la longueur de cet intervalle est 2×1,96x(0,93 x0,07 /n)½. 2 x1,96 x(px(1-p) / n )½ =2×1,96x(0,93 x0,07 /n)½. b. Avec un logiciel de calcul formel, on a obtenu les informations suivantes : 1 2∗1,96∗sqrt((0,93∗0,07)/x) < 0,02 2 Résoudre x >1563051 / 625 3 1563051 / 625 ~2500,88 Utiliser les résultats obtenus pour en déduire la valeur N cherchée. N = 2501.

menu