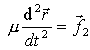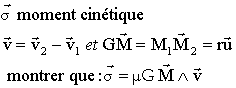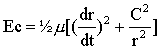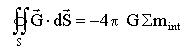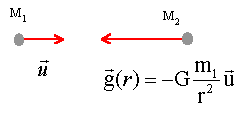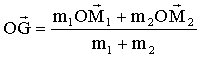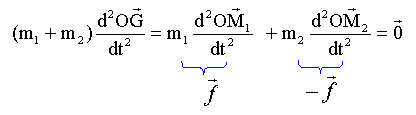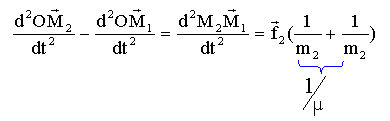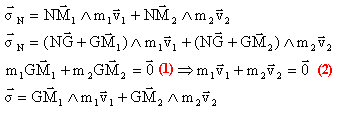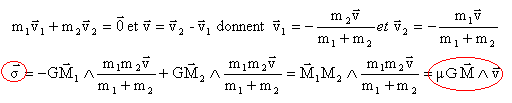Aurélie oct 2001
champ et interactions.

Capes 96 exercice suivant : diffusion de Rutherford

forces centrales

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

forces centrales 
  1. On considère deux objets ponctuels de masse m1 et m2 situés à une distance r l'un de l'autre, aux points M1 et M2.
    - Exprimer la force d'interaction exercée par m1 sur m2. Le vecteur unitaire sera dirigé de M1 vers M2.
    - Montrer que si m1 est une masse à symétrie sphérique de centre M1, la relation précédente est vérifiée à l'extérieur de la sphère (On pourra utiliser le théorème de Gauss).
    - Etablir l'expression de l'énergie potentielle Ep du système constitué par les masses m1 et m2 . On choisira par convention que l'énergie potentielle s'annule lorsque les masses sont infiniment distantes.
  2. On considère le système isolé constitué des deux objets ponctuels de masses m1 et m2 situés en M1 et M2 dans un référentiel galiléen. L'origine du repère est notée O. On note G le centre d'inertie du système.
    - Exprimer le vecteur OG en fonction des vecteurs OM1 et OM2.
    - Préciser en justifiant le mouvement du point G. En déduire que le référentiel barycentrique est galiléen.
    - On appelle f2 la force qu'exerce m1 sur la masse m2 et M1M2 = r . Etablir la relation, dans le référentiel barycentrique,

    dans laquelle on établira l'expression de la masse réduite m en fonction de m1 et m2.

  3. Dans la suite, on se place dans le référentiel barycentrique. L'objet de masse m1 se déplace à la vitesse v1 et l'objet de masse m2 à la vitesse v2.
    - Etablir l'expression du moment cinétique de l'ensemnle du système par rapport à un point N quelconque.
    - Montrer que sa valeur est indépendante de la position du point N.
    -
    - Justifier que le moment cinétique est conservé et que le mouvement est plan.
    - Dans le plan de la trajectoire, orientée par le moment cinétique, on note (r,q), les coordonnées polaires du vecteur GM. Montrer que C=r² q' est constant au cours du temps. Justifier le nom de constante des aires donnée à ½C.

    - Donner l'expression de l'énergie cinétique Ec du système constitué par les deux objets
    - Montrer que cette expression est identique à celle obtenue pour un objet de masse m se déplaçant à la vitesse v.
    - Exprimer Ec en utilisant les coordonnées polaires. En déduire que :

    - Ecrire l'expression de l'énergie mécanique du système.

  4. On considère le système constitué d'un noyau atomique de masse M de charge Ze, et d'une particule a(noyau d'hélium de masse m et de charge 2e. L'interaction gravitationnelle peut être négligée devant l'interaction électrostatique; le justifier en considérant M=3,27 10-25 kg; Z=79 ; m= 6,65 10-27 kg. permittivité du vide e0 = 8,85 10-12 F/m.
    - Par analogie avec les résultats précédents donner l'expression de l'énergie mécanique du système.
Force de gravitation exercée par m1 sur m2 distants de r :

G est la constante de gravitation.

La symétrie sphérique indique que le champ est radial et ne dépend que de r.

théorème de gauss : le flux du champ de gravitation à travers une surface fermée est égal à la somme des masses intérieures multipliée par - 4pG.

On prend comme surface de Gauss une sphère de rayon r : sur cette sphère le champ de gravitation a une norme constante et est colinéaire au vecteur surface.

pour r supérieur au rayon de la répartition de masse, la somme des masses intérieures est m1.

g(r) 4pr² = -4pGm1.

g(r) = - Gm1/r²

Pour une répartition de matière à symétrie sphérique, le champ de gravitation à l'extérieur est identique à celui crée par un point matériel confondu avec le centre de la sphère.

D'après le principe des actions mutuelles la force qui s'exerce sur M1 est l'opposée de la force qui s'exerce sur M2. Le travail de ces deux forces est :

On peut trouver, par intégration, une fonction énergie potentielle telle que dW=- dEp

Ep = -Gm1m2 / r . cette énegie tend vers zéro si r tend vers l'infini.

définition du barycentre :

dériver par rapport au temps, utiliser la relation fondamentale de la dynamique pour chaque point

Le mouvement de G est donc un mouvement rectiligne uniforme. En conséquence, le référentiel barycentrique, en translation rectiligne uniforme par rapport au référentiel du laboratoire, est galiléen.

écrire la relation fondamentale de la dynamique pour chaque masse puis soustraire membre à membre

Le moment cinétique des deux masses s'écrit :

(1) est la définition du barycentre; dériver cette expression par rapport au temps pour obtenir (2)

La dernière expression du moment cinétique ne dépend plus de N.

La particule fictive de masse m subit une force centrale notée f2 de la part de G. La dérivée du moment cinétique par rapport au temps est nulle et le moment cinétique est constant.

Le moment cinétique est un invariant vectoriel et le mouvement est dans un plan contenant G ,orthogonal au moment cinétique.

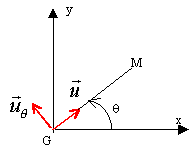
en coordonnées polaires le moment cinétique s'écrit :

l'invariance du moment cinétique conduit à : r² dq/dt=C

en notant dS l'aire balayée pendant la durée dt, la vitesse aérolaire est également une constante du mouvement:

dS/dt = ½r² dq/dt = ½C

expression de la loi des aires dont l'énoncé est le suivant :

dans un mouvementà force centrale,le rayon vecteur balaie des aires égales pendant des durées égales.

énergie cinétique dans le référentiel barycentrique :

Ec = ½m1v1² +½m2v2²

remplacer les vitesses par leurs expressions en fonction de v:

Ec = ½ m1(m2/(m1+m2))²v² + ½ m2(m1/(m1+m2))²v² = ½ mv².

en coordonnées polaire l'énergie cinétique s'écrit :

Ec= ½ m[r'² + r² q'²]

faire apparaître C = r²q'

Ec= ½ m[r'² + C²/r² ]

l'énergie mécanique est la somme de l'énergie cinétique et potentielle

E = ½ m[r'² + C²/r² ] -Gm1m2/r.

force gravitationnelle : 6,67 10-11*3,27 10-25* 6,65 10-27 / d² = 1,45 10-61 /d²

force de Coulomb : 9 109 *79 * (1,610-19)² / d² =1,82 10-26 /d²

force de coulomb / force de gravitation = 1,2 1035.

énergie du système : E = ½mv² + 2Ze² / (4pe0r)

retour - menu