Cinétique chimique : ordre de réaction ordres de réaction 0, 1 ou 2 : temps de demi-réaction méthode différentielle par spectrophotométrie En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .

ordres de réaction 0, 1 ou 2 : temps de demi-réaction Soit une réaction dont le bilan est : A-->B ; la vitesse de réaction s'écrit : v=k[A]a. a est l'ordre de la réaction, 0, 1 ou 2 ; k est la constante de vitesse. On note [A]0 la concentration initiale du réactif A. Pour chaque valeur de a : Comment déterminer graphiquement la constante de vitesse k. Quelle est son unité ? Quelle est la représentation de [R] en fonction du temps ? Déterminer le temps de demi-réaction . corrigé la vitesse de réaction s'écrit : v= -d[A] /dt la concentration [A] est solution de l'équation différentielle : -d[A] /dt =k[A]a. réaction d'ordre 0 : -d[A] /dt =k0. d'où [A]= -k0t + [A]0 droite de pente opposée à la constante de vitesse k0. k0 s'exprime en mol L-1 s-1. temps de demi-réaction t½ : durée au bout de laquelle la moitié du réactif limitant a été consommée. à t½ [A]=½[A]0 d'où ½[A]0 = -k0t ½ + [A]0 soit t ½ =[A]0 /(2k0). réaction d'ordre 1 : -d[A] /dt = k1[A] ; k1 s'exprime en s-1. d'où d[A] /[A]= -k1dt soit : ln[A] = -k1t +ln[A0] Tracer la courbe d'équation ln [A]= f(t) , droite de pente -k1. temps de demi-réaction t½ : ln(½[A0] )= -k1t ½ +ln[A0] ; t ½ =ln2 /k1. réaction d'ordre 2 : -d[A] /dt = k2[A]2 ; k1 s'exprime en L mol-1 s-1. d'où d[A] /[A]2= -k2dt soit : 1/[A] = k2t +1/[A0] Tracer la courbe d'équation 1/[A] = f(t) , droite de pente k2. temps de demi-réaction t½ : 1/(½[A0] )= k2t ½ +1/[A0] ; t ½ =1 /(k2[A0] ).

méthode différentielle   Considérons la réaction A-->B+C. La vitesse de réaction peut se mettre sous la forme v= k[A]a où a est un réel. L'évolution de la concentration du composé A et de la vitesse -d[A]/dt sont donnés dans le tableau ci-desous : t (min) 1 10 15 20 25 35 50 [A] mol/L 0,44 0,23 0,18 0,14 0,11 0,07 0,04 -d[A]/dt *104 (molL-1min-1) 6,3 2,6 1,6 1,1 0,8 0,5 0,25 Déterminer les grandeurs k et a. corrigé la concentration [A] est solution de l'équation différentielle : -d[A] /dt =k[A]a. soit ln (-d[A] /dt)=ln k + a ln[A], droite de coefficient directeur a et d'ordonnée à l'origine ln k. si a=0, réaction d'ordre zéro : -d[A] /dt doit être une constante, ce qui est contraire aux données du tableau. 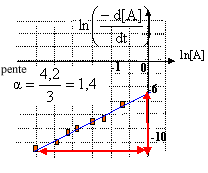t (min) 1 10 15 20 25 35 50 [A] mol/L 0,44 0,23 0,18 0,14 0,11 0,07 0,04 -d[A]/dt (molL-1min-1) 6,3 10-4 2,6 10-4 1,6 10-4 1,1 10-4 0,8 10-4 0,5 10-4 0,25 10-4 ln[A] -0,776 -1,386 -1,66 -1,9 -2,12 -2,53 -2,995 ln (-d[A] /dt) -7,38 -8,31 -8,73 -9,1 -9,42 -9,99 -10,68 l'ordonnée à l'origine est égale à -6,4 : ln k=-6,4 d'où k = 1,7 10-3 (mol L-1)1,4 -1 min-1.

par spectrophotométrie   Oxydation des ions iodures I- par les ions peroxodisulfates S2O82- en solution aqueuse. 2I-+S2O82- =I2 + 2SO42-. La réaction admet l'ordre partiel p par rapport aux ions iodures et un ordre partiel n par rapport à S2O82- . A la date t=0 on mélange 25 mL d'une solution d'iodure de potassium à 0,25 mol/L et 15 mL d'une solution de peroxodisulfate d'ammonium à 6,25 10-3 mol/L. Ces conditions initiales permettent de déterminer l'ordre n de la réaction.Justifier. Donner l'expression de la constante de vitesse apparente. On mesure l'absorbance du mélange au cours du temps. Seul le diiode formé est coloré donc responsable de l'absorbance. On rappelle la loi de Beer Lambert donnant l'absorbance A d'une solution de concentration c placée dans une cuve de longueur L : A=eALc avec eA le coefficient d'extinction molaire de la substance absorbante à la longueur d'onde l= 454 nm. A = 1250 L mol-1 cm-1. - Expliquer comment la mesure de l'absorbance permet de déterminer la concentration des ions peroxodisulfate au cours du temps. - On obtient les résultats suivants : t (min) 0 4 8 12 16 A 0 0,35 0,67 0,94 1,18 Montrer que ces résultats sont en accord avec une cinétique d'ordre n=1. Calculer la constante de vitesse apparente. corrigé à l'instant initial, on a introduit : 25 10-3*0,25 = 6,25 10-3 mol d'ion I- et 15 10-3*6,25 10-3 = 9,37 10-5 mol d'ion peroxodisulfate. Les ions iodures sont en grand excès et la concentration des ions iodures peut être considérée comme constante. La vitesse de la réaction s'écrit : v = k [I- ]p[S2O82-]n avec k la constante de vitesse. v = k' [S2O82-]n avec k' = k [I- ]p, constante de vitesse apparente. La réaction admet l'ordre partiel n par rapport aux ions peroxodisulfate. D'après la loi de Beer, la concentration en diiode [I2] est proportionnelle à l'absorbance A : [I2] = A/(eAL) = A/1250. 2I- +S2O82- =I2 + 2SO42- initial 6,25 10-3 mol 9,37 10-5 mol 0 0 en cours 6,25 10-3 -2x 9,37 10-5 -x x x fin 6,25 10-3 -2*9,37 10-5 0 9,37 10-5 9,37 10-5 qté de matière : nS2O82- = 9,37 10-5 -x = 9,37 10-5 -nI2; volume du mélange 0,04 L d'où : [S2O82- ]=9,37 10-5 /0,04 - [I2]= 2,34 10-3 -A/1250. si la cinétique est d'ordre 1, on trace ln[S2O82- ] en fonction du temps :on doit alors obtenir une droite dont la pente donne l'opposé de la constante de vitesse apparente k'. 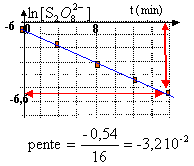t (min) 0 4 8 12 16 A 0 0,349 0,67 0,94 1,178 ln[S2O82- ] -0,605 -6,185 -6,44 -6,56 k' = 3,2 10-2 min-1. retour - menu