Concours GEP- 98 un choix d' exercices de physique (terminale)
				. .
exercice 1	glissière circulaire -chute- vitesse- accélération
Le mobile de masse m est laché de A sans vitesse. Il se déplace dans une glissière ABMC, sans frottements. Au dela de C, il n'est soumis qu'à son poids AB=h=1 m ; OB=r=50 cm; g=10 ms-2.
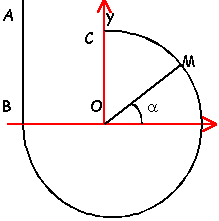
Quelle est la vitesse du mobile en C en ms-1 et km h-1. Donner l'équation de la trajectoire du mobile au dela de C Exprimer l'accélération du mobile en M en fonction de h, g, r et a.
..
corrigé
th de l'énergie cinétique entre A et C (l'origine des altitudes est celle du point O ) ou bien on écrit que l'énergie mécanique se conserve. l'altitude de C doit être inférieure à celle de A, sinon C n'est pas atteint (on part sans vitesse de A) Energie mécanique en A = énergie potentielle = mgh Energie mécanique en C = 0,5 mV²C + mg R V²C =2g(h-r) = 2*10(1-0,5)= 10 VC=3,16 ms-1=3,16*3,6 km h-1 au dela de C, chute libre, le solide n'est soumis qu'à son poids. expression de la vitesse en M : conservation de l'énergie mécanique entre A et M: mgh = 0,5 mV²M + mg r sin(a) V²M =2g(h-r sin(a)) accélération normale du mobile en M aN =V²M/rayon = 2g(h/r-sin(a)) accélération normale du mobile en M écrire la seconde loi de newton suivant un axe colinéaire à la vitesse et de même sens aT= -gcos(a)				dans le repère proposé origine des temps: le passage en C accélération (0; -10) vitesse en C (-3,16 ; 0) position OC (0; 0,5) vitesse à la date t ( -3,16; -10 t ) position à la date t-3,x=-3,16t y=-5t²+0,5 trajectoire y= -5/3,16² x²+0,5
exercice2	l'horloge entretenue.
Une horloge est constituée d'un pendule simple entretenu de période propre 2 s. Pour maintenir l'amplitude des oscillations constante, l'horloge puise son énergie dans l'énergie potentielle d'une masse de 1 kg descendant d'une hauteur de 1 m par semaine. g=9,8 m s-2. longueur du pendule l= 1 m. Evaluer le travail des frottements au cours d'une oscillation. La longueur d'un pendule simple peut varier avec la température. Quel est l'allongement Dl acceptable pour que l'horloge indique encore l'heure exacte à 10 secondes près au bout d'un jour de fonctionnement.
..
corrigé
Energie potentielle stockée par cette masse : m g h =1* 9,8 *1 = 9,8 J une semaine =7*24*3600=604 800 s ou 302 400 oscillations travail des frottements = opposé de l'énergie utilisée à chaque période pour entretenir le pendule - 9,8/ 302 400= 3,24 10-5 J période du pendule simple dérivée logarithmique de la période DT/T=10/(24*3600)=1,157 10-4 ; Dl =2*1,157 10-4 = 2,3 10-4 m
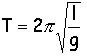
exercice 3	résonance- circuit RLC- puissance
Un dipole RLC (C=10-9 F ; L=1 H ) est alimenté par une tension u(t)=10cos(wt) Quelle est la fréquence propre du dipole ? Lorsque la fréquence du générateur est égale à la fréquence propre, la valeur maximale de l'intensité est 1 mA. Quelle est la résistance du circuit ? Le facteur de qualité est Q=4,45. En déduire la bande passante. Quelle est la puissance P0 fournie au dipole par le générateur à la fréquence propre. A une fréquence supérieure à la fréquence propre, comparer la puissance moyenne P fournie au circuit à P0.
..
corrigé
fréquence propre f0= 1/ T= 5035 Hz La fréquence du générateur est égale à la fréquence propre : phénomène de résonance d'intensité. L'intensité efficace passe par une valeur maxi et l'impédance du circuit par une valeur minimale , égale à la résistance . R=Umax / I max= 10/0,001 =104 ohms Q=f0 /Df ; Df = 5035/4,45 = 1131 Hz puissance consommée P=U eff Ieff cos(j) à la résonance tension et intensité sont en phase cos(j)=1 ; Uefficace=U maxi/1,414 ; Iefficace=Imaximale / 1,414 P=10/1,414*10-3/1,414= 5 milliwatts sinon l'intensité efficace est inférieure à 1 mA de plus tension et intensité sont décalées (déphasées) cos(j)<1 donc la puissance consommée est inférieure à 5 mW
..
exercice 4	balle et rebond
Une balle de masse m=100g est lachée sans vitesse d'une hauteur h=1 m. g=9,8 ms-2. La balle rebondit sur le sol. L'énergie cinétique juste après le rebond est égale à l'énergie cinétique juste avant multipliée par une constante k=0,9. Quelle est la vitesse de la balle juste après un rebond ? Quelle est l'altitude maxi atteinte après un rebond ? Quelle est la durée de la seconde descente ? Reprendre les deux questions précédentes mais après le 5 ème rebond.
.
corrigé
juste avant le premier rebond l'énergie potentielle initiale est sous forme cinétique 0,5 mv²=mgh =0,1*1*9,8=0,98 J juste après le premier rebond l'énergie cinétique vaut 0,98*0,9= 0,882 J d'où la vitesse après rebond: v²=0,882*2/0,1 ; v=4,2 ms-1. à l'altitude maximale après rebond l'énergie se trouve sous forme potentielle. 0,882=mg h' ; h'=0,882/(0,1*9,8)= 0,9 m durée de la chute libre lors de la seconde descente h'=0,5*9,8 t² ; t²=0,9/4,9 ; temps =0,428 s au dela du 5 ème rebond énergie cinétique juste aprés ce 5ème rebond = E initiale fois 0,95. 0,98*0,95=0,578 J d'où la vitesse v²=0,578*2/0,1=11,56 ; v=3,4 ms-1. altitude= altitude de départ *0,9 5 = 0,59 m ou bien 0,578=mgh durée: 0,59=0,5*9,8 t² ; t=0,346 s
exercice 5	trois charges électriques sur un axe
Soit la distribution de charges (microcoulombs) ci contre ;AB=d= 0,2 m ; Les deux charges placées en A et B sont fixes; par contre la charge placée en C est mobile sur la droite AB.
Quelle est la position d'équilibre de la charge placée en C, si elle existe ?
..
corrigé
Les charges placée en A et C sont de signe contraire: elles s'attirent .La force attractive a pour valeur: 9 10-9 *|2q|*|-q|/AC²=9 10-9 *2q2/x² avec AC=x Les charges placée en B et C sont de signe contraire: elles s'attirent .La force attractive a pour valeur: 9 10-9 *|q|*|-q|/BC²=9 10-9 *q2/(d-x)² La charge placée en C est soumises à 2 forces électriques: il y a équilibre si ces forces sont opposées. Ce qui n'est possible que si C est entre A et B. 9 10-9 *2q2/x²=9 10-9 *q2/(d-x)² 2q2/x²= q2/(d-x)² 2/x²=1/ (d-x)² avec d=0,2 la résolution de l'équation du second degré donne: x=0,117 m
		..
exercice 6	pendule conique
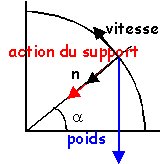
Une masse m=0,1 kg ponctuelle est attachée à un fil inextensible de longueur l=1 m. La masse tourne autour de la tige et l'angle a est constant a=22,5° ; g=9,8 ms-2 .
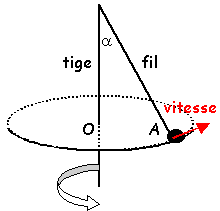
Quelle est la vitesse angulaire w en rad s-1 ? Quelle est la tension du fil ? Quelle est la valeur de la vitesse v ? Pour quelle valeur minimale de w le fil commence t-il à se détacher de la tige verticale ?
.
corrigé
L'accélération est centripète dirigée vers O de valeur aN =v²/OA = w²*OA avec OA=l sin(a) tan(a)= m aN / mg voir schéma ci contre tan(22,5)= w² sin(22,5)/9,8 ou bien 1/cos(a)= w²/9,8 ou bien w²=9,8 / cos(22,5)=10,6 ; w=3,26 rad s-1.
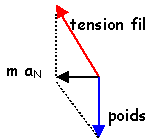
tension du fil T= mg/cos(a) = 0,1*9,8/cos(22,5)= 1,06 N vitesse de A v=w*OA=w*l sin(a)= 3,26*sin(22,5)= 1,25 ms-1. valeur minimale de la vitesse angulaire cos(a)=9,8/ w² voir ci dessus Lorsque le fil commence à se détacher de la tige verticale , l'angle vaut encore 0 et cos(0)=1 d'où la valeur minimale de la vitesse angulaire : w²=1/9,8 ; wminimale=3,13 rad s-1.
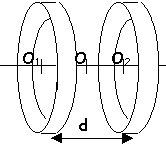
exercice 7	bobines de Helmholtz- champ magnétique uniforme
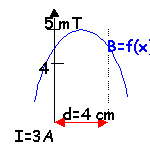
Deux bobines circulaires coaxiales de rayon R=6,5 cm sont parcourues par un courant d'intensité I=3 A. Chaque bobine compte N=100 spires. On cherche à obtenir en O, milieu de O1O2 un champ magnétique uniforme. Le courant dans les deux bobines a t-il le même sens ? Comparer d et le rayon R des bobines lorsque le champ est uniforme en O. Quelle est la bonne expression de B champ magnétique crée en O (k est sans unité ; m0= T m A-1) km0N/(RI) km0NI/R km0NIR Calculer B si k=0,71
corrigé
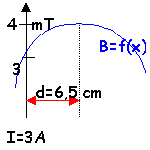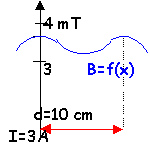
Les courants doivent avoir le même sens: dans ce cas les champs magnétiques crées par les bobines en O s'ajoutent. Avec des courants de sens contraire les champs en O vont s'annuler. La distance d doit avoir une valeur voisine du rayon R des bobines. B est en tesla T ; m0 est en T m A-1 il faut donc multiplier m0 par des ampères et divisé par une longueur km0NI / R Calcul de B 0,71*100*3*4p10-7/6,5 10-2= 4,1 mT
exercice 8	identifier un dipole
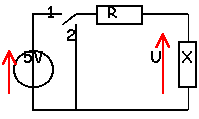
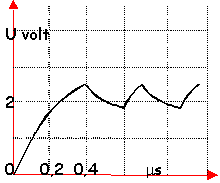
A la date t=0 on ferme l'interrupteur en position 1. A la date t1 l'interrupteur bascule en position 2. A la date t2 l'interrupteur bascule en position 1 et ainsi de suite. On relève la courbe donnant la tension U aux bornes du dipole inconnu X au cours du temps. Identifier X et calculer la constante de temps du circuit. Si R=1000 ohms en déduire la grandeur caractéristique du dipole X.
..
corrigé
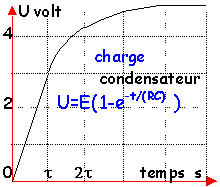
L'allure des courbes entre 0 et t1 indique que X est un condensateur en train de se charger. A t=0,4 ms U=2,5 V lecture graphe 2,5=5(1-e-0,4/t) avec t=RC en microsecondes 2,5/5=0,5 = 1-e(-0,4/t) 0,5=e(-4/t) -0,4/t =ln(0,5)=-0,693 constante de temps: 0,4/0,693= 0,47 microsecondes 0,47 10-6=1000*C C=0,47 10-9 F
exercice 9	relais 4x400m
Un coureur X arrive avec un mouvement uniforme v=7,5 ms-1. A 10 m devant lui, le coureur Y s'élance d'un mouvement uniformèment accéléré a=2 ms-2. Quel temps s'écoule entre le moment où Y démarre et le passage du témoin. Pendant cette durée quelles sont les distances parcourues par X et Y. Tous les coureurs ont une accélération de 2 ms-2 jusqu'à atteindre une vitesse v= 7,5 ms-1 qu'il conserve jusqu'au passage du témoin. Les passages du témoin se font tous les 400 m. Quelle est la durée de la course ?
.
corrigé
origine des temps: t=0 au démarrage de Y origine des abscisses: position de Y à t=0 équations horaires: coureur X: x=7,5t-10 coureur Y: x=t² tant que la vitesse est inférieure à 7,5 ms-2.  passage du témoin : les deux coureurs se rejoignent 7,5t-10 = t² la résolution donne t=1,73 s la seconde solution t=5,77 s :si X continue à courir à la même vitesse , il va rattraper Y distance parcurue par X en 1 ,73 s à la vitesse de 7,5 ms-1, en 1,73 s X parcourt une distance de :1,73*7,5= 13 m le premier coureur démarre avec une vitesse nulle: mouvement uniformément accéléré jusqu' à atteindre la vitesse de 7,5 ms-1 puis mouvement uniforme x=t² donc v= 2t ; t=7,5/2= 3,75 s durée du mvt accéléré. il a parcouru: x=3,75²= 14,06 m il lui reste a parcourir 400-14,06 = 385,94 m à la vitesse de 7,5 ms-1. La durée de ce mvt est 385,94/7,5=51,46 s soit au total la course du premier dure: 55,2 s. au passage du témoin quelle est la vitesse du second ? 3 m parcourus: 3=0,5 *2*t² ; t=1,732 s ; v=2t=3,46 ms-1 il lui reste à parcourir 400 m avant de rattraper le 3 ème. mvt uniformèment accéléré jusqu' à atteindre la vitesse de 7,5 ms-1 puis mouvement uniforme on ne change pas les origines définies ci dessus. x=0,5*2*(t-55,2)²+3,46 (t-55,2) +400 v=2((t-55,2)+3,46 =7,5 d'où t=55,2+2,02=57,2 s durée de l'accélération 2,02 s la distance parcourue est: x-400=2,02²+3,46*2,02=11,06 m il lui reste à parcourir 400-11,06=388,94 m à la vitesse de 7,5 ms-1 durée =51,85 s durée de la course du second (et du 3 ème):51,85+2,02=53,87s par contre le dernier parcourt 385,94 m à la vitesse de 7,5 ms-1 durée 51,46s total: 216,4s
exercice 10	chute libre avec frottements - vitesse limite
Une balle de golf est lachée sans vitesse initiale en O, origine d'un axe orienté vers le bas. La résistance de l'air est proportionnelle au carré de la vitesse. Ecrire la 2ème loi de Newton et en déduire une relation entre v, v' dérivée de la vitesse par rapport au temps. Ecrire cette relation sous la forme v' = g(1-a²v²) (1) Quelle est l'unité de a ? Les maths proposent une solution de l'équation différentielle ci dessus: Quelle est la vitesse limite si a=0,02857?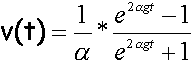 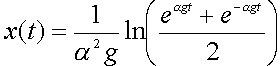Quelle distance parcourt la balle pour atteindre cette vitesse ? Comparer ce résultat à celui d'une chute libre. La vitesse limite est atteinte si t=10s.
..
corrigé
la balle est soumise à deux forces: le poids verticale vers le bas et la résistance de l'air , verticale vers le haut. mg-kv²=ma avec a=v' g - k/m v²= v' g( 1-k/ (mg) v²)=v' avec a² =k / (mg) a²v² est sans unité car ce terme est retranché à 1. a est donc l'inverse d'une vitesse si le temps devient grand, supérieur à 10 s par exemple: e 2agt-1 est équivalent à e 2agt e 2agt+1 est équivalent à e 2agt la vitesse limite vaut 1/a =35ms-1. distance parcourue remplacer chaque grandeur par sa valeur numérique dans x(t) 264 m dans le cas d'une chute libre sans vitesse initiale x(t)=0,5 gt² 0,5*9,8*10²=490 m
retour - menu