Ondes : physique concours FESIC 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

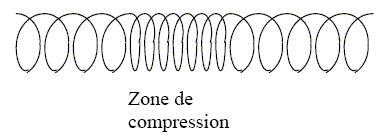
Répondre par vrai ou faux. L’extrémité d’un ressort à spires non jointives, considéré infiniment long, est comprimée, puis relâchée brusquement au temps t0 = 0. Une onde se propage alors le long du ressort. A- C’est une onde mécanique progressive. Vrai. B- L’onde est une onde transversale. Faux. Onde longitudinale : la direction de la variation de pression est identique à la direction de propagation de l'onde. C- La célérité c de l’onde est constante au cours de la propagation. Vrai. Au tems t1 la célérité a pour valeur c = 15 m/s. D- Au temps t1 = 10,0 ms, la zone de compression se situe à la distance d = 150 m de l’origine. Faux. d = c t1 = 15*0,01 = 0,15 m. Un faisceau de lumière parallèle monochromatique, de longueur d'onde l = 600 nm, produit par une source laser, arrive sur une fente de largeur a = 0,10 mm. On place un écran perpendiculairement à la direction du faisceau a une distance D = 2,0 m de la fente. 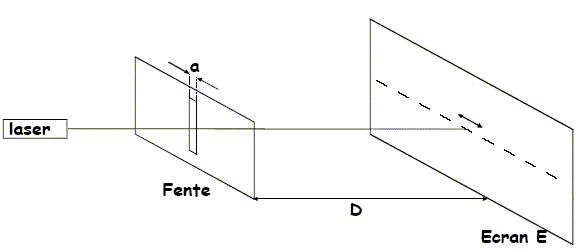A-La fréquence de l’onde lumineuse émise par ce laser est 5,00 1014 Hz. Vrai. l = 600 nm = 600 10-9 m = 6,00 10-7 m ; f = c/l = 3,00 108 / 6,00 10-7 =5,00 1014 Hz. B- L’écart angulaire entre le milieu de la tache centrale et la première extinction est donné par la relation q = a/l. Faux. 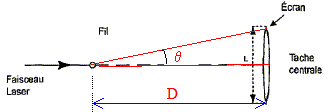q = l/a avec : l longueur d'onde (m) et a : diamètre du fil ou largeur de la fente (m) C- La largeur de la tache centrale est de 1,2 cm. Faux. tan q = ½L/D voisin de q radian pour les angles petits. en tenant compte des deux relations ci-dessus : ½L/D=l/a soit L = 2l D/a. L = 2* 6,00 10-7*2,0 / 10-4 =2,4 10-2 m = 2,4 cm. D- Lorsque cette onde lumineuse se propage dans de l’eau (indice de réfraction 1,33), la fréquence de cette onde ne change pas. Vrai.   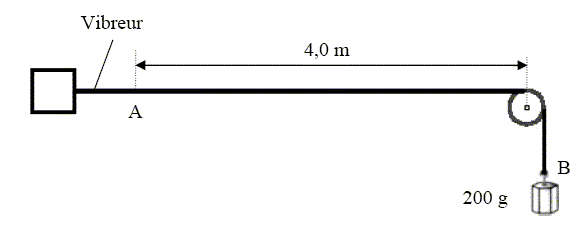Web www.chimix.com On attache une masse de 200 g à l’extrémité B d'une corde maintenue horizontale sur sa plus grande longueur, puis on produit une déformation sinusoïdale, de fréquence 100 Hz, à l’extrémité A de la corde, grâce à un vibreur. La célérité des ondes le long de la corde est donnée par la relation : v = (T/m)½. T est la tension de la corde et m= 20 g m-1, la masse linéique de la corde. On prendra : g = 10 N.kg-1 et on admettra que la valeur de la tension de la corde est égale au poids de la masse suspendue. A- La tension peut s’exprimer en kg.m.s-1. Faux. force = masse * accélération = masse *longueur / temps2 ; [tension] =M L T-2. B- La célérité de l’onde augmente avec la masse linéique de la corde. Faux. v = (T/m)½ ; la célérité diminue si la masse linéique augmente. C- La corde est le siège d’oscillations forcées. Vrai. Une corde tendue entre deux points fixes et soumise à une excitation sinusoïdale entre en résonance lorsque les fréquences excitatrices sont multiples d'une même fréquence f0, appelé mode fondamental. On peut observer la formation d'ondes stationaires. D- La valeur de la longueur d’onde est l =10 cm. Vrai. T = mg = 0,2*10 = 2 N ; m = 20 g m-1 = 0,020 kg m-1 ; v = [2/0,02]½ =10 m/s. f = 100 Hz ; l =v /f = 10 / 100 = 0,10 m = 10 cm. Une corde horizontale, supposée infinie, est soumise à un ébranlement transversal sinusoïdal à partir de son extrémité O. L’origine des temps est prise lorsque O passe par sa position d’équilibre en allant vers le haut. Sa fréquence est de 100 Hz et son amplitude de 1 mm . Il se propage dans le sens positif, de la gauche vers la droite, avec une célérité de 5 m.s-1. Les amplitudes y sont exprimées en mm. A- L’équation horaire du point O est y (t ) = sin (200 pi t). Vrai. B- L’équation horaire du point N1 situé 5 cm à droite de O est y (t ) = sin (200 pi t). Vrai. longueur d'onde l = v/f =5 /100 = 5 cm ; les point N1 et O, distants d'un nombre entier de longueur d'onde vibrent en phase. C- L’équation horaire du point N2 situé 2,5 cm à droite de O est y (t ) = -sin (200 pi t). Vrai. Les point N2 et O, distants d'une demi-longueur d'onde vibrent en opposition de phase. D- A l’instant t = 0 , la corde est représentée par la courbe y (x) = sin (40pi x). Faux. y(0, x) = sin [200 pi (t-x/v) ]=sin [200 pi t-200 pi x/v ]. y(0, x) = sin [200 pi *0 - 200 pi x/5 ] =sin( -40 pi x) = -sin (40 pi x) E- A l’instant t = 5 ms , la corde est représentée par la courbe y (x) = -sin (200 pi x). Faux. y(5 10-3, x) = sin [200 pi (t-x/v) ]=sin [200 pi t-200 pi x/v ]. y(5 10-3, x) = sin [200 pi *5 10-3 - 200 pi x/5 ] =sin( pi -40 pi x) = sin (40 pi x)

retour -menu