Physique et raccordement routier, Bac Amérique du Nord 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Lors de la création d’un nouveau raccordement routier, les ingénieurs en génie civil doivent déterminer la trajectoire la plus sûre pour les usagers. La réussite de leur travail tient alors beaucoup à une courbe plane remarquable appelée clothoïde  qui permet de raccorder une ligne droite à un cercle. Ce raccordement permet de réduire les risques en assurant une augmentation linéaire dans le temps de l’accélération jusqu’à une valeur constante et maximale dans l’arc de cercle. 1. Mouvement sur l’arc de clothoïde (entre O et S).  La partie OP de l’échangeur au début de l’arc de clothoïde est considérée comme une ligne droite horizontale. Q.1. Déterminer la valeur de l’accélération du véhicule sur la portion OP à partir de la figure 2 et caractériser le mouvement du véhicule. 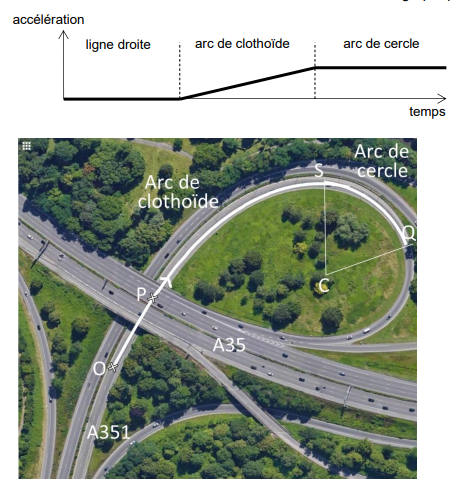Accélération nulle, donc vitesse constante et mouvement rectiligne. Donc mouvement rectiligne uniforme.  On s’intéresse à un véhicule parcourant la trajectoire plane et horizontale entre O et S. Ce véhicule est assimilé à un point matériel M, d’accélération initiale nulle et animé d’une vitesse de norme constante v égale à 15,0 m·s-1 . Ses coordonnées x et y, prises à intervalle de temps régulier, sont introduites dans le programme Python ci-dessous : Les valeurs successives de la norme de l’accélération du véhicule calculées à l’aide du programme figurent dans le tableau suivant : t(s) 1,50 3,00 4,50 6,00 7,50 9,00 a ( m s-2) 0,1587 0,3218 0,4824 0,6411 0,8070 0,9506 a ( m s-2) / t(s) 0,1058 0,1073 0,1072 0,1069 0,1076 0,1056 Sur la copie, écrire les lignes de programme permettant de calculer les coordonnées ax et ay du vecteur accélération. ax  : variation de la composante de la vitesse selon l'axe Ox /  durée de cette variation. ay  : variation de la composante de la vitesse selon l'axe Ox /  durée de cette variation. Lignes 11 et 12. Q.3. À l’aide des valeurs données dans le tableau, vérifier l’information du texte introductif indiquant que la clothoïde permet « une augmentation linéaire dans le temps de l’accélération » en justifiant la méthode utilisée. a ( m s-2) / t(s) est constant. ( voit ligne 3 du tableau ). ... .... 2. Mouvement sur l’arc de cercle (entre S et Q).  Le véhicule, assimilé à un point matériel M, poursuit sa trajectoire en décrivant l’arc de cercle, de rayon r = 75,0 m, entre les points S et Q. La norme de la vitesse garde une valeur constante v égale à 15,0 m·s-1 . Q.4. Sur le schéma de l’Annexe à rendre avec la copie (page 14), tracer les vecteurs unitaires uN et uT du repère de Frenet au point M de la trajectoire en arc de cercle. 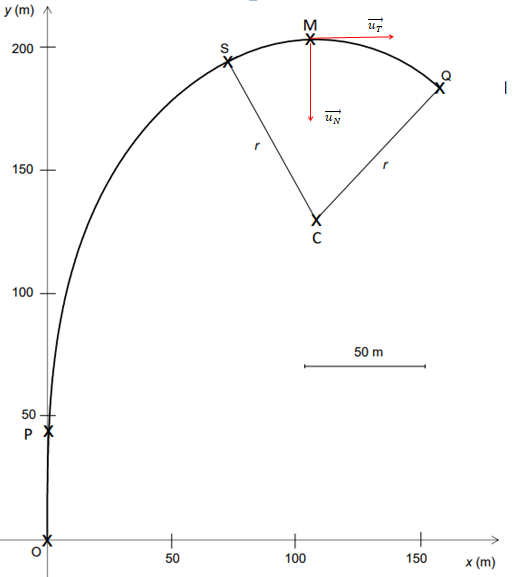Q.5. 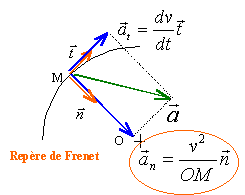Justifier que le vecteur accélération du véhicule entre les points S et Q s’exprime ainsi :  Q.6. Sur le schéma de l’Annexe à rendre avec la copie , représenter à l’échelle 1,0 cm pour 1,0 m·s-2 , le vecteur accélération a au point M. aT = 0, le mouvement étant uniforme. aN = v2 / R =152 / 75=3 ms-2. 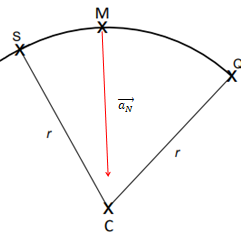Un véhicule immobile sur une route est soumis à deux actions mécaniques, modélisées par son poids P et la réaction R exercée par la chaussée. En mouvement uniforme dans un virage, le véhicule est aussi soumis à une action, modélisée par une force f appelée force de frottement. Les forces qui s’appliquent au véhicule sont contenues dans le plan vertical perpendiculaire à la route. Le point C est le centre de la trajectoire circulaire. Le véhicule est assimilé au point M. Les cinq schémas suivants représentent le poids P , la réaction R et la force de frottement f . 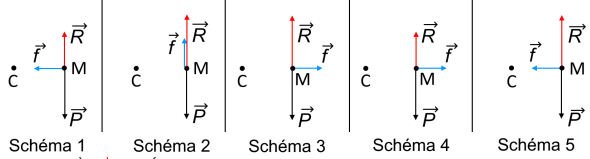Q.7. Indiquer, en justifiant, le numéro du schéma qui représente correctement ces trois forces, en s’appuyant sur les caractéristiques du vecteur accélération. Le mouvement étant uniforme, la composante tangentielle de l'accélération est nulle. Les schémas 1 et 4 ne conviennent pas. La composante normale de l'accélération étant dirigée vers C, le schéma 5 convient. Dans la pratique, la sécurité dans les virages dépend aussi de la qualité des pneus, de la suspension des roues et de l'adhérence de la chaussée. Pour un véhicule de masse 1 200 kg, la valeur de la force de frottement ne peut pas dépasser 10 400 N sur chaussée sèche et 7 200 N sur chaussée humide. Si ces valeurs sont atteintes alors l’adhérence à la route n’est plus assurée et le véhicule dérape. Q.8. Dans le cas du virage étudié précédemment, choisir parmi les panneaux de limitations de vitesse 50, 70, 90 110 quel est celui qui devrait être placé avant le point O. Expliquer le raisonnement. Cas le plus défavorable : chaussée humide  f = 7200 N. r = 75,0 m. aN = f / m =7200 / 1200 =6 m s-2. v2 = r aN =75 x6 =450 v max =21,2 m/s ou 21,2 x 3,6~76 km/h. Panneau limitant la vitesse à 70 km / h.

menu