Raven
Saunders, la lanceuse de poids américaine, Bac
Amérique du Nord
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Le
poids est une sphère métallique de masse m. Le lanceur est dans l'aire
de lancement délimitée par un cercle métallique et par un butoir. La
portée du jet D est mesurée du butoir B au point de chute M.
A l'issue de la phase d'élan, le poids est abandonné en A, à la hauteur
OA = h au dessus du sol horizontal, à la distance BO du butoir. Le bras
qui lance fait un angle a avec l'horizontale. Cet angle est considéré comme étant celui de la direction de la vitesse initiale v0 = 12,8 m/s.
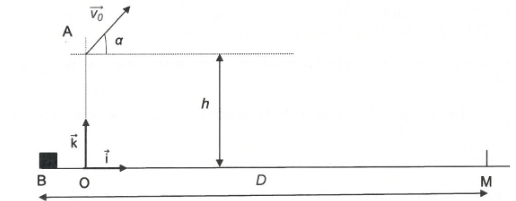
m=4,00 kg ; D = 18,62 m ; BO = 0,30 m ; OA=h=1,80 m ; a = 45,0° ; g = 9,81 m s-2.
Force de frottement exercée par l'air : f =½r Cx S v2.
S = 7,62 10-3 m2 ; r = 1,29 kg m-3 ; Cx =0,51 ; v : vitesse maximale v = 14 m/s.
Q1. Montrer que la valeur de f est très petite devant la valeur du poids.
f = 0,5 x1,29 x0,51 x 7,62 10-3 x 142 =0,49 N.
P = mg = 4,0 x9,81 ~39 N, soit 80 fois plus grande que f.
Q2. Montrer que les équations horaires du mouvement de la sphère sont :
accélération : ax =0 ; az = -g.
vitesse : vx = v0 cos a ; vz = -gt +v0 sin a.
position : x = v0 cos a t ;
z = -½gt2+ v0 sin a t +h.
Q.3. Montrer que l'expression de l'équation de la trajectoire est :
t = x /( v0 cos a ) ; repport dans z :
z = -½gx2 /( v0 cos a )2+ v0 x tan a +h.
Q4. Montrer que l'abscisse du point de chute vaut x = 18,32 m.
OM = BM-BO =18,62 -0,30 = 18,32 m.
Q.5. Vérifier que la durée tM du déplacement de la sphère entre A et M est d'environ 2 s.
xM = v0 cos a tM ; tM = 18,32 /(12,8 x cos45) ~ 2 s.
Q6. En déduire la valeur vM de la vitesse au moment du contact avec le sol.
vx =12,8 cos 45 =9,05 m/s ; vz = -9,81 x2 +12,8 sin 45 =-10,57 m/s.
v2 = 9,052 +(-10,57)2 =193,6 ; vM =13,9 m /s~14 m/s.
Q7.
L'origine des énergies potentielles est fixée au niveau du sol
horizontal. Exprimer l'énergie mécanique de la sphère au moment du
lancer.
Energie cinétique :½mv02.
Energie potentielle : mgh.
Energie mécanique : ½mv02 +mgh.
Q8. En déduire l'expression de la vitesse vM au point de chute. La calculer.
Energie mécanique finale en M :½mvM2 .
Conservation de l'énergie mécanique :
½mvM2 =½mv02 +mgh.
vM2 =v02 +2gh.
vM2 =12,82 +2*9,81 x1,8 =199,156.
vM ~14 m/s.
|
|