Géométrie,
fonction. Bac
Amérique du Nord
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 3 QCM. 4 points.
L’espace est rapporté à un repère orthonormé.
On considère la droite (d) dont une représentation paramétrique est :
x = 3−2t
; y = −1
; z = 2−6t
, où t est un réel.
On considère également les points suivants : A(3 ; −3 ; −2)
; B(5 ; −4 ; −1) ; C le point de la droite (d) d’abscisse 2.
3-2t=2 ; t = 0,5 ; C(2 ;-1 ; -1).
H le projeté orthogonal du point B sur le plan P d’équation x +3z −7 = 0.
Affirmation 1
La droite (d) et l’axe des ordonnées sont deux droites non coplanaires. Vrai.
Vecteur directeur de la droite (d) : -2 ; 0 ; -6).
L'axe des ordonnées de vecteur directeur: (0 ; 1 ; 0) passe par l'origine du repère.
Représentation paramétrique de cet axe : x=0 ; y = 0+s ; z = 0 avec s réel.
Les deux droites ont des vecteurs directeurs non colinéaires, donc les deux droites ne sont ni parallèles ni confondues.
(d) et l'axe des ordonnées seront coplanaires si ces deux droites sont sécantes.
3t+2 = 0 soit t = 1,5 ;
-1 = s ;
2-6t = 0 soit t =0,5 ce qui est impossible.
Les deux droites ne possèdent pas de point commun..
Ces droites ne sont ni parallèles, ni confondues, ni sécantes : elles sont donc non coplanaires.
Affirmation 2
Le plan P passant par A et orthogonal à la droite (d) a pour équation cartésienne :
x +3z +3 = 0. Vrai.
Vecteur directeur de la droite (d) :( -2 ; 0 ; -6).
Vecteur orthogonal au plan P : (-2 ; 0 ; -6).
Equation de ce plan :-2x-6z+d=0.
A(3 ; −3 ; −2) appartient à ce plan : -2xA-6zA+d =0 ; -6+12+d=0 ; d = -6.
Equation de ce plan :-2x-6z-6=0.
Soit : x +3z +3 =0.
Affirmation 3.
Une mesure, exprimée en radian, de l’angle géométrique BAC est p /
6
.
Faux.
On étudie le produit scalaire suivant :
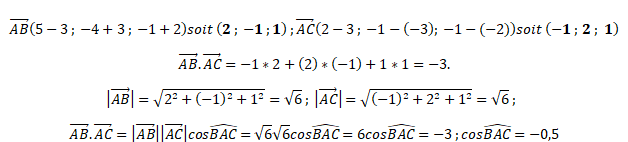
Cet angle mesure 2p /3.
Affirmation 4
La distance BH est égale à:
10½ /
2
. Vrai.
H le projeté orthogonal du point B(5 ; −4 ; −1) sur le plan P d’équation x +3z −7 = 0.
H est l'intersection du plan P et de la droite D orthogonale au plan P passant par le point B.
Vecteur directeur de la droite D : (1 ; 0 ; 3).
Représentation paramétrique de la droite D : x = t+xB = t+5.
y =0+yB = -4 ; z = 3t-1 avec t réel.
Intersection entre le plan P et la droite D :
t+5+9t-3-7=0 ; t=0,5=
H(0,5+5 ; -4 ; 3*0,5-1) soit H(5,5 ; -4 ; 0,5).
BH2 =(5,5-5)2 +(-4-(-4))2+(0,5-(-1))2 =0,25+2,25=2,5 =10/4 ; BH = 10½ /2.
|
...
|
....
|
Exercice 4 5 points.
La partie C est indépendante des parties A et B.
Partie A
On donne ci-dessous, dans un repère orthogonal, les courbes C1 et C2,
représentations
graphiques de deux fonctions définies et dérivables sur R. L’une des
deux fonctions représentées est la fonction dérivée de l’autre. On les
notera g et g
′
.
On précise également que :
- La courbe C1 coupe l’axe des ordonnées au point de coordonnées (0 ; 1).
- La courbe C2 coupe l’axe des ordonnées au point de coordonnées (0 ; 2) et l’axe
des abscisses aux points de coordonnées (−2 ; 0) et (1 ; 0).
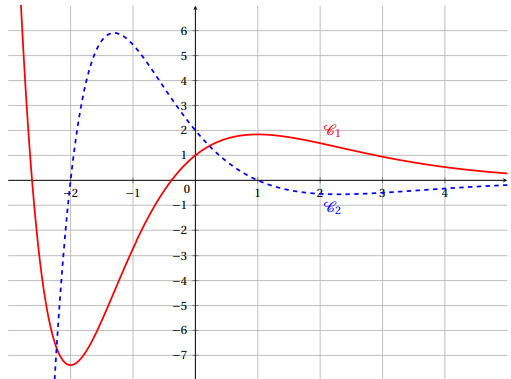
1. En justifiant, associer à chacune des fonctions g et g
′
sa représentation graphique.
C2 : dérivée g' ; C1 fonction g.
Quand la dérivée est négative ]-oo ; -2[ et ]1 ; +oo[, g(x) est décroissante.
Quand la dérivée est positive ]-2 ; 1(, g(x) est croissante.
Quand la dérivée s'annule ( x = -2) et x = 1) g(x) présente un extrémum.
2. Justifier que l’équation réduite de la tangente à la courbe représentative de la fonction g au point d’abscisse 0 est y = 2x +1.
Equation réduite de la tangente en x=0 : y = g'(0) (x-0) +g(0)
g(0) = 1 ; g'(0) = 2.
y =2x+1.
Partie B
On considère (E) l’équation différentielle
y + y
′ = (2x +3)e−x
,
où y est une fonction de la variable réelle x.
1. Montrer que la fonction f0 définie pour tout nombre réel x par f0(x) =(
x
2 +3x )
e
−x
est une solution particulière de l’équation différentielle (E).
Calcul de la dérivée en posant u =
x
2 +3x ; v = e-x ; u' = 2x+3 ; v'= -e-x.
u'v+v'u = (2x+3-x2-3x)e-x =(-x+3-x2)e-x.
Repport dans (E) : (
x
2 +3x -x+3-x2)e-x= (2x +3)e−x .
2. Résoudre l’équation différentielle (E0) : y + y
′ = 0.
y = A exp(-x) avec A une constante réelle.
3. Déterminer les solutions de l’équation différentielle (E).
y = (
x
2 +3x + A)
e
−x.
4. On admet que la fonction g décrite dans la partie A est une solution de l’équation
différentielle (E).
Déterminer alors l’expression de la fonction g.
g(0) = 1 =A.
g(x) = (
x
2 +3x + 1)
e
−x.
5. Déterminer les solutions de l’équation différentielle (E) dont la courbe admet exactement deux points d’inflexion.
Calcul de la dérivée première : u = x2+3x+B ; v = e-x.
u' = 2x+3 ; v' = -e-x.
u'v+v'u = (2x+3-x2-3x-B)e-x =-(x2+x+B-3)e-x.
Calcul de la dérivée seconde : u = x2+x+B-3 ; v = -e-x.
u' = 2x+1 ; v' = e-x.
u'v+v'u = (-2x-1+x2+x+B-3) e-x= (x2-x+B-4)e-x.
e-x est strictement positif ;
La signe de la dérivée seconde dépend du signe de x2-x+B-4.
Ce polynôme du second degré change de signe si et seulement si son discriminant est strictement positif.
D = (-1)2 -4(B-4) =17-4 B ; B < 17 /4.
La dérivée seconde s'annule et change de signe pour x=0. et x = 1.
Les solutions de l’équation différentielle (E) dont la courbe admet
exactement deux points d’inflexion sont des fonctions de la forme :
f(x) = (
x
2 +3x + C)
e
−x avec C < 17 /4.
Partie C
On considère la fonction f définie pour tout nombre réel x par :
f (x) = (
x
2 +3x +2 )
e
−x
1. Démontrer que la limite de la fonction f en +∞ est égale à 0.
On admet par ailleurs que la limite de la fonction f en −∞ est égale à +∞.
En plus l'infini, e-x tend vers zéro et
x
2 +3x +2 tend vers ^lus l'infini.
Par produit des limites, f(x) tend vers zéro si x tend vers +oo..
2. On admet que la fonction f est dérivable sur R. On note f
′
la fonction dérivée de
f sur R.
a. Vérifier que, pour tout nombre réel x,
f
′
(x) = (
−x
2 − x +1)
e
−x
.
On pose u = x2+3x+2 et v = e-x.
u' = 2x+3 ; v' = -e-x.
u'v+v'u = (2x+3-x2-3x-2)e-x = (-x2-x+1)e-x.
b. Déterminer le signe de la fonction dérivée f
′
sur R puis en déduire les variations de la fonction f sur R.
e-x est strictement positive.
Le signe de la dérivée est celui de -x2-x+1.
D = 1+4=5.
Solutions : x1 = (-1+5½) / 2 et x2 =(-1-5½) / 2.
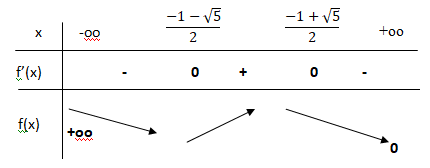
3. Expliquer pourquoi la fonction f est positive sur l’intervalle [0;+∞[.
f(0) = 2 >0.
Sur l’intervalle [0;+∞[ la fonction f décroît de 2 à 0.
4. On notera Cf
la courbe représentative de la fonction f dans un repère orthogonal .
On admet que la fonction F définie pour tout nombre réel x par
F(x) =
(−x
2 −5x −7 )
e
−x
est une primitive de la fonction f .
Soit a un nombre réel positif.
Déterminer l’aire A (a), exprimée en unité d’aire, du domaine du plan délimité par
l’axe des abscisses, la courbe Cf et les droites d’équation x = 0 et x = a.
Aire = F(a) - F(0)=(−a
2 −5a −7 )
e
−a +7 unités d'aire.
|
|
|
|