Probabilités,
suite. Bac
Amérique du Nord
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1. 5 points.
Au basket-ball, il est possible de marquer des paniers rapportant un
point, deux points
ou trois points.
Les parties A et B sont indépendantes.
Partie A.
L’entraineur d’une équipe de basket décide d’étudier les
statistiques de réussite des lancers de ses joueurs. Il constate qu’à
l’entrainement, lorsque Victor tente un panier à trois
points, il le réussit avec une probabilité de 0,32.
Lors d’un entrainement, Victor effectue une série de 15 lancers à trois
points. On suppose
que ces lancers sont indépendants.
On note N la variable aléatoire qui donne le nombre de paniers marqués.
Les résultats des probabilités demandées seront, si nécessaire,
arrondis au millième.
1. On admet que la variable aléatoire N suit une loi binomiale.
Préciser ses paramètres.
n = 15 ; p =0,32.
2. Calculer la probabilité que Victor réussisse exactement 4 paniers
lors de cette série.
P(N=4)=(4 15) x0,324 x(1-0,32)15-4=15 x14 x13 x12 / (2x3x4) x0,324 x0,6811=0,206.
3. Déterminer la probabilité que Victor réussisse au plus 6 paniers
lors de cette série.
P (N < 6) =0,828.
4. Déterminer l’espérance de la variable aléatoire N.
E = n p =15 x0,32 =4,8.
En moyenne 48 paniers sont réussis sur 150 lancers.
5. On note T la variable aléatoire qui donne le nombre de points
marqués après cette
série de lancers.
a. Exprimer T en fonction de N.
Chaque lancer vaut 3 points.
T = 3 N.
b. En déduire l’espérance de la variable aléatoire T . Donner une
interprétation
de cette valeur dans le contexte de l’exercice.
D'après la linéarité de l'espérance : E(T) = 3 E(N) = 3 x4,8 = 14,4.
En moyenne sur 150 lancers, 144 points sont marqués.
c. Calculer P(12 < T < 18).
P(12 < T=3N < 18 = P(4 < N < 6)=P(N=4)+P(N=5) +P(N=6)=0,586.
Partie B.
On note X la variable aléatoire donnant le nombre de points marqués par Victor lors
d’un match.
On admet que l’espérance E(X) = 22 et la variance V (X) = 65.
Victor joue n matchs, où n est un nombre entier strictement positif.
On note X1,X2,...,Xn les variables aléatoires donnant le nombre de points marqués au
cours des 1er, 2e
, ...,n-ième matchs. On admet que les variables aléatoires X1, X2, ..., Xn
sont indépendantes et suivent la même loi que celle de X.
On pose Mn =(
X1 + X2 +...+ Xn)/
n
.
1. Dans cette question, on prend n = 50.
a. Que représente la variable aléatoire M50 ?
M50 est la moyenne des points marqués sur 50 matchs.
b. Déterminer l’espérance et la variance de M50.
Xi suit la même loi que X. Donc E(M50) = E(X) = 22.
X1, X2, ... X50 sont indépendantes. Donc V(M50) = V(X) / 50 = 65 / 50 =1,3.
c. Démontrer que P (|M50 −22| > 3<
13 /
90
.
D'après l'inégalité de Bie,aymé-Tchébychev , pour une variable
aléatoire X d'espérance E(X), de variance V(X), pour tout réel a
>0 : P(|X-E(X)| ) > a < V(M50) / a2.
P(M50-E(M50)| ) > 3 < V(M50) / 32.
V(M50) / 32 =1,3 / 9=13 / 90.
P (|M50 −22| > 3<
13 /
90
.
d. En déduire que la probabilité de l’évènement « 19 < M50 < 25 » est strictement
supérieure à 0,85.
19 < M50 < 25 » revient à : (|M50 −22| < 3.
P( (|M50 −22| < 3)=1-P( (|M50 −22| > 3)=1-13 / 90=77 / 90 ~0,856 > 0,85.
2. Indiquer, en justifiant, si l’affirmation suivante est vraie ou fausse :
« Il n’existe aucun entier naturel n tel que
P (
|Mn −22| > 3 )
< 0,01 ».
D'après la loi faible des grands nombres, quelque soit t réel strictement pôsitif, la limite en plus l'infini de P(|Mn-E(X)| > t =0.
La limite en plus l'infini de P(|Mn-22| > 3 =0.
Il existe un rang N tel que pour tout n > N, P(|Mn-22| > 3 < 0,01.
L'affirmation est fausse.
|
...
|
....
|
Exercice 2 5 points.
Un des objectifs de cet exercice est de déterminer une approximation du nombre réel
ln(2), en utilisant une des méthodes du mathématicien anglais Henry Briggs au XVIe
siècle.
On désigne par (un) la suite définie par :
u0 = 2 et, pour tout entier naturel n, un+1 = un½.
Partie A
1. a. Donner la valeur exacte de u1 et de u2.
u1 = 2½.
u2 = u1½ = (2½)½ = 20,25.
b. Émettre une conjecture, à l’aide de la calculatrice, sur le sens de variation et
la limite éventuelle de la suite.
La suite est décroissante et converge vers 1.
2. a. Montrer par récurrence que pour tout entier naturel n, 1 < un+1 < un.
Initialisation : 1 < 2½ < 2 soit 1 < u1 < u0 est vraie.
Hérédité : 1 < un+1 < un est supposé vrai.
1 < un+1 < un soit 1½ < un+1½ < un 1½ , la fonction racine carrée étant croissante sur R+.
Donc 1 < un+2 < un+1 .
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
b. En déduire que la suite (un) est convergente.
La suite (un) est minorée par 1.
De plus un < un+1, donc la suite est décroissante.
Toute suite décroissante et minorée converge.
c. Résoudre dans l’intervalle [0 ; +∞[ l’équation x½ = x.
Pour x >0 l'équation s'écrit : x2 = x.
x2-x=0 ; x(x-1) =0.
x = 0 ou x = 1.
d. Déterminer, en justifiant, la limite l de la suite (un).
un+1 = f(un) avec f la fonction racine carrée, fonction continue sur [0 ; +oo[..
D'après le théorème du point fixe, l est solution de l'équation f(x) = x.
Les solutions sont 0 et 1. Or l > 1 donc l = 1.
Partie B.
On désigne par (vn) la suite définie pour tout entier naturel n par vn = ln(un).
1. a. Démontrer que la suite (vn) est géométrique de raison 0,5.
vn+1 = ln(un+1)= ln(un½)= ½ ln(un) = ½vn.
La suite est géométrique de premier terme v0 =ln(2) et la raison vaut q = 0,5.
b. Exprimer vn en fonction de n, pour tout entier naturel n.
vn = v0 x0,5n = ln(2) x0,5n= ln(2) / 2n.
c. En déduire que, pour tout entier naturel n, ln(2) = 2
n
ln(un).
vn = ln(un) = ln(2) / 2n.
ln(2) = 2
n
ln(un).
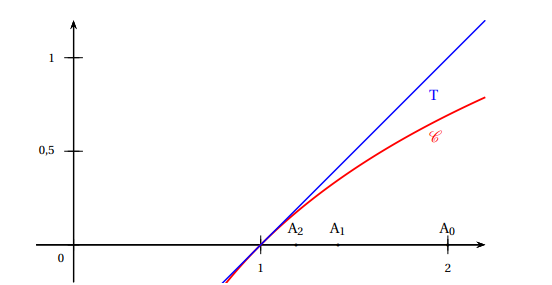
2. On a tracé ci-dessous dans un repère orthonormé la courbe C de la fonction ln et
la tangente T à la courbe C au point d’abscisse 1.
Une équation de la droite T est y = x −1.
Les points A0, A1, A2 ont pour abscisses respectives u0, u1 et u2 et pour ordonnée 0.
On décide de prendre x −1 comme approximation de ln(x) lorsque x appartient à
l’intervalle ]0,99 ; 1,01[.
a. Déterminer à l’aide de la calculatrice le plus petit entier naturel k tel que uk
appartienne à l’intervalle ]0,99 ; 1,01[ et donner une valeur approchée de uk
à 10−5 près.
Pour k < 7, uk > 1,01 et u7 ~1,00543. Donc k = 7.
b. En déduire une approximation de ln(uk).
On prend x-1 comme approximation de ln(x) lorsque x appartient à l'intervalle ]0,99 ; 1,01[.
c. Déduire des questions 1. c. et 2. b. de la partie B une approximation de ln(2).
ln(2) ~27 ln(u7)=27 x0,00543 ~0,695.
3. On généralise la méthode précédente à tout réel a strictement supérieur à 1.
Recopier et compléter l’algorithme ci-dessous afin que l’appel Briggs(a) renvoie
une approximation de ln(a).
On rappelle que l’instruction en langage Python sqrt(a) correspond à a½.
from math import*
def Briggs(a):
n = 0
while a >= 1.01:
a = sqrt(a)
n = n+1
L =2**n *(a-1)
return L
|
|
|
|