Géométrie,
fonction. Bac
Amérique du Nord
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
3. QCM. 5 points.
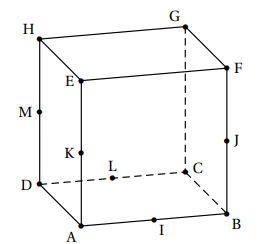
ABCDEFGH est un cube d’arête de longueur 1.
Les points I, J, K, L et M sont les milieux respectifs
des arêtes [AB], [BF], [AE], [CD] et [DH].
Affirmation 1. 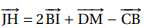 Vrai. Vrai.
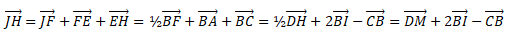
Affirmation 2. Le
triplet 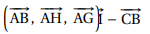 est une base de l'espace. Faux. est une base de l'espace. Faux.
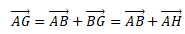
Le vecteur AG est une combinaison linéaire des deux autres vecteurs.
Les trois vecteurs étant coplanaires, ils ne constituent pas une base
de l'espace.
Affirmation 3 : 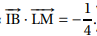 Vrai. Vrai.
A est le projeté orthogonal sur la droite (AB).
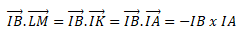
Car ces deux vecteurs sont colinéaires et de sens contraire.
-IB x IA = -0,5 x0,5 = -0,25 car l'arète du cube est de longueur 1 et I
est le milieu de (AB]
Partie B.
Dans l’espace muni d’un repère orthonormé, on considère :
- le plan P d’équation cartésienne 2x − y +3z +6 = 0
- les points A(2 ; 0 ; −1) et B(5 ; −3 ; 7)
Affirmation 4 : le
plan P et la droite (AB) sont parallèles. Faux.
Coordonnées du vecteur AB :
5-2 ; -3-0 ; 7-(-1) soit 3 ; -3 ; 8.
Coordonnées d'un vecteur n
normal au plan (P) : 2 ; -1 ; 3.
Produit scalaire de ces deux vecteurs :
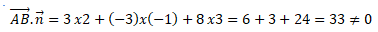
Le vecteur normal au plan (P) et le vecteur directeur de la droite (AB)
n'étant pas orthogonaux, le plan P et la droite (AB) ne sont pas
parallèles.
Affirmation 5 : Le
plan P ′ parallèle à P passant par B a pour équation cartésienne
−2x + y −3z +34 = 0. Vrai.
Les plan P et P' étant parallèles, coordonnées d'un vecteur normal au plan P' : 2 ; -1 ; 3.
Equation cartésienne du plan P' : 2x-y+3z+d = 0.
B appartient au plan P' : 2xB-yB+3zB+d = 0.
2 x5 +3+3x7+d=0 ; d = -34.
2x-y+3z+34 = 0.
Multiplier par -1 : −2x + y −3z +34 = 0.
Affirmation 6.
La distance du point A au plan P est égale à 0,5 x14½
. Vrai.
Soit H projeté orthogonal de A sur le pla P.
AH est la distance du point A au plan P.
H est l'intersection de la droite D orthogonal au plan P et passant par A(2 ; 0 ; -1).
Le vecteur n de coordonnées (2 ; -1 ; 3) est un vecteur orthogonal au plan P ; c'est donc un vecteur directeur de la droite D.
Représentation paramétrique de la droite D :
x =2t+xA = 2t+2 ; y = -t+yA = -t ; z = 3t+zA = 3t -1 avec t réel.
Intersection de la droite D et du plan P :
2(2t+2) -(-t)+3(-1+3t)+6=0.
14 t +7=0 ; t = -0,5.
Coordonnées du point H :
( 2x(-0,5 +2=1 ; 0,5 ; 3 x(-0,5)-1=-2,5).
AH2 =(1-2)2 +(0,5-0) 2 + (-2,5 +1)2 =1+0,25+2,25=3,5 = 14/4 ; AH =0,5 x14½.
On note (d) la droite de représentation paramétrique :
x = −12+2k
; y = 6
; z = 3− 5k avec k réel.
Affirmation 7. Les
droites (AB) et (d) ne sont pas coplanaires. Faux.
Coordonnées d'un vecteur directeur de la droite (d) :2 ; 0 ; -5.
Coordonnées du vecteur AB : 3 ; -3 ; 8.
Ces deux vecteurs n'étant pas colinéaires, les droites (d) et (AB) ne sont ni parallèles, ni confondues.
Représentation paramétrique de la droite (AB) :
x = 3t+xA = 3t+2 ; y = yA-3t=-3t ; z =8t+zA = 8t-1 avec t réel.
Les droites (d) et (AB) seront coplanaires si et seulement si ces deux
droites sont sécantes. Le système suivant doit avoir une solution :
3t+2 = -12+2k ; -3t = 6 ; 3-5k= 8t-1.
soit 3t=2k-14 ; t = -2 ; 8t+5k=4.
-6=2k+14 ; k = 10 ; -2*8+5*10=4 est vraie.
Le système admet une solution t = -2 et k = 10 ; les droites ont donc un point commun de coordonnées (-4 ; 6 ; -17).
Ces deux droites étant sécantes, elles sont coplanaires.
|
...
|
....
|
Exercice 4. 5 points.
On désigne par f la fonction définie sur l’intervalle [0 ; p] par
f (x) = e
x
sin(x).
On note Cf
la courbe représentative de f dans un repère.
PARTIE A
1. a. Démontrer que
pour tout réel x de l’intervalle [0 ; p],
f
′
(x) = e
x
[sin(x)+cos(x)].
On pose u = ex et v = sin(x) ; u' = ex ; v' = cos(x).
u'v+v'u = e
x
[sin(x)+cos(x)].
b. Justifier que
la fonction f est strictement croissante sur l’intervalle [
0 ; p/2].
ex est positif ; sin(x)+cos(x) >0 sur [
0 ; p/2].
f '(x) étant strictement positif sur cet intervalle, f(x) est strictement croissante sur l’intervalle [
0 ; p/2].
2 a. Déterminer une
équation de la tangente T à la courbe Cf au point d’abscisse 0.
Equation réduite de la tangente à la courbe Cf au point d'abscisse x = 0 :
y = f '(0) (x-0)+f(0) = x.
b. Démontrer que la
fonction f est convexe sur l’intervalle [
0 ; p/2].
Calcul de la dérivée seconde en posant u = ex et v = cos(x) +sin(x).
u' = ex ; v' = cos(x) -sin(x).
u'v+v'u = ex(cos(x) +sin(x)+cos(x) -sin(x))=2excos(x).
Sur l’intervalle [
0 ; p/2], la dérivée seconde est positive ; donc la fonction est convexe sur cet intervalle.
c. En déduire
que pour tout réel x de l’intervalle [
0 ; p/2].
, ex
sin(x) > x.
La courbe représentative d'une fonction convexe est située au dessus de ces tangentes.
Equation de la tangente à cette courbe en x=0 : y = x.
Sur l’intervalle [
0 ; p/2].
, ex
sin(x) > x.
3. Justifier que
le point d’abscisse p/
2
de la courbe représentative de la fonction f est
un point d’inflexion.
f ''(x) = 2excos(x).
f ''(x) a le signe de cos(x).
f ''(x) s'annule pour x = p/2 et change de signe.
La courbe présente un point d'inflexion au point d'abscisse x = p/2.
Partie B.
On note : 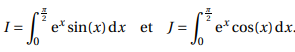
1. En intégrant par
parties l’intégrale I de deux manières différentes, établir les deux
relations suivantes :
I = 1+ J et I = ep/2 − J.
On pose u=ex et v ' = sin(x) ; u' = ex ; v = -cos(x).

On pose u=ex et v ' = cos(x) ; u' = ex ; v = sin(x).
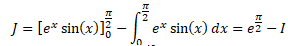
2. En déduire que I
=
(1+exp( p/2) ) /
2
.
I = 1+ J et I = ep/2 − J.
Ajouter : 2I = 1+ep/2 ; I = (1+ep/2) / 2.
3. On note g la
fonction définie sur R par g(x) = x.
Les courbes représentatives des fonctions f et g sont tracées dans le
repère orthogonal ci-dessous sur l’intervalle [0 ; p].
Calculer la valeur exacte de l’aire du domaine hachuré situé entre les
courbes Cf
et Cg et les droites d’équation x = 0 et x = p/
2
.
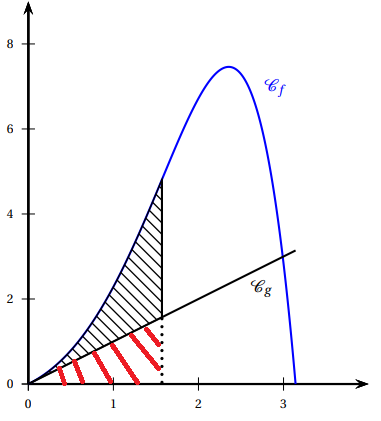
Aire comprise entre la courbe Cf et l'axe des abscisses entre x =0 et x = 0,5 p : I = (1+ep/2) / 2.
Aire du triangle rectangle hachuré en rouge : ½ * p/2 * p / 2 =p2/8.
Aire hachurée en noire : I-p2/8 = (1+ep/2) / 2 -p2/8 ~1,67 unités d'aire.
|
|
|
|