Géométrie,
fonction. Bac
Amérique du Nord
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. . 5 points.
On considère la fonction f définie sur R par
f (x) = xe
−x +2x −1.
On admet que la fonction f est deux fois dérivable sur R.
On appelle Cf sa courbe représentative dans un repère orthogonal du plan.
On note f
′
la fonction dérivée de la fonction f et f
′′ la fonction dérivée seconde de f ,
c’est-à-dire la fonction dérivée de la fonction f
′
.
Partie A : Étude de la fonction f
1. Déterminer les limites de la fonction f en −∞ et en +∞.
En plus l'infini : e-x tend vers zéro ; xe
−x tend vers zéro ; 2x+1 tend vers +oo.
Par somme des limites, f(x) tend vers +oo.
En moins l'infini : f(x) = e-x[x+(2x+1) ex].
ex tend vers zéro ; (2x+1) ex tend vers zéro ; e-x tend vers +oo.
x e-x tend vers -oo ; f(x) tend vers -oo.
2. Pour tout réel x, calculer f
′
(x).
Dérivée de x e-x en posant u = x et v = e-x ; u' = 1 ; v' = -e-x ; u'v+v'u = e-x -xe-x = e-x(1-x).
f '(x) = e-x(1-x)+2.
3. Montrer que pour tout réel x :
f
′′(x) = (x −2)e−x
.
On pose u = 1-x et v = e-x ; u'= -1 ; v' = -e-x.
u'v+v'u = e-x(-1-1+x)=(x −2)e−x
.
4. Étudier la convexité de la fonction f .
e-x > 0 ; si x > 2, f ''(x) >0 et la fonction est convexe.
si x < 2, f ''(x) < 0 et la fonction est concave.
Si x = -2, la dérivée seconde s'annule et change de signe : la courbe présente un point d'inflexion.
5. Étudier les variations de la fonction f
′
sur R, puis dresser son tableau de variations
en y faisant apparaître la valeur exacte de l’extremum.
Les limites de la fonction f
′
aux bornes de l’intervalle de définition ne sont pas
attendues.
f
′′(x) = (x −2)e−x ;
e−x > 0 ;
si x > 2, f ''(x) >0 et f '(x) est croissante.
si x <2, f ''(x) est négative et f '(x) est décroissante.
si x = 2, f ''(x) s'annule et f '(x) présente un minimum.
f '(2) = 2-e-2.

6. En déduire le signe de la fonction f
′
sur R, puis justifier que la fonction f est strictement croissante sur R.
Pour tout réel x, f '(x) > f '(2) ; f '(x) est positive.
Par conséquent, la fonction f(x) est strictement croissante sur R.
7. Justifier qu’il existe un unique réel a tel que f (a) = 0.
Donner un encadrement de a, au centième près.
La fonction f est continue car dérivable et stricterment croissante sur R.
De plus f ]-oo ; +oo[) = ]-oo ; +oo[.
D'après le théorème de la bijection, l'équation f(x) = 0 admet une solution unique sur R.
La calculatrice conduit à 0,37 < a < 0,38.
8. On considère la droite D d’équation y = 2x −1.
Étudier la position relative de la courbe Cf par rapport à la droite D.
f (x) -(2x-1)= xe
−x.
e-x est strictement positif sur R.
Le signe de
f (x) -(2x-1) est le signe de x.
Si x < 0, Cf est en dessous de la droite D.
Si x > 0, Cf est au dessus de la droite D.
Partie B : Calcul d’aire.
Soit n un entier naturel non nul. On considère l’aire du domaine Dn délimité par la
courbe Cf
, la droite D et les droites d’équations respectives x = 1 et x = n.
On note 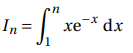
1. À l’aide d’une intégration par parties, exprimer In en fonction de n.
On pose u = x et v' = e-x ; u' = 1 ; v =- e-x.
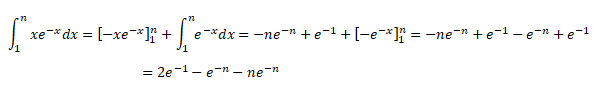
2. a. Justifier que l’aire du domaine Dn est In.
La fonction x e-x , produit de fonctions continues, est continue sur [1 ; n]
L'aire du domaine Dn est In.
b. Calculer la limite de l’aire du domaine Dn quand n tend vers +∞.
e-n tend vers zéro ; l'aire du domaine est donc 2e-1.
|
...
|
....
|
Exercice 2. QCM. 5 points.
On considère la droite D qui a pour représentation paramétrique :
x = 3− t
; y = −2+3t
; z = 1+4t
,avec t réel et le plan P qui a pour équation cartésienne : 2x −3y + z −6 = 0.
1. Affirmation : La droite D′
, qui a pour représentation paramétrique :
x = 2+2t ;
y = 4−6t
; z = 9−8t avec t réel, est parallèle à la droite D.
Vrai
Coordonnées d'un vecteur directeur de la droite D : u(-1 ; 3 ; 4).
Coordonnées d'un vecteur directeur de la droite D' : u'(2 ; -6 ; -8).
Ces deux vecteurs étant colinéaires, u'=-2u , les droites D et D' sont parallèles.
2. On admet que les points A(−2 ; 3 ; 1), B(1 ; 3 ; −4) et C(6 ; 3 ; 9) ne sont pas alignés.
Affirmation : La droite D est orthogonale au plan défini par les trois points A, B
et C. Faux.
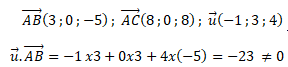
Ces deux vecteurs n'étant pas orthogonaux, la droite D n'est pas orthogonale au plan défini par les trois points A, B
et C.
3. Affirmation : La droite D est sécante avec la droite D qui a pour représentation
paramétrique :
x = −4+2t
′
; y = 1−3t
′
; z = 2+ t
′ avec t' réel. Faux.
Résolution du système :
x = 3− t et x = −4+2t
′
; 3-t = -4+2t' ; -t=-7+2t' ; t =7-2t'.
y = −2+3t
= -2+3(7-2t')=19-6t' et y = 1−3t
′.
19-6t' =1-3t' ; 18 =3 t' ; t' =6 et t=-5.
z = 1+4t =1+4*(-5)=-19 ; z =2+t'=2+6=11. Impossible.
4. Affirmation : Le point F(−3 ; −3 ; 3) est le projeté orthogonal du point E(−5 ; 0 ; 2)
sur le plan P. Vrai.
Coordonnées d'un vecteur normale au plan P : n ( 2 ; -3 ; 1).
Coordonnées du vecteur EF :( -3+5 ; -3 ; 3-2) soit (2 ; -3 ; 1).
2xF −3yF + zF −6 = -6+9+3-6=0
De plus les coordonnées de F vérifient l'équation du plan P :
.
5. Affirmation : Il existe exactement une valeur du paramètre réel a telle que le plan
P
′ d’équation −3x + y − a
2
z +3 = 0 soit parallèle à la droite D. Faux.
Coordonnées d'un vecteur normal au plan P ' : n' (-3 ; 1 ; -a2).
Coordonnées d'un vecteur directeur de la droite D : u(-1 ; 3 ; 4).
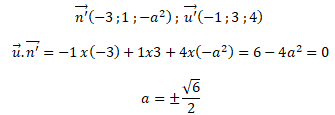
|
|
|
|