Probabilités.
Suites. Bac
Amérique du Nord
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
3. . 5 points.
Dans cet exercice, les réponses seront arrondies à 10−4
près.
Durant la saison hivernale, la circulation d’un virus a entraîné la
contamination de 2%
de la population d’un pays. Dans ce pays, 90% de la population a été
vaccinée contre ce
virus.
On constate que 62% des personnes contaminées avaient été vaccinées.
On interroge au hasard une personne, et on note les évènements suivants
:
C : « la personne a été contaminée »
V : « la personne a été vaccinée ».
1. À partir de l’énoncé,
donner, sans calcul, les probabilités P(C), P(V ) et la probabilité
conditionnelle PC (V ).
P(C) = 0,02.
P(V) = 0,90.
PC (V ) =0,62.
2. a. Calculer P(C ∩V ).
P(C ∩V ) =P(C) x P(V) = 0,02 x0,62 =0,0124.
b. En déduire P
(non C ∩V )
.
P(V) = P(C n V) +P(non C n V) .
P(non C n V) = P(V) = P(C n V)=0,9-0,0124=0,8876.
3. Recopier l’arbre
des probabilités ci-dessous et le compléter.
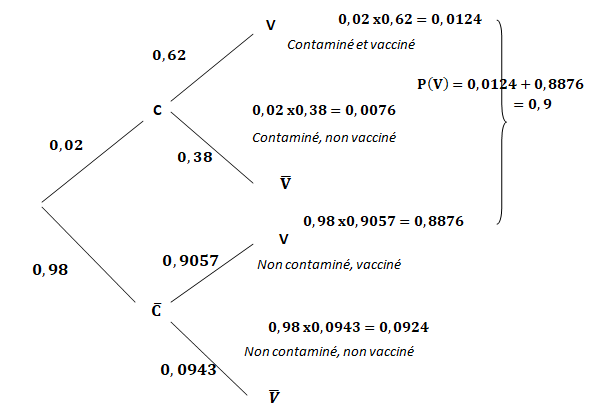
4. Calculer PV
(C) et interpréter le résultat dans le contexte de l’exercice.
PV(C) = P(V n C) / P(V) =0,124 /0,9 =0,0138.
1,38 % des personnes vaccinées ont été contaminées par le virus.
On qualifie l'événement C
5. Déterminer si
les affirmations suivantes sont vraies ou fausses en justifiant votre
réponse.
a. « Parmi les
personnes non contaminées, il y a dix fois plus de personnes vaccinées
que de personnes non vaccinées. » Faux.
Parmi les non contaminés, environ 90,57 % sont vaccinées et 9,43 % ne le sont pas ; .
90,57 / 9,43~9,6 fois plus de vaccinnés que de non vaccinés parmi les non contaminés.
b. « Plus de
98 % de la population vaccinée n’a pas été contaminée. »
Vrai.
1,38 % des vaccinés sont contaminés.
Donc 98,62 % des personnes vaccinées n'ont pas été contaminées.
6. On s’intéresse à
un échantillon de 20 personnes choisies au hasard dans la population.
La population du pays est assez importante pour qu’on puisse assimiler
ce choix à
des tirages successifs avec remise.
On note X la variable aléatoire qui à chaque tirage associe le nombre
de personnes
contaminées.
On rappelle que, pour une personne choisie au hasard, la probabilité
d’être contaminée est p = 0,02.
a. Quelle est la
loi suivie par la variable aléatoire X ? Justifier et donner ses
paramètres.
L'épreuve comporte deux issues Le succés est l'événement C de probabilité p = 0,02.
Les répétitions sont identiques et indépendantes.
X suit la loi binomiale de paramètres n = 20 et p = 0,02.
b. Calculer, en
rappelant la formule, la probabilité que 4 personnes exactement
soient contaminées dans ce groupe de 20 personnes.
P(X=4) = 204 x0,024 x0,9820-4=20 x19x18x17 /(1x2x3x4) x0,024 x0,9816=5,6 10-4 ~0,0006.
|
...
|
....
|
Exercice 4 . 5 points.
L’objectif de cet exercice est d’étudier la suite (un) définie pour tout entier naturel n par :
u0 = 0
; u1 = 0,5 ;
un+2 = un+1 −
0,25un
Partie A : Conjecture
1. Recopier et compléter le tableau ci-dessous. Aucune justification n’est demandée.
n
|
0
|
1
|
2
|
3
|
4
| 5
|
un
|
0
|
0,5
|
0,5
|
3 / 8
|
1/4
| 5 / 32
|
2. Conjecturer la limite de la suite (un).
Les termes de la suite semblent décroître tout en restant positifs.
La suite semble converger vers zéro.
Partie B : Étude d’une suite auxiliaire
.
Soit (wn) la suite définie pour tout entier naturel n par :
wn = un+1 − 0,5
un
1. Calculer w0.
w0=u1 − 0,5
u0
=0,5-0=0,5.
2. Démontrer que la suite (wn) est géométrique de raison 0,5
.
wn+1 = un+2 − 0,5
un+1 =un+1 −
0,25un
− 0,5
un+1 =0,5
un+1 −
0,25un =0,5(un+1 −
0,5un )=0,5 wn.
(Wn) est une suite géométrique de premier terme w0 = 0,5 et de raison q = 0,5.
3. Pour tout entier naturel n, exprimer wn en fonction de n.
wn = w0 x0,5n = 0,5n+1.
4. Montrer que pour tout entier naturel n, on a :
un+1 = 0,5n+1
+ 0,5
un.
wn = un+1 − 0,5
un=0,5n+1.
un+1 =0,5n+1+0,5
un.
5. Démontrer par récurrence que, pour tout n entier naturel, un = n *0,5n
.
Initialisation : u0 = 0 et d'autre part u0 = 0 *0,50 =0 *1=0.
La relation est vraie au rang zéro.
Hérédité : un = n *0,5n est supposé vraie.
un+1 =0,5n+1+0,5
un.
un+1 =0,5n+1+0,5n *0,5n =0,5n+1+n *0,5n+1 =(n+1)0,5n+1.
La relation est vraie au rang n+1.
Conclusion : la relation est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
Partie C : Étude de la suite (un)
1. Montrer que la suite (un) est décroissante à partir du rang n = 1.
un+1-un=un = (n+1) *0,5n+1
-un =(n+1) *0,5n+1
- n *0,5n
=0,5n+1 (n+1-2n)=0,5n+1 (1-n).
Pour n > 1 : 0,5n+1 est strictement positif ; 1-n est négatif ou nul.
un+1-un < 0.
La suite est décroissante à partir du rang 1.
2. En déduire que la suite (un) est convergente sans chercher à calculer la valeur de
la limite.
un = n *0,5n
.
La suite est donc minorée par zéro.
La suite est décroissante à partir du rang 1.
La suite converge vers une limite l >0.
3. On admet que la limite de la suite (un) est solution de l’équation : l =l− 0,25 l.
Déterminer la limite de la suite (un).
l =l− 0,25 l= 0,75 l.
0,25 l=0 ; l=0.
|
|
|
|