Mathématiques,
BTS groupe B1 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 . 10 points.
Pour
fabriquer de l’aluminium en feuille on chauffe une plaque d’aluminium à
250 °C puis
on la sort du four : c’est alors la phase de refroidissement. On étudie
l’évolution de la température de la plaque d’aluminium durant cette
phase.
On note f (t) la température de la plaque d’aluminium à l’instant t.
f (t) est exprimée en degré Celsius, et t désigne le nombre de minutes
de refroidissement.
Les deux parties peuvent être traitées de façon indépendante.
Partie A. Équation différentielle.
On sait que la fonction f est solution de l’équation différentielle :
(E) : y
′ +0,25y = 7,5,
où y est une fonction inconnue de la variable réelle t, définie et dérivable sur l’intervalle
[0 ;+∞[, et où y
′
est la dérivée de y.
1. Résoudre l’équation différentielle :
(E0) : y
′ +0,25y = 0.
y = A exp(-0,25t) avec A une constante réelle.
2. Soit c un nombre réel.
On considère la fonction constante g définie sur l’intervalle [0 ; +∞[ par :
g(t) = c.
Déterminer le réel c pour que la fonction g soit solution de l’équation différentielle
(E).
g' = 0 ; 0+0,25 c =7,5 ; c = 30.
3. En déduire l’ensemble des solutions de l’équation différentielle (E).
y = A exp(-0,25 t) +30.
4. Déterminer l’expression de la fonction f sachant qu’à l’instant t = 0 la température est
égale à 250 °C.
f(0) = A +30 =250 ; A = 220..
f(t) =220 exp(-0,25t) +30.
Partie B. Étude de fonction.
On considère la fonction f définie sur l’intervalle [0 ; +∞[ par :
f (t) = 220exp(−0,25t) +30.
On admet que f (t) représente la température (en degré Celsius) de la plaque d’aluminium
après t minutes de refroidissement.
1. Déterminer la valeur approchée à 0,1 °C de la température de la plaque après un quart
d’heure de refroidissement.
f(15) = 220 exp(-0,25 x15) +30 =35,2 °C.
2. Déterminer la limite de la fonction f en +∞.
Quelle est la conséquence pour la courbe représentative de la fonction f ?
Interpréter ce résultat dans le contexte de l’exercice.
Le terme en exponentielle tend vers zéro ; f(t) tend vers 30 ;
la température finale de la plaque est 30°C.
3. On admet que la fonction f est dérivable sur l’intervalle [0 ; +∞[ et on note f
′
sa fonction dérivée.
Déterminer f
′
(t) pour tout réel t de l’intervalle [0 ; +∞[.
En déduire les variations de la fonction f sur l’intervalle [0 ; +∞[.
Interpréter ce résultat dans le contexte de l’exercice.
f '(t) = 220 x(-0,25)exp(−0,25t)=-55 exp(-0,25t).
f '(t) étant négative, la fonction f(t) est strictement décroissante de 250 à 30.
4.
Un technicien affirme : « en cent secondes, la plaque a perdu cent
degrés ».
A-t-il raison ? Quelle est la durée nécessaire, arrondie à la seconde,
pour que la température de la plaque passe en dessous de 150 °C ?
Les réponses devront être justifiées.
100 s ~1,67 min.
f(1,67) = 220 exp(-0,25 *1,67) +30 = 175 °C.
La température diminue de 75 °C : l'affirmation est fausse.
150=220xexp(-0,25t) +30.
120 / 220 =exp(-0,25t)
ln(120 / 220) =-0,25t
t =ln(220 / 120) /0,25 ~2,4 min.
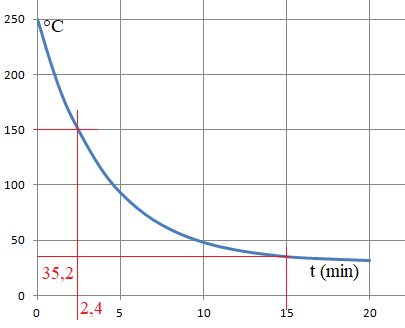
5. Réaliser sur la
copie un croquis donnant l’allure de la courbe représentative de la
fonction f . Ce croquis devra également faire apparaître les résultats
des questions 1 à 4.
|
...
|
....
|
Exercice 2 10 points.
Partie A. Loi exponentielle.
On s’intéresse au temps que doit attendre un client pour être servi à la terrasse d’un café.
On admet que ce temps d’attente, exprimé en minute, peut être modélisé par une variable
aléatoire T qui suit une loi exponentielle de paramètre l.
1. On sait que le temps d’attente moyen d’un client est égal à 4 minutes.
Expliquer pourquoi on a alors l = 0,25.
l = 1 / E(t) = 1 / 4 = 0,25.
2. Décrire par une phrase l’évènement (T < 3) et déterminer sa probabilité, arrondie à
10−3
.
Le client attend moins de 3 minutes pour être servi.
P(t < 3) = 1- exp(-0,25*3)=0,528.
3. Quelle est la probabilité qu’un client attende au moins 5 minutes ? Arrondir à 10−3
.
P(t > 5) =exp(-0,25 x5)=0,287.
4. Déterminer, à la seconde près, le temps t tel que : P(T > t) = 0,1.
exp(-0,25t) =0,1 ;
-0,25 t = ln(0,1) = -ln(10)
t = ln(10 / 0,25 ~9,21min ou 553 s.
Partie B. Probabilités conditionnelles
Un café propose des boissons chaudes et des boissons froides, qui peuvent être servies en
terrasse ou en salle.
On dispose des informations suivantes :
- 60 % des consommations sont servies en terrasse. Dans un tiers des cas, il s’agit d’une boisson chaude.
- 40 % des consommations sont servies en salle.
Parmi elles, les trois quarts sont des boissons chaudes.
On s’intéresse à une consommation choisie au hasard, et on considère les évènements suivants :
T : il s’agit d’une consommation servie en terrasse.
C : il s’agit d’une boisson chaude.
1. Dresser un arbre pondéré représentant la situation.
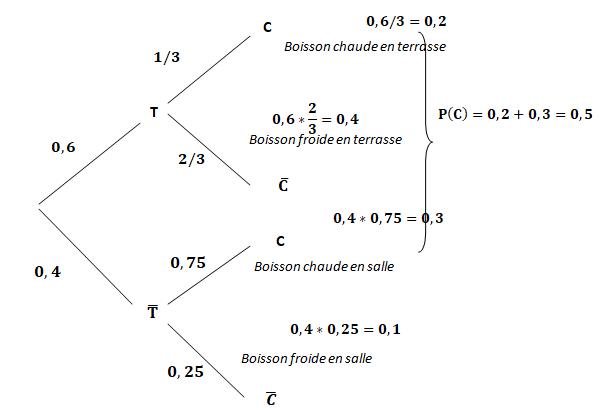
2. Déterminer la probabilité P(T ∩C).
P(T ∩C)=0,6 /3 =0,2..
3. Montrer que la probabilité que la consommation soit une boisson chaude est
égale à 0,5.
P(T ∩C) +P(non T ∩C)=0,2 +0,3 = 0,5.
.
4. Une boisson chaude vient d’être commandée. Un serveur déclare :
« Elle a davantage de chance d’être servie en salle qu’en terrasse ».
Le serveur a-t-il raison ? Justifier la réponse.
PCT =P(T ∩C) / P(C) = 0,2 / 0,5 = 0,4.
PC non T =P(nonT ∩C) / P(C) = 0,3 / 0,5 = 0,6.
Le serveur a raison.
5. Les évènements T et C sont-ils indépendants ? Justifier.
P(T) x P(C) = 0,6 x0,5 =0,3.
P(T ∩C)=0,5 diffère de 0,3.
Les évènements T et C ne sont pas indépendants.
Partie C. Intervalle de confiance
La direction d’un café souhaite estimer la proportion p d’étudiants parmi ses clients. Pour
cela, elle interroge un échantillon aléatoire de 1 000 clients. Dans cet échantillon, elle compte
525 étudiants.
1. Donner une estimation ponctuelle f de la proportion inconnue p d’étudiants.
f=525/1000 =0,525.
2. Donner une estimation de la proportion p par un intervalle de confiance avec le niveau de confiance de 90 %.
[f(1-f) /n]½ =[0,525 (1-0,525) /1000)½=0,0158.
1,65 x0,0158=0,0260.
[0,525-0,0260 ; 0,525 +0,0260] soit [0,499 ; 0,551].
3. Le patron du café affirme :
« La proportion p est obligatoirement contenue dans l’intervalle de confiance. »
A-t-il raison ? Justifier.
Non : dans 90 % des cas, p est contenue dans l'intervalle de confiance.
4. On estime que
lorsqu’un étudiant vient au café, sa consommation s’élève en moyenne
à 3,50 euros.
Chaque mois, le café reçoit 5 000 clients.
La direction du café décide d’accorder une réduction de 10 % aux
étudiants.
En supposant que la proportion p est effectivement contenue dans
l’intervalle de confiance, indiquer, sous forme d’un intervalle, le
manque à gagner mensuel pour le café.
5000 x 0,499= 2495 ; 2495 x0,35=873,25 €.
5000 x 0,551= 2755 ; 2755 x0,35=964,25 €.
|
|
=
|
|