Mathématiques,
BTS groupe B2, B3, B4, 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 . .
Pour
fabriquer de l’aluminium en feuille on chauffe une plaque d’aluminium à
250 °C puis
on la sort du four : c’est alors la phase de refroidissement. On étudie
l’évolution de la température de la plaque d’aluminium durant cette
phase.
On note f (t) la température de la plaque d’aluminium à l’instant t.
f (t) est exprimée en degré Celsius, et t désigne le nombre de minutes
de refroidissement.
Les deux parties peuvent être traitées de façon indépendante.
Partie A. Équation différentielle.
On sait que la fonction f est solution de l’équation différentielle :
(E) : y
′ +0,25y = 7,5,
où y est une fonction inconnue de la variable réelle t, définie et dérivable sur l’intervalle
[0 ;+∞[, et où y
′
est la dérivée de y.
1. Résoudre l’équation différentielle :
(E0) : y
′ +0,25y = 0.
y = A exp(-0,25t) avec A une constante réelle.
2. Soit c un nombre réel.
On considère la fonction constante g définie sur l’intervalle [0 ; +∞[ par :
g(t) = c.
Déterminer le réel c pour que la fonction g soit solution de l’équation différentielle
(E).
g' = 0 ; 0+0,25 c =7,5 ; c = 30.
3. En déduire l’ensemble des solutions de l’équation différentielle (E).
y = A exp(-0,25 t) +30.
4. Déterminer l’expression de la fonction f sachant qu’à l’instant t = 0 la température est
égale à 250 °C.
f(0) = A +30 =250 ; A = 220..
f(t) =220 exp(-0,25t) +30.
Partie B. Étude de fonction.
On considère la fonction f définie sur l’intervalle [0 ; +∞[ par :
f (t) = 220exp(−0,25t) +30.
On admet que f (t) représente la température (en degré Celsius) de la plaque d’aluminium
après t minutes de refroidissement.
1. Déterminer la valeur approchée à 0,1 °C de la température de la plaque après un quart
d’heure de refroidissement.
f(15) = 220 exp(-0,25 x15) +30 =35,2 °C.
2. Déterminer la limite de la fonction f en +∞.
Quelle est la conséquence pour la courbe représentative de la fonction f ?
Interpréter ce résultat dans le contexte de l’exercice.
Le terme en exponentielle tend vers zéro ; f(t) tend vers 30 ;
la température finale de la plaque est 30°C.
3. On admet que la fonction f est dérivable sur l’intervalle [0 ; +∞[ et on note f
′
sa fonction dérivée.
Déterminer f
′
(t) pour tout réel t de l’intervalle [0 ; +∞[.
En déduire les variations de la fonction f sur l’intervalle [0 ; +∞[.
Interpréter ce résultat dans le contexte de l’exercice.
f '(t) = 220 x(-0,25)exp(−0,25t)=-55 exp(-0,25t).
f '(t) étant négative, la fonction f(t) est strictement décroissante de 250 à 30.
4.
Un technicien affirme : « en cent secondes, la plaque a perdu cent
degrés ».
A-t-il raison ? Quelle est la durée nécessaire, arrondie à la seconde,
pour que la température de la plaque passe en dessous de 150 °C ?
Les réponses devront être justifiées.
100 s ~1,67 min.
f(1,67) = 220 exp(-0,25 *1,67) +30 = 175 °C.
La température diminue de 75 °C : l'affirmation est fausse.
150=220xexp(-0,25t) +30.
120 / 220 =exp(-0,25t)
ln(120 / 220) =-0,25t
t =ln(220 / 120) /0,25 ~2,4 min.
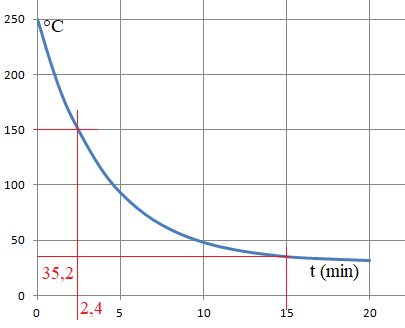
5. Réaliser sur la
copie un croquis donnant l’allure de la courbe représentative de la
fonction f . Ce croquis devra également faire apparaître les résultats
des questions 1 à 4.
|
...
|
....
|
Exercice 2
On note u(t) la tension aux bornes d’un générateur, exprimée en volt, en fonction du temps,
exprimé en seconde.
On sait que u(t) est une fonction périodique de période T = p, définie par :
u(t) = t pour t ∈ [0 ; π[.
On dit aussi que u(t) est un signal.
1. Donner la valeur de u(1), u(p), u(p+1),u(4).
u(1) = 1 ; u(p) = p ; u(p+1) = u(1) = 1;
u(4) = u(p+0,86)=u(0,86) =0,86.
2. Faire sur la copie un croquis donnant l’allure du signal u(t), sur un intervalle dont la
longueur est au moins égale à trois périodes.
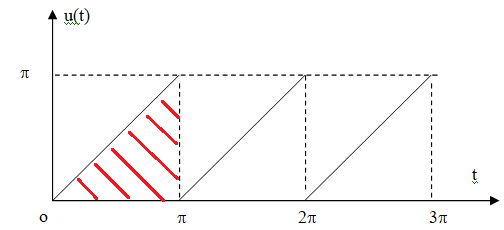
3. Un signal est dit alternatif si sa valeur moyenne sur une période est nulle.
Le signal u(t) est-il alternatif ? justifier.
Aire hachurée = p x p / 2.
Valeur moyenne = aire hachurée / période =p / 2 diffère de zéro.
u(t) n'est pas un signal alternatif.
4. Déterminer la fréquence f du signal u(t), ainsi que sa pulsation w.
fréquence f= 1 /p ; pulsation = 2 p f =2 radian /s.
5. On s’intéresse à présent au développement en série de Fourier du signal u(t).
On admet que, pour tout entier n > 1, on a :
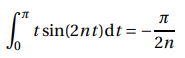
En déduire que, pour tout entier n > 1, on a :
bn = −
1
/ n
.
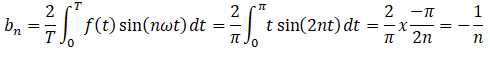
6. Les amplitudes d’un signal sont les nombres An définis par :
A0 = |a0| et, pour n > 1 An = [
(an)
2 +(bn)
2]½
.
On admet que, pour tout entier n > 1, on a an = 0.
Recopier et compléter le tableau ci-dessous.
n
|
0
|
1
|
2
|
3
|
4
|
Valeur exacte de An
|
0,5 p
|
1
|
0,5
|
1/3
|
0,25
|
Valeur approchée de An à 0,01 près
|
1,57
|
1
|
0,5
|
0,33
|
0,25
|
Le spectre d’un
signal est un diagramme en barres
dont les abscisses
sont les entiers
n > 0, et dont les
ordonnées sont les
amplitudes An.
On a représenté
ci-dessous trois
spectres.
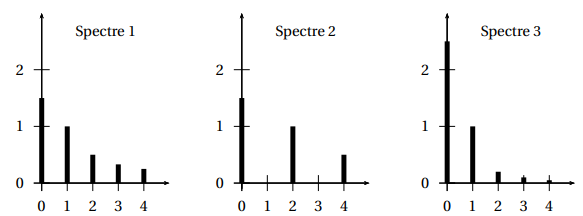
a. Expliquer pourquoi le spectre 2 ne peut pas être celui du signal u(t).
Les barres 1 et 3 sont absentes.
b. Expliquer pourquoi le spectre 3 ne peut pas être celui du signal u(t).
La barre 0 est trop grande ; les barres 2 et 3 sont trop petites.
EXERCICE 3 .
Cet exercice est constitué de deux questions indépendantes.
1. Une urne contient dix boules : sept blanches et trois noires.
Parmi les sept boules blanches, cinq portent le numéro 1 et deux portent le numéro 2.
Parmi les trois boules noires, deux portent le numéro 1 et une porte le numéro 2.
On prélève au hasard une boule dans l’urne.
a. Quelle est la probabilité que ce soit une boule portant le numéro 2 ?
2 boules blanches et une boule noire portent le n°2. Trois cas favorables sur 10 possibles.
Probabilité que la boule porte le numéro 2 : 3 /10 = 0,3.
b. On sait que la boule prélevée porte le numéro 2.
Quelle est la probabilité qu’il s’agisse d’une boule noire ?
(1 / 3) x 0,3 =0,1.
2. On considère un troupeau comportant un très grand nombre de chevaux.
On choisit au hasard un cheval et on s’intéresse à sa masse M, exprimée en kg.
On admet que la masse M est une variable aléatoire qui suit une loi normale de moyenne µ et d’écart-type s.
La densité de la variable aléatoire M est représentée ci-dessous. La zone grisée correspond à une probabilité égale à 0,95.
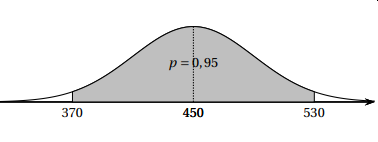
a. Indiquer sans justifier la valeur de µ.
µ = 450 kg.
b. Expliquer pourquoi s est environ égal à 40 kg
95 % des valeurs se situent à ±2 écarts types de la moyenne : (530-450) /2 = 40 kg.
|
|
|
|