Mathématiques,
BTS opticien lunetier, 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1.10 points.
Une usine produit des montures de lunettes et les vend à des opticiens.
Partie A . Statistiques.
On étudie la relation entre le prix de vente d’une monture et la recette de l’usine.
Une enquête a permis d’obtenir le résultat suivant.
x, prix de vente d'une monture
|
5
|
5,50
|
6
|
6,50
|
7
|
7,50
|
y recette de l'usine en milliers d'euros
|
17,72
|
18,21
|
18,74
|
19,12
|
19,35
|
19,85
|
Ainsi, lorsque le prix de vente d’une monture est égal à 5 euros, la recette de l’usine est égale
à 17,72 milliers d’euros, soit 17 720 euros.
1. Donner, à l’aide de la calculatrice, le coefficient de corrélation linéaire de la série (x,y).
On arrondira le résultat à 10−3.
0,994.
2. Expliquer pourquoi un ajustement affine de y en x est justifié.
Le coefficient de corrélation linéaire est proche de 1 : l'ajustement affine est justifié.
3. À l’aide de la calculatrice, donner l’équation de la droite de régression linéaire de y en
x, selon la méthode des moindres carrés, sous la forme y = ax +b.
Les coefficients a et b seront arrondis à 10−1
.
y = 0,826 x+13,67.
y = 0,8 x+13,7.
4. Selon ce modèle, quelle est la recette de l’usine, lorsque le prix de vente d’une monture
est égal à 10 euros ? Arrondir à l’euro près.
y = 0,826 x10 +13,7=21,93 ~ 22 milliers d'euros.
5. Une étude montre que, lorsque le prix de vente d’une monture est égal à 10 euros, la
recette de l’usine est, en réalité, égale à 19 950 euros.
Lorsque l’écart entre la valeur donnée par un modèle statistique et la valeur réelle est
inférieur à 5 %, on dit que le modèle est fiable.
Le modèle étudié ici est-il fiable ? Justifier.
(21,93 -19,95) / 19,95=0,099 ( environ 10 %).
Le modèle n'est pas fiable.
Partie B. Equation différentielle.
On considère l’équation différentielle :
(E) : y
′ +0,1y = 5e −0,1x
,
où y est une fonction inconnue de la variable x, définie et dérivable sur l’intervalle [0 ; +∞[,
et où y
′
est sa fonction dérivée.
1. Déterminer les solutions de l’équation différentielle
(E0) : y
′ +0,1y = 0.
y = A exp(-0,1x) avec A une constante réelle.
2. On considère la fonction g définie pour tout réel x de l’intervalle [0 ; +∞[, par :
g(x) = 5x e
−0,1x
.
On admet que la fonction g est dérivable sur l’intervalle [0 ; +∞[ et on note g
′
sa fonction dérivée.
a. Calculer g
′
(x) pour tout réel x de l’intervalle [0 ; +∞[.
On pose u = 5x et v = exp(-0,1x) ; u' = 5 ; v' = -0,1 exp(-0,1x).
u'v+v'u = 5exp(-0,1x) -0,5 x exp(-0,1x) = (5-0,5 x) exp(-0,1x).
b. En déduire que la fonction g est une solution particulière de l’équation différentielle (E).
(5-0,5 x) exp(-0,1x)+ 0,1(5x)exp(-0,1x) =5 exp(0,1x).
L'équation est bien vérifié.
3. a. En déduire que les solutions de l’équation différentielle (E) sont les fonctions h
définies pour tout réel x de l’intervalle [0;+∞[, par :
h(x) = (5A +k)e −0,1x
, où A est une constante réelle.
h(x) = A exp(-0,1x) +5x e
−0,1x =(A+5x) exp(-0,1x).
b. Déterminer, à 10 −2 près, la valeur de la constante k pour que la fonction h ci-dessus vérifie :h(5) = 17,72.
17,72 = (A+25) exp(-0,5) =0,6065(A+25)=0,6065 A +15,16 ;
A = (17,72-15,16) / 0,6065 ~4,22.
Partie C. Étude de fonction
On considère la fonction f définie pour tout réel x de l’intervalle [5 ; 15] par :
f (x) = (5x +4,22)e −0,1x
.
On a représenté ci-dessous la courbe représentative de la fonction f dans un repère
orthogonal.
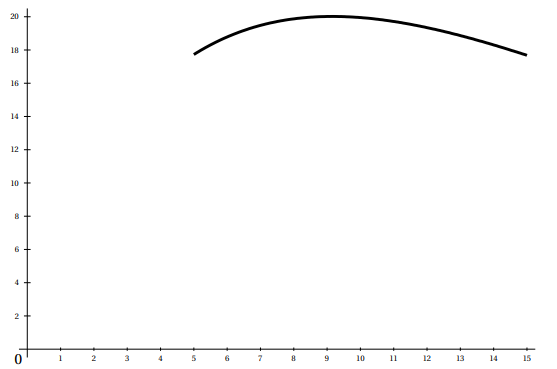 1.
1. Calculer les valeurs approchées à 10 −2 de f (5) et f (15).
f(5) = (5 x5 +4,22) exp(-0,5) ~17,72.
f(15) = (75 +4,22)exp(-1,5)~17,68.
2. On admet que la fonction f est dérivable sur l’intervalle [5 ; 15] et on note f
′
sa fonction dérivée. On admet que, pour tout réel x de l’intervalle [5 ; 15] on a :
f
′
(x) = (4,578−0,5x)e −0,1x
.
a. Déterminer le signe de f
′
(x) sur l’intervalle [5 ; 15].
e−0,1x >0.
f '(x) a le signe de 4,578 -0,5 x.
Si x < 9,156, f '(x) >0 et f(x) est strictement croissante.
Si x > 9,156, f '(x) <0 et f(x) est strictement décroissante.
b. Donner une valeur approchée à 10 −3 de f (9,156).
f (x) = (5*9,156 +4,22)e−0,9156 ~20,014.
c. En déduire le tableau de variations de la fonction f sur l’intervalle [5 ; 15].
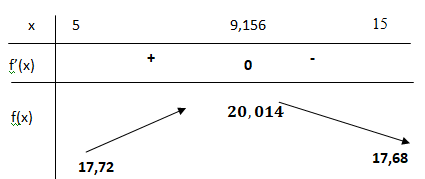 3.
3. On suppose que la fonction f modélise la recette de l’entreprise en fonction du prix de
vente d’une monture. Ainsi, lorsque le prix de vente d’une monture, en euros, est égal
à x, la recette de l’usine, en milliers d’euros, est égale à f (x).
Quel doit-être le prix de vente d’une monture pour que la recette soit maximale ?
À combien s’élève alors la recette ?
Prix de vente d'une monture : 19,16 €.
Recette : 20,014 milliers d'euros.
|
...
|
....
|
Exercice 2. 10 points.
Partie A. Probabilités conditionnelles.
Une machine contrôle des montures de lunettes. Cette machine
commet des erreurs : il arrive que des montures conformes soient
REFUSÉES, et que des montures non conformes
soient ACCEPTÉES.
On dispose des informations suivantes :
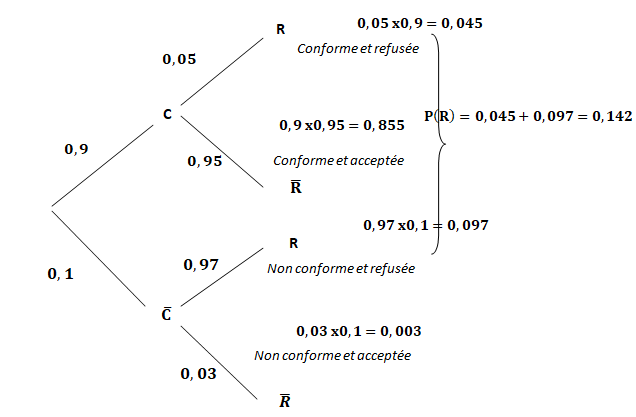
- 90 % des montures sont conformes. Parmi elles, 5 % sont REFUSÉES.
. - 10 % des montures sont non conformes. Parmi elles, 97 % sont REFUSÉES.
On prélève au hasard une monture et on considère les évènements :
-C : la monture est conforme.- R : la monture est refusée.
1. Reproduire et compléter l’arbre pondéré ci-dessous.
2. Déterminer la probabilité que la monture soit conforme et refusée.
3. Montrer que la probabilité que la monture soit refusée est égale à 0,142.
4. Un technicien affirme : « Parmi les montures refusées, plus du quart sont conformes ».
A-t-il raison ? Justifier.
PR C =P(R n C) / P(R) = 0,045 / 0,142=0,32 > 0,25. Il a raison.
5. Quelle est la probabilité que la machine commette une erreur?
P(C n R) + P(non C n non R) =0,045 +0,003=0,048.
Partie B. Loi binomiale et loi normale.
On considère un grand stock de montures de lunettes. On sait que
la proportion de montures
ayant été refusées au contrôle de conformité est égale à 0,142.
On prélève au hasard un échantillon de 1000 montures.
On considère la variable aléatoire X qui donne le nombre de montures
qui, au sein de l’échantillon de 1000 montures, ont été refusées au
contrôle de conformité.
1. On admet que la variable aléatoire X suit une loi binomiale.
Donner ses paramètres.
n =1000 ; p =0,142.
2. Déterminer la probabilité qu’au plus 12 % des montures de l’échantillon aient été refusées. Arrondir à 10−3
.
P(X < 120)~0,024.
3. On décide d’approcher la variable aléatoire X par une variable aléatoire Y suivant une
loi normale, ayant pour moyenne m = 142 et pour écart-type s = 11.
Justifier les valeurs de m et s.
m= n p = 1000 x0,142 =142.
s =[n p (1-p)]½ =[1000 * 0,142 x 0,858]½ ~ 11.
4. On a représenté ci-dessous la densité de la loi normale de moyenne m = 142 et d’écarttype s = 11.
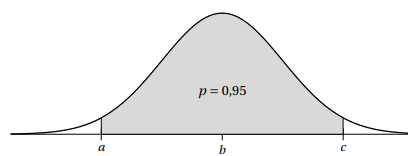
Donner une valeur approchée du réel b puis des réels a et c.
Par symétrie b = m = 142.
L'intervalle [a ; c] est l'intervalle de ± écart type.
a = 142 -2 *11 =120 ; c =142 +2 *11=164.
Partie C. Test d’hypothèse.
Une usine possède un grand stock de vis destinées à l’assemblage des montures. La longueur
des vis doit être égale à 3 mm. Afin de contrôler cette longueur, on prélève un échantillon
aléatoire de 400 vis et on réalise un test bilatéral au seuil de signification de 5 %.
Notations : L désigne la variable aléatoire qui donne la longueur (en millimètres) d’une vis prise
au hasard dans le stock. Cette variable aléatoire suit une loi normale de moyenne inconnue µ et d’écart-type 0,1.
L désigne la variable aléatoire qui donne la moyenne des longueurs (en millimètres)
des vis d’un échantillon aléatoire de 400 vis.
Hypothèses : L’hypothèse nulle est H0 :µ = 3. L’hypothèse alternative est H1 : µ diffère de 3.
1. On se place sous l’hypothèse nulle. On admet que, sous cette hypothèse, la variable
aléatoire L suit une loi normale de moyenne 3 et d’écart-type 0,1/
400½
.
Déterminer le réel positif h vérifiant P(3−h < non L < 3+h) = 0,95. Arrondir à 10−2
.
h = 2 *0,1 / 400½ =0,01.
Intervalle d'acceptation de H0 : [3-0,01 ; 3+0,01] =[2,99 ; 3,01].
2. Énoncer la règle de décision du test.
Si la moyenne des longueurs est comprise entre 2,99 et 3,01 mm, l'hypothèse H0 est acceptée.
Sinon on rejette H0 avec un risque de 5 %.
3. On prélève un échantillon aléatoire de 400 vis. Les longueurs de ces vis figurent dans
le tableau ci-dessous.
Longueur (mm)
|
2,98
|
2,99
|
3,00
|
3,01
|
3,02
|
effectif
|
48
|
92
|
240
|
18
|
2
|
a. Quelle est la longueur moyenne des vis de cet échantillon ?
(18 x2,98 +92 x2,99 +240 x3 +18 x3,01 +2x3,02) / 400 = 2,99585.
b. Conclure en appliquant la règle de décision.
2,99585 appartient à l'intervalle [2,99 ; 3,01 ] : H0 est acceptée.
|
|
|
|