Mathématiques.  Concours Contrôleur des douanes 2025 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . .. . . . . .. .. ...... ... Exercice 1. (branche commerciale) L’espace est muni d’un repère orthonormé. On note D la droite passant par les points A(3 ; −3 ; 0) et B(4 ; −1 ; −1). 1. Démontrer qu’une représentation paramétrique de la droite D sachant que t appartient à R , est : x = 3+ t y = −3+2t z = −t. Coordonnées du vecteur AB, vecteur directeur de la droite D. 4-3 ; -1+3 ; -1-0 soit : 1 ; 2 ; -1. Représentation paramétrique de la droite D : x =t+xA = t+3. y = 2t+yA = 2t-3. z = -t+zA = -t. 2. On note D′ la droite ayant pour représentation paramétrique, sachant que k est réel : x = 3k +1 y = −k +3 z = k −2 a. Donner un vecteur directeur de la droite D′. 3 ; -1 ; 1. b. Démontrer que les droites D′ et D sont orthogonales. 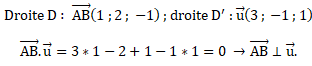c. Démontrer que les droites D′ et D ne sont pas sécantes. Dans l'hypothèse ou ces droites sont sécantes : t+3 = 3k+1 ; t = 3k-2. 2t-3 = -k+3 ; 6k-4-3=-k+3 ; 7k=10 ; k = 10 / 7. Par suite t = 30 / 7-2 = 16 /7. -t =k-2 ; t = 2-k= 2-10 / 7 = 4 / 7, ce qui est imposible. L'hypothèse étant fausse, les droites D et D' ne sont pas sécantes. 3. On considère le plan P d’équation 2x + y +4z −3 =0 a. Démontrer le que le plan P contient la droite D. Dans l'hypothèse ou le plan P contient la droite D : 2xA + yA +4zA −3 =0. 2*3+(-3)+4*0-3 =0 est vérifié. 2xB + yB +4zB −3 =0. 2*4-1-4*1-3=0 est vérifié. Donc le plan P contient la droite D. b. Démontrer que le plan P et la droite D′ se coupent en un point C dont vous préciserez les coordonnées. Dans l'hypothèse ou le plan P et la droite D' se coupent en C, il existe une valeur unique de k. 2xC + yC +4zC −3 =0. xC = 3k +1 yC = −k +3 zC = k −2. 2(3k+1)-k+3+4(k-2)-3 =0 9k = 6 ; k =2/3. Donc le plan P et la droite D' se coupent en C. xC = 3k +1=2+1=3. yC = −k +3=-2/3+3=7/3. zC = k −2= 2/3-2=-4/3.. 4. On considère la droite D passant par le point C et de vecteur directeur v (1 ; 2 ; −1) a. Démontrer que les droites D et D sont strictement parallèles. Le point C appartient à la droite D par définition. De plus le point C appartient à la droite D ′ .  Les droites D et D ′ ne sont pas sécantes, le point C n’appartient donc pas à la droite D. Par suite les droites D et D ne sont pas confondues. Les droites D et D sont parallèles non confondues, donc elles sont strictement parallèles. b. Démontrer que les droites D et D′ sont sécantes. Le point C appartenait à D et à D ′ ;  le point C appartient donc à leur intersection.  D et D sont parallèles, et D et D ′ sont orthogonales, donc D et D ′ sont orthogonales. Elles ne sont pas confondues. Les droites D et D ne sont pas confondues et possèdent le point C en commun, donc elles sont sécantes en C. Exercice 1. (branche surveillance) Dans une fête foraine, un ticket enfant permet d’effectuer autant de tirs successifs qu’il est nécessaire pour crever un ballon. À chacun de ses tirs, on considère qu’un enfant a la probabilité 0,2 de crever le ballon. Le tireur s’arrête quand le ballon est crevé. 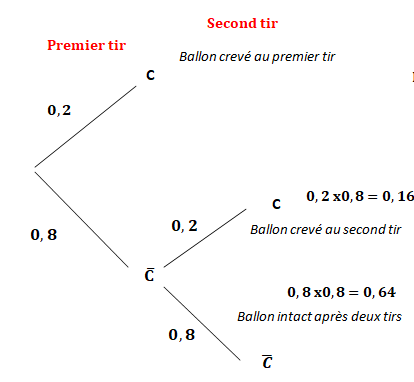1. a. Quelle est la probabilité qu’au bout de deux tirs le ballon soit intact ? On note C l'événement "le ballon est crevé". 0,8 x0,8 = 0,64. b. Quelle est la probabilité que deux tirs suffisent pour crever le ballon? C'est l'événement contraire de l'événement " le ballon est intact après  2 tirs". 1-0,64 = 0,36. c. Quelle est la probabilité p que n tirs suffisent pour crever le ballon ? La probabilité de l'événement " au bout de n tirs le ballon est intact " est : 0,8n. La probabilité de l'événement contraire " au bout de n tirs le ballon est crevé" est p = 1-0,8n. 2. Un deuxième stand de tir propose la règle suivante : - le joueur lance un dé tétraédrique régulier dont les faces sont numérotées de 1 à 4 (la face obtenue avec un tel dé est la face cachée). - Soit k le numéro de la face obtenue, le joueur peut réaliser au maximum k tirs pour crever le ballon. Déterminer la probabilité de crever le ballon. Pour indications 0,83 = 0,512 et 0,84 ≈ 0,41. On appelle D la variable aléatoire donnant le résultat du lancer du dé. Le dé étant régulier, on aura : P(D = 1) = P(D = 2) = P(D = 3) = P(D = 4 ; il y a quatre résultats possibles, chaque de ces probabilités est égale à 0,25. La probabilité que k tirs suffisent pour crever le ballon est pk = 1−0,8k. D’après la formule des probabilités totales, la probabilité de crever le ballon est : P(D = 1)× p1 +P(D = 2)× p2 +P(D = 3)× p3 +P(D = 4)× p4 = 0,25( p1 + p2 + p3 + p4 ) =0,25( 0,2+0,36+( 1−0,83) + ( 1−0,84)) ~ 0,25(0,2+0,36+1−0,512+1−0,41) ~0,25 ×1,638 ≈ 0,41. Exercice 2.(branche commerciale). Soit f la fonction définie sur l’intervalle ]0 ; +∞[ par f (x) = x −ln(x) / x2 . On appelle C sa courbe représentative dans un repère orthonormé 1. Soit u la fonction sur l’intervalle ]0 ; +∞[ par : u(x) = x3 −1+2ln(x). a. Étudier le sens de variation de la fonction u sur l’intervalle ]0 ; +∞[. u'(x) = 3x2+2/x >0. u(x) est strictement croissante sur ]0 ; +oo[. b. Calculer u(1) et en déduire le signe de u(x) pour x appartenant à ]0 ; +∞[. u(1)=1-1+2ln(1) =0. u(x) >0 sur ]1 ; +oo[ ; u(x) < 0 sur ]0 ; 1[. 2. a. Déterminer la limite de f en 0 et en +∞. En zéro : -ln(x) / x2 tend vers plus l'infini ; f(x) tend vers +oo. En plus l'infini : par croissance comparée ln(x) / x2 tend vers zéro et f(x) tend vers +oo. On remarquera que : ln(x)/x2=1 /x *ln(x) / x pour tout x appartenant à l’intervalle ]0 ; +∞[. Interpréter graphiquement la limite de f en 0. L'axe des ordonnées est asymptote verticale à la courbe C. b. Déterminer la fonction f ′, dérivée de f et construire le tableau de variation de la fonction f . Dérivée de ln(x) / x2. On pose u = ln(x) et v = x2 ; u' = 1 /x ; v' = 2x. (u'v-v'u) / v2 = (x-2xln(x)) / x4 =(1-2ln(x) / x3. f '(x) = 1-(1-2ln(x) / x3= (x3-1+2ln(x) ) / x3= u(x) / x3. u(x) >0 sur ]1 ; +oo[ ; u(x) < 0 sur ]0 ; 1[. x3 >0 sur ]0 ; +oo[. 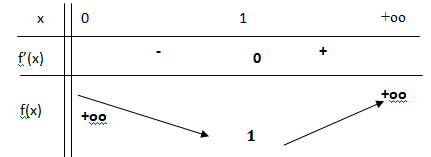3. a. Déterminer la position de C par rapport à la droite D d’équation y = x. f (x) - x =−ln(x) / x2 . Si x appartient à ]0 ; 1[ : f(x)-x  >0. C est au dessus de la droite D. Si x appartient à ]1 ; +oo[ : f(x)-x  < 0. C est en dessous de la droite D. b. Calculer lim[ f (x)−x] lorsque x tend vers +∞. Interpréter graphiquement ce résultat. f (x) - x =−ln(x) / x2 . En +oo, f(x)-x tend vers zéro. La droite D est asymptote oblique à la courbe C. Exercice 2. ( branche surveillance). On considère la fonction f définie sur l’intervalle [0; 1] par : f (x) =2x e−x . On admet que la fonction f est dérivable sur l’intervalle [0; 1]. Pour l’exercice on considérera que ln(2) ~ 0,69, e−0,1 ~0,90 et e−1 ~ 0,37. 1. a. Résoudre sur l’intervalle [0; 1] l’équation f (x) = x. x = 2xe-x ; 1 = 2e-x ; 0,5 = e-x ;ln(0,5) = -x ; x = ln(2)~0,69. b. Démontrer que, pour tout x appartenant à l’intervalle [0 ; 1], f ′(x) = 2(1−x) e−x . On pose u = 2x et v = e-x. u' = 2 ; v' = -e-x. u'v+v'u = 2e-x-2xe-x = 2(1-x)e-x. c. Donner le tableau de variations de la fonction f sur l’intervalle [0; 1]. e-x étant positif, le signe de la dérivée est celui de 1-x. Sur l’intervalle [0; 1], f(x) est positive et f(x) est croissante. 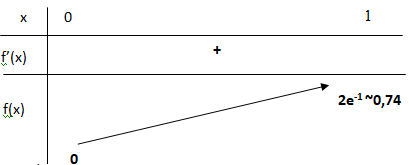On considère la suite (un) définie par :  u0 = 0,1 un+1 = f (un) pour tout entier naturel n. 2. a. Démontrer par récurrence que, pour tout n entier naturel, 0<un < un+1 <1. Initial : u1 = f(u0) = f(0,1) =0,2e-0,1 ~0,2 *0,9 ~0,18. La propriété est vraie au rang 0. Hérédité : 0<un < un+1 <1 est supposé vrai. La fonction f étant strictement croissante sur [0 ; 1] : f(0)<f(un) < f(un+1 )< f(1). 0 < un+1 < un+2 < 0,74. 0 < un+1 < un+2 < 1. La propriété est vraie au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout entier naturel n. b. En déduire que la suite (un) est convergente. un < un+1, la suite est croissante et la suite est bornée par 1, donc elle converge. c. Démontrer que la limite de la suite (un) est l= ln(2). Pour n suffisamment grand : un = un+1 ; l = f(l) =2 l exp(-l) ; la solution l = 0 n'est pas retenue car u0 = 0,1.. 0,5 = exp(-l) ; ln(0,5) = -ln(2) = -l ; l = ln(2). ... =  = .... EXERCICE 3. ( Branche commerciale).  Amateur de mots croisés, Mathias s’entraîne sur un site internet. 40% des grilles qui y sont proposées sont de niveau facile, 30% sont de niveau moyen et 30% de niveau difficile. Mathias sait qu’il réussit les grilles de niveau facile dans 95% des cas, de niveau moyen dans 60% des cas et de niveau difficile dans 40% des cas. Une grille de mots croisés lui est proposée de façon aléatoire. On considère les évènements suivants : F : « La grille de mots croisés est de niveau facile. »; M : « La grille de mots croisés est de niveau moyen. »; D : « La grille de mots croisés est de niveau difficile. »; R : «Mathias réussit la grille. » et non R son évènement contraire. 1. Traduire les données de l’énoncé à l’aide d’un arbre pondéré. 2. a. Calculer la probabilité que la grille de mots croisés proposée soit de niveau difficile et que Mathias la réussisse. 0,3 x0,4 = 0,12. b. Calculer la probabilité que la grille de mots croisés proposée soit de niveau facile et que Mathias ne la réussisse pas. 0,4 x0,05 = 0,02. c. Montrer que la probabilité que Mathias réussisse la grille proposée est égale 0,68. 3. Sachant que Mathias n’a pas réussi la grille proposée, quelle est la probabilité que ce soit une grille de mots croisés de niveau moyen ? 0,12 / (0,02+0,12+0,18)=0,375. 4. Mathias a réussi la grille proposée. Sa petite soeur Elyne affirme : « Je pense que ta grille était facile ». Dans quelle mesure a-t-elle raison? Justifier la réponse à l’aide d’un calcul. 0,38 / 0,68 ~0,56 > 0,5. Elyne a plus d'une chance sur deux d'avoir raison. Exercice 3. (branche surveillance) L’espace est rapporté à un repère orthonormé.  On considère le plan P caractérisé par le point A(4 ; 2 ; −1) et les vecteurs u( (3 ; 1 ; 5) et v(−2 ; −1 ; 0). 1. Vérifier que ces vecteurs ne sont pas colinéaires. Donc ces vecteurs ne sont pas colinéaires. 2. Les points P(5; 2; 4) et Q(0 ; −1 ; 10) appartiennent-ils au plan P ? 1 = 3a +2b ; 0 = a-b soit a = b.. Par suite 1=3a-2a =a ; a=b= 1. 5=5a+0b est bien vérifiée; donc P appartient au plan (P) 3. Le point S(7 ; −2 ; 10 / 3) appartient-il à la droite (PR) où R(2; 3; 3) ? Ces deux vecteurs n'étant pas colinéaires, le point S n'appartient pas à la droite (PR). 4. Calculer les distances PQ et PR. PQ2 =(0-5)2 +(-1-2)2 +(10-4)2 =25+9+36=70 ; PQ = 70½. PR2 =(2-5)2 +(3-2)2 +(3-4)2 =9+1+1=11 ; PR = 11½. Exercice 4. (branche commerciale). Le nombre d’arbres de la forêt de Xivry, en milliers d’unités, est modélisé par la suite (un) où un désigne le nombre d’arbres, en milliers, au cours de l’année (2024+n). En 2024, la forêt de Xivry possède 50 000 arbres. Afin d’entretenir cette forêt vieillissante, l’ONF, l’Office National des Forêts, décide d’abattre chaque année 5% des arbres existants et de replanter 3 000 arbres. Pour cette exercice, on donne les données suivantes : 0,955 ≈ 0,7737; 0,956 ≈ 0,7350; 0,957 ≈0,6983 0,944 ≈ 0,7807; 0,945 ≈ 0,7339; ln(0,4) /ln(0,95) ≈ 17,86; ln(0,6) /ln(0,95)≈ 9,95; ln(0,5)/ ln(0,95)≈ 13,51,95; ln(0,5) /ln(0,94)≈ 8,25; ln(0,5) /ln(0,95)≈12,51; N. B : toutes ces données ne sont pas nécessairement utilisables. 1. Montrer que la situation peut être modélisée par :  u0 = 50 un+1 = 0,95un +3 pour tout entier naturel n. 50 milliers d'arbres en 2024 : u0 = 50. 5 % des arbres sont coupés chaque année ; il en reste 0,95 un. On en plante 3 milliers chaque année :un+1= 0,95 un +3. 2. On considère la suite (vn) définie pour tout entier naturel n par la relation : vn = 60−un. a. Montrer que la suite (vn) est une suite géométrique de raison 0,95. vn+1 = 60-(0,95 un +3)= 57-0,95 un=0,95 (60-un) = 0,95 vn. b. Calculer v0. Déterminer l’expression de vn en fonction de n. v0 =60-u0=60-50 =10. vn = v0 x0,95n =10 x0,95n. c. Démontrer que pour tout entier naturel n, un = 60−10×(0,95)n . un = 60−vn = 60-10 x0,95n. 3. Déterminer le nombre d’arbres de la forêt en 2029. On donnera une valeur approchée arrondie à l’unité. n=5 ;  u5 = 60-10 x0,955~52 milliers. a. Vérifier que pour tout entier naturel n on a l’égalité un+1 −un = 0,5×(0,95)n . un =  60-10 x0,95n. un+1 =  60-10 x0,95n+1. un+1 −un = 10 x0,95n -10 x0,95n+1=.10 x0,95n(1-0,95)=0,5 x0,95n. b. En déduire la monotonie de la suite. un+1 −un > 0 ; la suite est croissante. 4. Déterminer l’année à partir de laquelle le nombre d’arbres de la forêt aura la dépassé de 10% celui de 2024. un > 55 ;  60-10 x0,95n > 55. 5-10 x0,95n > 0 ; 10 x0,95n < 5 ; 0,95n < 0,5. n ln(0,95) < ln (0,5) ; n > ln(0,5) / ln(0,95) ; n > 12,5 ; n > 13 ; n =14 année 2038. 5. Déterminer la limite de la suite (un). Interpréter. -1 < 0,95 < 1. Si n tend vers l'infini, 0,95n tend vers zéro : un =  60-10 x0,95n tend vers 60 milliers d'arbres. Au bout d'un  temps suffisamment long, la forêt comptera 60 milliers d'arbres. Exercice4. Branche surveillance. Soit f la fonction définie sur ]0 ; +∞[ par 1. Que vaut f (1) ? 2. Étudier le signe de f sur ]1 ; +∞[, puis sur ]0; 1[. Sur les deux intervalles f(x) est positive. 3. Calculer f ′(x) pour tout x > 0. f '(x) = ln(x) -ln(1) = ln(x). 4. Dresser le tableau de variations de f sur ]0 ; +oo[ (on n’étudiera pas les limites en 0 et +oo. Vérifier les réponses obtenues à la question 2. On a bien f(x) >0. 5. Une intégration par partie nous donne : Calculer f (x) pour tout x > 0. f(x) = [t ln(t)]1 x -[t]1 x =x ln(x)-x+1. 6. En déduire : a. la valeur de f ( e). f(e) = e ln(e)-e+1 = e-e+1 = 1. b. la limite de f en 0. x ln(x) tend vers zéro. x ln(x)-x tend vers zéro ; f(x) tend vers 1. c. la limite de f en +∞. x (ln(x)-1) tend vers +oo. x(ln(x)-1)+1 tend vers +oo.

menu