Tension
de surface, loi de Laplace ; capillarité, loi de Jurin. Agrégation
2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Tension
de surface, loi de Laplace.
On
apprend en général qu'un liquide adopte laforme du récipient qui le
contient. Ce n'est pas tout à fait exact pour les petits systèmes : une
petite quantité de liquide se présente souvant comme une goutte
sphérique. La surface d'un liquide est soumise à une tension
superficielle, un peu comme une membrane élastique.
1.
Le texte suivant propose une origine microscopique à cette tension
superficielle.
Un
liquide est un état condensé : les molécules s'attirent. Lorsque cette
attraction l'emporte sur l'agitation thermique, les molécules passent
d'une phase gazeuse à une phase dense mais encore désordonée : un
liquide. les molécules au sein du liquide bénéficient d'interactions
attractives avec toutes leurs voisines et sont dans un état "heureux".
Au contraire, àla surface du liquide, elles perdent la moitié de leurs
interactions cohésives et sont "malheureuses". ( tiré de Gouttes,
bulles, perles et ondes, Belin 2005).
- Le
texte ne précise pas l'état des molécules dans la phase gaz. A
l'équilibre de phase sont-elles "heureuses" ou malheureuses" ?
A
l'équilibre de phase, les molécules possèdent le même potentiel
chimique dans les deux phases dans tout le volume des phases : elles
sont donc "heureuses". Seules les molécules proches de l'interface
sont" malheureuses".
- La
cohésion d'un liquide tel qu'une huile est due à des interactions de
type Van der Waals et l'énergie de cohésion par molécule est de l'ordre
de kBT. Donner l'ordre de grandeur d'une
dimension
moléculaire et en déduire, par analyse dimensionnelle, l'ordre de
grandeur de l'énergie par unité de surface g
associée à l'existence d'une interface à températre ambiante. Comparer
à la valeur de g
pour l'eau (72,8 mJ m-2 ). Commenter.
Chaque molécule située à l'interface perd la moitié de l'énergie de
cohésion soit ½kBT. Elle occupe une surface
a2 ( a ~1 nm).
g
= ½kBT /a2
~0,5*1,38 10-23 *293 / 10-19~
2 10-3 J m-2~2 mJ m-2.
L'énergie par unité de surface
de l'eau est plus grande du fait des liaisons hydrogène.
La tension de surface g
est définie mécaniquement de la manière suivante. Considérons
l'interface entre deux fluides.
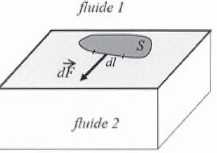
Soit
une surface S et un élément de longueur dl du contour de S.Tout se
passe comme si l'interface extérieure à S exerçait sur dl une force dF
perpendiculaire à dl, dirigée vers l'extérieur de S et de
norme dF
=gdl.
2.
Calculer le travail des
forces superficielles quand l'aire A de la surface S augmente de dA (
on pourra se limiter à une surface S rectangulaire). Conclure quant à
la cohérence de cette défiition mécanique de g et
l'approche énergétique de la question précédente.
Soit un rectangle de longueur a et de largeur b.
Norme de la force capillaire s'exerçant sur la largeur : gb.
Travail de cette force lorsque a augmente de da : W
= g
b da = g
dA.
On retrouve la définition énergétique de g :
travail qu'il faut fournir pour augmenter l'aire d'une unité.
On
considère maintenant une surface S infinitésimale cylindrique, courbée
dans une direction avec un rayon de courbure R. Sur la figure ne sont
représentées que les forces s'exerçant sur les côtés non courbés
l'angle dq
est infinitésimal, même si cela n'apparaît pas sur la figure.
3. Calculer la
projection sur l'axe Oz des forces capillaires s'exerçant sur S.
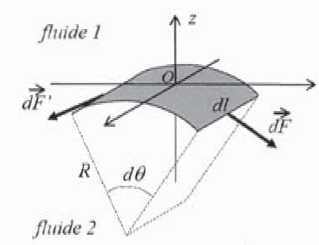
La projection des forces
s'exerçant sur les côtés courbés est nulle.
Les deux forces dF ont la même projection : dFz = -gdl
sin (½dq)~
-½gdl
dq.
|
| .
. |
|
|
4. Faire le bilan
des forces s'exerçant sur S. En déduire une relation entre g, R
et les pressions P1 et P2
des deux phases fluides.
Il
faut ajouter à la tension superficielle, les forces pressantes
s'exerçant de chaque côté de l'interface. Aire de la surface S : dl R dq.
Projection des forces sur Oz : P2dl
R dq-P1dl
R dq-gdl
dq
= 0.
P2-P1
= g / R.
5.
Justifier que pour une interface sphérique P2-P1
=2 g / R.
( équation de Laplace)
S étant une portion de sphère, les quatre forces capillaires
élémentaires ont une projection sur Oz qui n'est pas nulle. Le milieu d'indice 2 contient le centre de courbure.
6.
Quelle est la pression dans une goutte d'eau de rayon 1 mm
environnée d'air à la pression atmosphérique ? Même question
pour
une bulle d'air dans l'eau liquide environnante à la pression
atmosphérique. Pour l'interface eau-air g = 70
mN m-1.
Peau-Pair
=2 g / R = 2*70 10-3
/10-3 =140 Pa.
Bulle
d'eau dans l'air : Peau= Pair
+140 Pa, l'écart relatif de pression est négligable.
Bulle d'air dans l'eau : Pair - Peau=2
g / R = 2*70 10-3
/10-3 =140 Pa.
7. Une
bulle de savon est constituée d'une double interface liquide-air. Pour
chaque interface g~20
mN m-1. Quelle est la pression dans une bulle de
savon de rayon 1 cm ?
Pbulle -Pair = 4
g / R =4*20 10-3
/ 0,01 = 8 103 Pa.
|
|
|
|
Capillarité et gravité.
Loi de Jurin.
10. On considère un fluide de masse volumique r au repos dans un référentiel galiléen. Ce fluide se trouve dans un champ de pesanteur uniforme
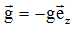 (g
>0 et l'axe Oz est suivant la verticale ascendante ). Faire le bilan
des forces s'exerçant sur un élément de volume dxdydz centré sur
un point M de coordonnées (xM, yM, zM). (g
>0 et l'axe Oz est suivant la verticale ascendante ). Faire le bilan
des forces s'exerçant sur un élément de volume dxdydz centré sur
un point M de coordonnées (xM, yM, zM).
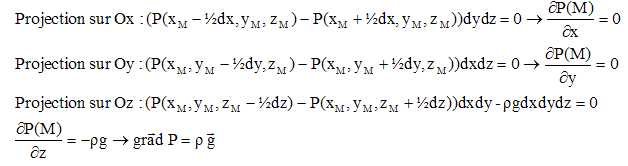
11. Démontrer alors que la surface libre d'un liquide à l'équilibre dans un récipient immobile est horizontale.
La surface libre du liquide est une équipotentielle du champ de pesanteur.
Dans le cas d'un champ de pesanteur uniforme, les équipotentielles sont perpendiculaires au champ vertical, donc horizontales.
12. En réalité près des bords du récipient, la surface libre est courbée et forme un ménisque.
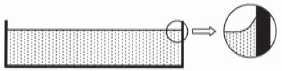
L'extension LC de ce ménisque dépend de la compétition entre la pesanteur et les forces de tension superficielle.
- Quels sont les paramètres dont dépend LC ?
- Par analyse dimensionnelle, déterminer la relation liant LC à ces paramètres. Donner ensuite l'ordre de grandeur de LC pour l'eau.
La pression dans un fluide dépend de sa masse volumique (ML-3 ) et du champ de pesanteur ( L T-2).
Les forces capillaires dépendent de la tension superficielle g ( N m-1 ou M T-2).
LC ~ ra gb gc ; [LC ]=MaL-3a Lb T -2bMc T -2c =Ma+cL-3a+b T -2b-2c= L.
Par identification LC ~ r-½ g-½ g½ ; LC eau (20°C)~ (1000*9,8)-½ *(73 10-3)½ ~0,010 *0,27 ~3 mm.
13.
Les effets de tension superficielle sont encore plus manifestes si l'on
enfonce un tube de petit rayon r dans de l'eau. Pour un tube en verre
très propre, on observe la situation schématisée ci-dessous. On note H
l'ascension capillaire dans le tube.
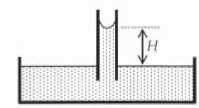
- A
quelle condition sur r la forme du ménisque dans le tube est-elle
hémisphérique ? On suppose cette condition réalisée par la suite.
L'effet de la gravité doit être négligeable. Le rayon du tube doit être petit devant LC.
- En
raisonnant sur la valeur de la pression en différents points du fluide,
démontrer la loi de Jurin, qui donne l'ascension H en fonction du rayon
r :
H = 2g / (rgr).
Pression dans l'air : Patm ;
pression dans le liquide en haut du tube ( loi de Laplace) : Ptube -Patm = -2g / r ;
pression dans le liquide au niveau de la surface libre horizontale P0 ;
relation fondamentale de l'hydrostatique : Patm-Ptube = rgH.
Loi de Jurin : rgH = 2g / r ; H = 2g / (rgr).
- Calcuer H pour l'eau si r = 100 µm.
H = 2*0,073 / (1000*9,8 *100 10-6)=0,15 m.
Pression de la sève montant dans les arbres.
La
circulation montante de la sève depuis les racines jusqu'aux feuilles
se fait dans un réseau de vaisseaux dont le diamètre varie de la
centaine à la dizaine de micromètres suivant la nature de l'arbre et la
position du vaiseau. On suppose que la sève montante n'est composée que
d'eau et que l'eau au niveau du sol est àla pression atmosphérique.
14. D'après la loi de Jurin, jusqu'à quelle hauteur peut monter la sève ?
Si r = 10 µm, H ~1,5 m.
Le
contact entre la sève et l'atmosphère se fait à la surface des
feuilles, par des orifices ( stomates ) sur lesquels s'appuie le
ménisque et dont le rayon rs est plus petit que le rayon r des vaisseaux.
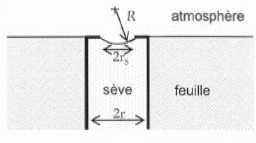
15.
La pression atmosphérique restant constante, comment évolue le rayon de
courbure R du ménisque si la pression au niveau de la feuille diminue
progressivement ?
- En déduire qu'il existe une valeur Pm de la pression de la sève dans les feuilles en dessous de laquelle le vaisseau est envahi par le gaz ( embolie).
Loi de Laplace : Patm-Psève = 2g / R.
Si Psève diminue alors R décroît progressivement jusqu'à ce que le ménisque soit hémisphérique ( R = rs).
Si la pression de la sève diminue encore, le rayon de courbure ne peut pas décroître et l'air envahit le vaisseau.
16. Exprimer Pm en fonction de rs, Patm et g. A.N : rs = 20 nm.
P0-Pm = 2g / rs ; Pm =P0 - 2g / rs ;
Pm = 105-2*0,073 / (20 10-9) ~ -7,2 106 Pa.
17. On considère un arbre de 20 m de hauteur.
On suppose que l'écoulement de sève dû à l'évaporation a un effet négligeable sur la pression.
Calculer la pression P en fonction de l'altitude z. Les vaisseaux remplis de sève sont-ils stables vis à vis de l'embolie ?
La variation de la pression de la sève suit la loi fondamentale de l'hydrostatique.
Psol -Pz = r g z.
Si Psol = 105 Pa ; Pz=20 m =105-1000*9,8*20 = -9,6 104 Pa.
Cette valeur étant inférieure au seuil de l'embolie, le vaisseau est stable vis à vis de l'embolie.
18.
Les mesures ci-dessous sont-elles compatibles avec le résultat
précédent ? Quelle hypothèse vous semble -t-elle la plus discutable ?
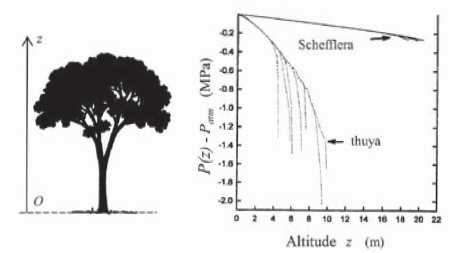
Le modèle précédent s'applique à l'espèce Schefflera mais pas au Thuya. Le modèle précédent est donc faux.
La sève n'est pas de l'eau pure. La sève s'écoule, il en résulte une perte de charge qui dépend beaucoup du réseau vasculaire.
19.
Ces mesures montrent que la sève est souvent à une pression négative.
En d'autres termes,il est possible de "tirer" sur de l'eau, comme sur
une corde, sans que l'eau ne "casse". Pourquoi est-ce possible pour un
liquide et non pour un gaz ?
Dans les liquides, des interactions
attractives entre molécules assurent la cohésion. Les liquides peuvent
résister à une tension.
|
|
|
|