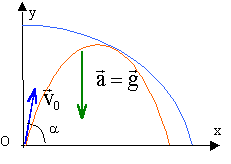
Interception d'une fusée balistique. Concours national Deug 2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Une fusée balistique, assimilée à un point matériel M pesant, est mise à feu à l’instant t = 0 depuis le point O avec une vitesse v0 faisant un angle a avec le plan horizontal ( O, x, z). La fusée se déplace uniquement dans le plan vertical (O, x, y). Le référentiel ℜ est considéré comme galiléen ; il est rapporté au repère ( O, x, y , z ). Appliquer le principe fondamental de la dynamique au point M. En déduire la relation vectorielle liant l’accélération du point M et l’accélération de la pesanteur.  Déterminer les équations paramétrées de la trajectoire du point M. En déduire l’équation de la trajectoire du point M.  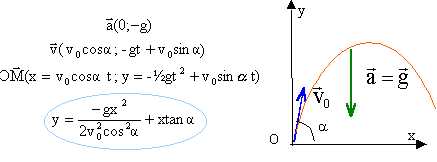En déduire la portée P et l’altitude maximale H atteinte par la fusée. Pour quelle valeur de a la portée P est-elle maximale ? Exprimer la portée maximale. Portée : y=0 0= -½gx²/(v0²cos²a) + x sin a / cosa. x= 0 ( origine de l'axe) ; -½gx/(v0²cosa) + sin a =0 donne x = 2v0²cosa sin a /g =v0² sin (2a) /g. La portée est maximale si : sin (2a) =1 soit a = p /4 ; Pmaxi =v0² /g. Flèche : La tangente à la trajectoire est horizontale ; la composante verticale de la vitesse est donc nulle. -gt +v0sina =0 soit t =v0sina /g repport dans y : H=-½ g(v0sina /g)² +v0sinav0sina /g =v0² sin ²a /(2g) La flèche est maximale si a = p /2 ( tir vertical) ; Hmaxi =v0² /(2g). On recherche l'ensemble des points atteints par ce projectile dont : - la valeur de la vitesse initiale est constante. - l'inclinaison a varie Donner l'équation de cette parabole. L'inconnue est dans ce cas l'angle a : 1/ cos² a =1+ tan²a : repport dans l'expression de la trajectoire. y = -gx² / 2v0²(1+ tan²a) + x tan a. tan²a + 2v0²/ (gx) tana +2v0² y / (gx²)-1 =0 il existe au moins une solution si le discriminant de cette équation du second degré est positif ou nul D' = v04/ (g²x²) -2v0² y / (gx²)+1 l'équation d e la courbe cherchée est : v04/ (g²x²) -2v0² y / (gx²)+1=0 soit y = -g /(2v0²) x² + v0² / (2g) parabole de sommet (0 : v0² / (2g)) . . On désire maintenant intercepter la fusée pendant le vol. Pour cela, on lâche sans vitesse initiale, à l’instant t1 positif, un obus au point N0 de coordonnées (x0, y0 , ). Cet obus sera assimilé à un point matériel N pesant. Déterminer les équations paramétrées de la trajectoire de l’obus. L'obus est en chute libre verticale : ax=0 ; ay = -g. Vitesse : vx=0 ; vy = -g(t-t1). Position : x = x0 ; y =-½g(t-t1)2+y0. En déduire à quel instant T s’effectue l’interception. x0 = v0 cos a T ; T = x0 / (v0 cos a ). En déduire une équation du second degré en t1 résultant de l’intersection des 2 trajectoires. -½g(T-t1)2+y0 = -½gT2 + v0sin a T. -½gT2+gTt1-½gt12+y0 = -½gT2 + v0sin a T. ½gt12-gTt1+ v0sin a T-y0=0. À quelle condition existe-t-il une solution à cette équation ? Où doit se situer le point N0 d’après cette condition ? Le discriminant doit être positif ou nul. D =(gT)2-2g(v0sin a T-y0) >=0 ; gT2-2v0sin a T+2y0 = 0 ; y0 =T(v0sin a -½gT). y0 =x0 / (v0 cos a )(v0sin a -½gx0 / (v0 cos a )). Déterminer à quel instant t1 l’obus doit être lâché afin de réussir l’interception. On retient la solution positive de l'équation du second degré. t1 = (gT±[(gT)2-2g(v0sin a T-y0)]½) / (½g). t1 = 2x0 / (v0 cos a )±2[ x20 / (v0 cos a )2-2 x0 tan a / g+2y0/g]½. . Un second projectile se déplaçe suivant l'hotizontale, à l'altitude v0² / (4g) à la vitesse 2v0. Déterminer l'angle de tir a pour que le premier projectile atteigne le second en tir tendu. Le second projectile est à t=0 au point d'ordonnée v0² / (4g). Sa vitesse est horizontale de valeur 2v0 orientée en sens contraire de l'axe des abscisses. Sa trajectoire est une droite horzontale d'ordonnée v0² / (4g). Son abscisse et son ordonnée vérifie l'équation : y = -g /(2v0²) x² + v0² / (2g) ; d'où l'abscisse à t=0 : v0² / (4g)= -g /(2v0²) x² + v0² / (2g) conduit à x0= v0² / (1,414g). L'abscisse en fonction du temps est : x2 = -2v0t + v0² / (1,414g). Au point d'impact ( en supposant qu'il existe) : D= ½( tan²a -1) positif si a >p/4. Le tir est tendu ; la solution cherchée est la plus petite racine de l'équation ci dessus. Le premier projectile se trouve en ce point I à la date : t = xI / (v0cosa). Le second projectile doit aussi s'y trouver : xI = -2v0 xI / (v0cosa) + v0² / (1,414g) xI = -2 xI / cosa + v0² / (1,414g) xI = v0²cosa / [1,414g(2+cosa)] égaler ces deux dernières expressions de xI : simplifier par v0²cosa /g. résolution à la calculatrice a = 74°.   .

menu