Exercice 1
: 2 / 20
On souhaite réaliser une source de tension de tension à vide 6 V à partir d'une source de tension de 9 V.
R1.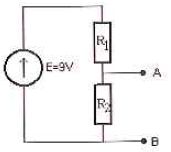 1.1
1.1. Donner le shéma équivalent de Thévenin vu à gauche entre les points A et B.
On retire la source E et on calcule la résistance de Thévenin :
R1 et R2 sont en parallèles : Rth =R1R2 / (R1+R2).
On laisse la source E et on met AB en court-circuit ; l'intensité I du courant est ICC = E / R1.
Fem du générateur équivalent de Thévenin ETh = Rth ICC= ER2 / (R1+R2).
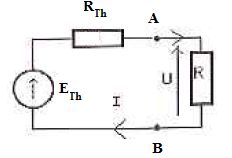
1.2.
On souhaite une tension à vide de 6 V et une résistance interne (
résistance de Thévenin ) de 50 ohms. Quelles sont les valeurs de R
1 et R
2.
R
1+R
2 = 50 et
6 *50 = 9R
2.
R2 = 33,3 ~33 ohms et R1 ~17 ohms.
Le schéma de Thévenin obtenu est associé à une résistance R.
1.3. La charge fonctionne avec une tension minimale Umini = 5 V. Quelles sont les valeurs de R admissibles ?
U doit être comprise entre 5 et 6 V.
U = Eth R / (R+Rth) ; U(R+Rth) = Eth R ; R = URth / (Eth-U).
Pour Umini : Rmini =5*50 /(6-5) = 250 ohms.
R doit être supérieure à 250 ohms.
1.4. Exprimer la puissance dissipée dans R en fonction de E
th, R
th et R. En déduire la valeur de R rendant P maximale.
P = U I =
E2th R / (R+Rth)2.
On dérive P par rapport à R et on annule cette dérivée.
u = E2th R ; u' =E2th ; v = (R+Rth)2 ; v' = 2(R+Rth).
Dérivée d'un quotient : 0 = u'v-v'u = E2th (R+Rth)2 -2(R+Rth) E2th R.
R+Rth =2R ; R = Rth.