Math�matiques, Brevet, Inde 2018.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

.
.
Exercice 1 . ( 13 points ).
On consid�re un jeu constitu� d'un plateau tournant et d'une boule. Ce plateau comporte 13 cases num�rot�es de 0 � 12. la boule a la m�me probabilit� de s'arr�ter sur chaque case.
1. Quelle est la probabilit� que la boule s'arr�te sur la case n� 8 ?
Un seule cas favorables parmi 13 possibilit�s, donc : 1 / 13 ~0,077.
2. Quelle est la probabilit� que le num�ro de la case sur lequel s'arr�te la boule soit un num�ro impair ?
Six cas favorables ( 1, 3, 5, 7, 9, 11) sur 13 possibilit�s, soit 6 / 13 ~0,46.
3. Quelle est la probabilit� que le num�ro de la case sur lequel s'arr�te la boule soit un nombre premier ?
Six cas favorables ( 1, 2, 3, 5, 7, 11) sur 13 possibilit�s, soit 6 / 13 ~0,46.
4. Lors des deux derniers lancers, la boule s'est arr�t�e � chaque fois sur la case num�ro 9. A t-on maintenant plus de chances que la boule s'arr�te sur la case num�ro 9 plut�t que sur la case num�rot�e 7 ? Argumenter.
La boule a la m�me probabilit� de s'arr�ter sur chaque case, quel que soit le r�sultat des lancers pr�c�dents.
Probabilit� d'arr�t sur le num�ro 9 = probabilit� d'arr�t sur le num�ro 7 = 1  / 13. R�ponse : non.

 Exercice 2 ( 9 points ).

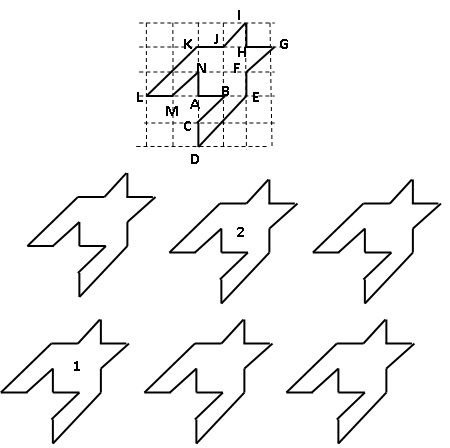
1. Quel type de  transformation g�om�trique permet d'obtenir le motif 2 � partir du motif 1 ? Une translation..
2. Dans cette question AB = 1 cm. D�terminer l'aire de ce motif.
Aire du carr� AEHK : 2 x2 = 4 cm2.
Aire des 8 triangles du type IJH : 8 x1 x1 /2 = 4 cm2.
Aire du motif : 8 cm2.
3. Marine affirme " si je divise par 2 les longueurs d'un motif, son aire sera ausi divis�e par 2" A t-elle raison ? Expliquer pourquoi ?
Une aire est �gale au produi d'une longueur par une longueur. Si chaque longueur est divis�e par 2, l'aire est divis�e par 4. Marine a tord.

.
.


Exercice 3. ( 9 points ) QCM.
1. 2,53 1015 =2 530 000 000 000 000.  R�ponse B.
2. La latitude de l'�quateur est : 0 ( vrai) ; 90� est ; 90� nord ; 90� sud..
3.
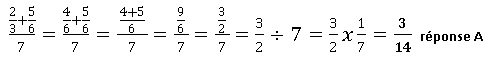
Exercice 4 ( 18 points).
Programe A :
Choisir un nombre.
Soustraire 3.
Calculer le carr� du r�sultat obtenu		 Programme B.
Choisir un nombre.
Calculer son carr�.
Ajouter le triple du nombre de d�part.
Ajouter 7.
1. Corinne choisit le nombre 1 et applique le programme A. Expliquer en d�taillant les calculs que le r�sultat est 4.
1 ; 1-3 = -2 ; (-2)2 = 4.
2. Tidjane choisit le nombre -5 et applique le programme B. Quel r�sultat obtient-il ?
(-5)2 = 25 ; 25 +(-15) = 10 ; 10+7 = 17.
3. Lina souhaite regrouper le r�sultat dans un tableur.

3. Quelle formule, copi�e ensuite � droite dans les cellules C3 � H3 a t-elle saisie dans la cellule B3 ?
=B1*B1+3*B1+7.
4. Zo� cherche � obtenir le m�me r�sultat pour les deux programmes. Elle note x le nombre de d�part.
4.1. Montrer que le r�sultat du programme a peut s'�crire  : x2-6x+9.
(x-3)2= x2-6x+9.
4.2. Ecrire le r�sultat du programme B en fonction de x.
x2+3x+7.
4.3 Existe-t-il un nombre de d�part pour lequel les deux programmes donnent le m�me r�sultat ? Si oui, lequel ?
x2-6x+9 = x2+3x+7.
-6x+9 = 3x+7.
9-7=3x+6x
2=9x
x=2 / 9.
 .
..
..



Exercice 5 . (20 points ).


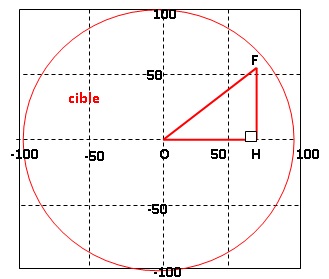
On lance une fl�chette sur une cible. Si la pointe est sur le bord de la cible, on consid�re que la cible n'est pas atteinte.
Longueur de la plaque carr�e : 200 mm ; rayon de la cible : 100 mm. La pointe de la fl�che est repr�sent�e par le point F.
1. Coordonn�es du point F ( 72 ; 54 ). Montrer que OF = 90 mm.
Le triangle OHF est rectangle en H.
OF2 = OH2 +FH2 = 722 +542 =8100 ; OF = 90 mm.
2. Quel nombre ne doit pas d�passer la distance OF pour que la fl�chette atteigne la cible ?
OF < 100 mm.
3. On r�alise un programme qui simule plusieurs fois le lancer de la fl�chette et qui compte le nombnre de lancers atteignant la cible. Le programmeur a cr�� trois variaables nomm�es : carr� de OF, distance et score.

D�part.
Mettre score �  z�ro.
R�p�ter 120 fois.
   Aller �  : x : nombre al�atoire entre -100 et +100 ; y : nombre al�atoire entre -100 et +100.
    Mettre carr� de OF � abscisse x fois abscisse x +.......  .........
Mettre distance � racine de ......
Si distance < .... alors
ajouter 1 � score.
Fin r�p�ter.
a. Combien de lancers sont simul�s ? 120.
b. Quel est le r�le de la variable score ?
Score donne le nombre de lancers atteignant la cible.
c. Compl�ter le programme afin qu'il fonctionne correctement.
    Mettre carr� de OF � abscisse x fois abscisse x +ordonn�e y fois ordonn�e y.
Mettre distance � racine de carr� de OF.
Si distance < 100 alors
3. Apr�s ex�cution du programme, la variable score est �gale � 102. A quelle fr�quence la cible a-t-elle �t� atteinte dans cette simulation ? Exprimer le r�sultat sous forme d'une fraction irr�ductible.
102 / 120 = 51 / 60 = 17 / 20.
4. La probabilit� d'atteindre la cible est �gale au quotient : aire de la cible divis�e par aire du carr�. Donner cette probabilit� au centi�me pr�s.
pr2 / cot�2 =3,14 x1002 / 2002 = 3,14 / 4 ~0,79.


Exercice 6 ( 15 points).
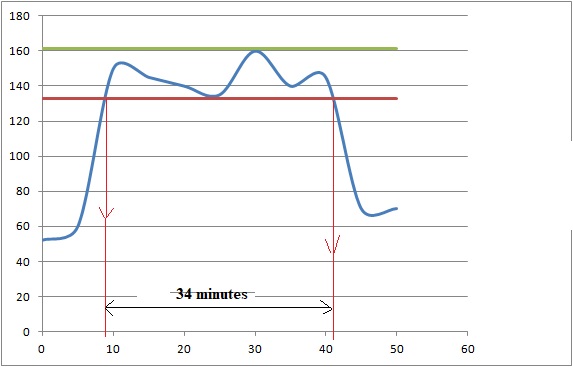
Chris fait une course de v�lo tout terrain. le graphe ci-dessous repr�sente la fr�quence cardiaque ( nombre de battements par minute) en fonction du temps.

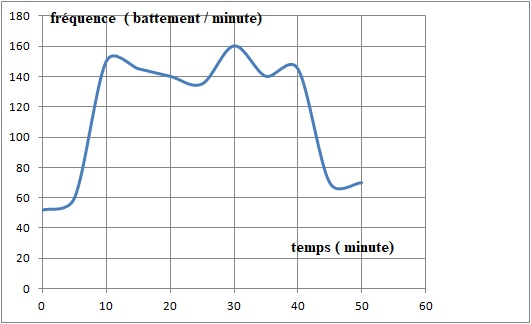
1. Quelle est la fr�quence cardiaque de Chris au d�part de la course ? ~ 52.
2. Quelle est la fr�quence maximale atteinte au cours de la course ? 160.
3. Chris est parti � 9 H 33 de chez lui et termine sa course � 10 h 26. Quelle a �t� la dur�e en minutes de sa course ?
27 +26 = 53 minutes.
4. Chris a parcouru 11 km. Montrer que sa vitesse moyenne est d'environ 12,5 km /h.
11 / 53 x60 = 12,45 ~12,5 km / h.
5. La fr�quence maximale  ( FCM) de Chris est de 190 battements par minute. L'effort est soutenu si la fr�quence  cardiaque mesur�e est comprise entre 70 et 85 % de la FCM.
Estimer la dur�e de la p�riode pendant laquelle Chris a fourni un effort soutenu.
190 x0,70 = 133 ; 190 x0,85 = 161,5.

Exercice 7. ( 16 points).

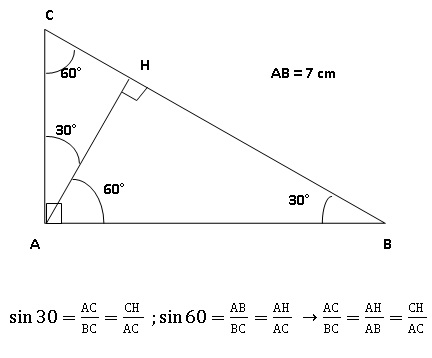
1. Tracer la figure en vrai grandeur.
2. Montrer que AH = 3,5 cm.
Dans le triangle rectangle AHB : sin 30 = AH / AB ; AH = AB sin 30 = 7 x0,5 = 3,5 cm.
3. D�montrer que les triangles ABC et HAC sont semblables.
Ces deux triangles sont des triangles demi �quilat�raux.
sin 30� = AC / BC = CH / AC ; sin 60� = AB / BC =AH / AC ( voir ci-dessus)..
4. D�terminer le coefficient de r�duction permettant de passer du triangle ABC au triangle HAC.
AH / AB = 3,5 / 7 =0,5.


  

menu