Chasse
au plomb,
concours Concours commun polytechnique 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Trajectoires des plombs d'une cartouche.
Un
fusil de chasse (arme à feu) ou de ball-trap permet d’envoyer à
distance des projectiles au moyen de gaz produits par la combustion
rapide et confinée d’un composé chimique. La déflagration va éjecter de
la bouche du fusil les sphères de plomb qui étaient dans la cartouche
avec une vitesse qui, enmoyenne, vaut v0 = 380 m. s−1, valeur à utiliser dans toutes les applications numériques ultérieures.
Nous considérons la trajectoire d’un plomb de cartouche dont la
dimension est typiquement de quelques millimètres et la masse
inférieure au gramme. On néglige la poussée d’Archimède.
Équation du mouvement.
Le projectile est a priori soumis à deux forces : son poids et la force
de frottement fluide exercée par l’air qui, dans les cas considérés,
est constituée de la traînée aérodynamique qui s’écrit :
FD = 0,5 raSCDv2.
où v est la norme du vecteur vitesse du projectile, ra est la masse volumique de l’air, S = pR2 est la section de l’objet exposée au fluide dans la direction de l’écoulement et CD
est un coefficient sans dimension appelé « coefficient de traînée ».
Pour les vitesses typiques étudiées (vitesses supersoniques situées
entre 375 et 420 m/s) et pour les formes quasi-sphériques de
projectiles, CD est de l’ordre de 0,44.
Q1. Établir l’équation différentielle du mouvement du centre de masse du plomb de masse m.
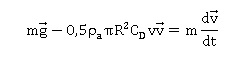
On confondra, par la suite, le plomb avec une masse ponctuelle à laquelle on appliquera la force de trainée aérodynamique.
Premier modèle : trajectoire gravitaire.
On considère le cas où la vitesse initiale du projectile est
suffisamment faible pour que l’on puisse négliger la force de
frottement fluide de l’air.
Q2. Montrer que cela correspondrait à une vitesse initiale v0, obéissant à l’inégalité :
v0 << [2mg / (rapR2CD)]½.
La norme de la force de trainée est négligeable devant la valeur du poids.
0,5 raSCDv02<< mg ; v02<< 2mg / (rapR2CD).
Par la suite on notera voo= [2mg / (rapR2CD)]½.
Q3. Projeter l’équation du mouvement sur la base cartésienne. L'’origine O est la position de la particule à l’instant initial.
Q4. Établir les équations paramétriques de la vitesse et de la position en fonction du temps.
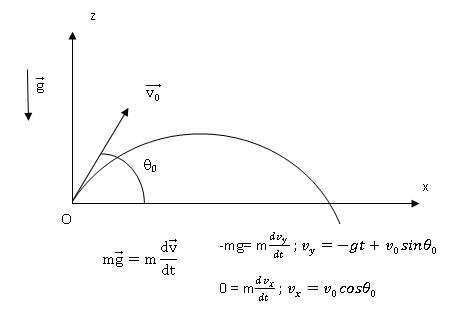
Q5. Quelle est la nature de cette trajectoire dite « gravitaire » ?
z = -½gt2 + v0 sin q0 t ; x = v0 cos q0 t .
Eliminer le temps : z = -½gx2 / ( v0 cos q0)2 +tan q0 x . La trajectoire est parabolique.
Q6. Montrer
que la portée du tir, c’est-à-dire la distance atteinte par le
projectile dans le plan horizontal de départ (Z = 0), vaut
XM =v02 sin (2q0) /g et que la hauteur maximale atteinte par le projectile vaut HM = v02 sin2 (q0) / (2g).
z=0 conduit à : -½gxM2 / ( v0 cos q0)2 +tan q0 xM =0.
xM =0 ; 0,5gxM / ( v0 cos q0)2 =sin q0 /cos q0.
xM =2v02sin q0 cos q0 / g = v02 sin (2q0) /g.
La composante verticale de la vitesse est nulle lorsque la hauteur maximale est atteinte :
-gt +v0sin q0 =0 ; t = v0sin q0 / g.
HM = -½g(v0sin q0 / g)2 + v0 sin q0 v0sin q0 / g =v02 sin2 (q0) / (2g).
Q7. Donner la valeur de l’angle q0 pour laquelle la portée est maximale.
sin (2q0) = 1 soit q0= p / 4.
Q8. Application numérique
La taille des plombs est identifiée par un numéro allant de 1 à 12 qui
correspond à une régression arithmétique des diamètres de 0,25 mm par
numéro. Une cartouche de n° 8 possède des plombs plus petits qu’une de
n° 4. Le tableau 1 ci-dessous donne les rayons de quelques types de
plombs et certains résultats numériques obtenus en utilisant les
formules ci-dessus pour une vitesseinitiale v0 = 380 m.s-1. Compléter le tableau. rplomb = 11350 kg m-3.
n° du plomb
|
1
|
5
|
10
|
Rayon (mm)
|
2,0
|
1,5
|
0,875
|
Masse (g)
|
0,38
|
0,16
|
0,031
|
Portée ( km)
|
15
|
Hauteur maxi (km)
|
3,7
|
voo (m/s)
|
33
|
29
|
22
|
Masse = 4 / 3 p R3 rplomb = 4 / 3 x3,14 x(1,5 10-3)3 x11350 = 1,60 10-4 kg = 0,16 g.
XMaximale =v02 /g=3802 /9,81=14,7 103 m =14,7 km.
HMaximale = v02 sin2 (q0) / (2g) =(380 xsin 45)2 /(2 x9,81) = 3680 m = 3,68 km.
voo = [2mg / (rapR2CD)]½=[2 x0,1610-3 x9,81 / (1,23x3,14x0,00152x0,44)]½ =28,65 m/s.
Q9. Comparer la portée maximale, obtenue pour un angle θ0
= 45°, à la portée donnée (diamètre des plombs × 100 = zone dangereuse
en m. Exemple : pour des plombs de 1,5 mm : 1,5 × 100 = 150 m.)
et conclure. Quel(s) autre(s) facteur(s) montre(nt) qu’il faut
abandonner le modèle gravitaire ?
La portée maximale indiquée par le fabriquant est très inférieure à celle trouvée dans ce modèle.
Dans ce modèle la portée ne dépend pas de la masse.
De plus la force de frottement fluide n'est pas négligeable devant le poids.
|
|
|
Deuxième modèle : trajectoire de Tartaglia.
On vient de voir dans l’étude précédente que, pour les plombs de chasse, v0 est très supérieure à voo.
Dans ce cas, la trajectoire diffère considérablement de la trajectoire gravitaire. On distingue 3 phases :
une première phase à mouvement rectiligne, une deuxième phase à
trajectoire asymétrique autour d’un sommet et une troisième phase de
mouvement de chute verticale. Il s’agit d’une « trajectoire de
Tartaglia », du nom du mathématicien balisticien Niccolò Tartaglia
(XVIe siècle), qui a décrit les trajectoires d’un boulet de canon.
Phase initiale : mouvement rectiligne ascendant.
Soit OX’ la direction de la droite trajectoire dans cette phase
initiale. On note X’ l’abscisse du point M sur cette droite qui fait un
angle θ0 avec OX et v sa vitesse.
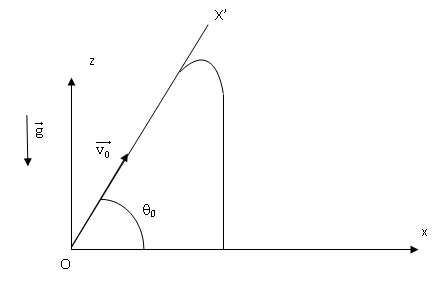
Q10. Montrer que le poids d’un plomb est alors négligeable devant la force de traînée.
v0 est très supérieure à voo : v02>> 2mg / (rapR2CD).
mg << 0,5 v02rapR2CD.
Q11. Montrer que l’équation du mouvement dans la première phase se met sous la forme :
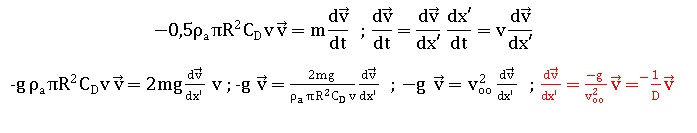
Q12. Quelle est la dimension de D ?
D est le carré d'une vitesse divisée par une accélération. D a la dimension d'une longueur.
Q13. Établir l’expression de v en fonction de X’.
Que représente le paramètre D
dv / v = - dx' / D ; ln v = - x' / D + constante ;
Lorsque x' = 0, v = v0, d'où : ln v = -x' / D + ln v0 ; ln ( v / v0) = - x' / D ; v = v0 exp( -x' / D).
D représente la distance caractéristique d'atténuation de la vitesse.
Q14. On note d la distance que doit parcourir le plomb pour atteindre une vitesse 10 voo, vu la vitesse atteinte quand le plomb a parcouru 40 m et Ec
l’énergie cinétique correspondante. Le tableau ci-dessous donne pour
trois numéros de plomb des résultats numériques obtenus en utilisant
les formules ci-dessus pour une vitesse initiale v0 = 380 m.s-1.
n° du plomb
|
1
|
5
|
10
|
D(m)
|
110
|
84
|
50
|
v0 / voo
|
11
|
13
|
17
|
d (m)
|
15
|
24
|
27
|
vu (m/s)
|
270
|
236
|
170
|
Ec(J)
|
13,5
|
4,4
|
0,45
|
Compléter par des valeurs à deux chiffres significatifs.
D = g / voo2 = 28,652 / 9.81 =83,67 ~84 m.
v0 / voo=380 /28,65 =13,26~13.
10voo = v0 exp( -d / D) ; d=D ln(v0 / (10voo)) = 83,67 ln(380 /286,5) =23,63 m.
vu =380 exp(-40 /83,67)=235,6 ~236 m/s.
Ec = ½mv2u =0,5 x1,6 10-4 x235,62 =4,44 J.
Q15. Comment définiriez-vous la portée utile d’un tir ?
La portée est la projection horizontale d'une trajectoire courbe en trois dimensions.
La portée utile est de l'ordre de grandeur de D.
On lit dans les journaux de chasse que le caractère mortel du tir vient
en première approximation du fait que les plombs qui pénètrent dans le
gibier communiquent à l’animal leur énergie cinétique créant ainsi une
onde de choc fatale.
Q16. En supposant
qu’il suffit de 2 plombs numéro 1 pour avoir un canard à son tableau de
chasse, de combien de plombs 5 et 10 suffirait-il ? En déduire l’ordre de grandeur de la portée utile à l’aide de l’évaluation du paramètre D précédemment défini.
Energie cinétique de 2 plombs n°1 : 13,5 x2 = 27 J.
Nombre de plomb n°5 nécessaire : 27 / 4,44 ~6.
Nombre de plomb n°10 nécessaire : 27 / 0,45 ~60.
L'énergie des plombs à une distance égale à la portée utile doit être de l'ordre de 13,5 J.
La vitesse des projectiles est donc de l'ordre de : (2 x13,5 / 3,8 10-4)½ =266 m /s.
La portée utile est de l'ordre de : 84 ln(380 / 266) ~ 30 m.
Q17. Comparer aux valeurs données dans le document 1 (35 à 40 m).
La portée utile calculée est du même ordre de celles données.
Pourquoi faut-il prendre des billes plus grosses en fer doux, sachant qu’il s’agit d’un acier de masse volumique 7 600 kg.m–3 ?
Ec = ½mv2 =0,5 mv02exp(-2portée / D) ; 2 portée / D = ln ( 0,5 mv02/ Ec).
Portée = 0,5 D ln ( 0,5 mv02/ Ec). La portée varie avec le logarithme de la masse.
L'acier a une masse volumique inférieure à celle du plomb. Pour une
masse égale ( donc la même portée), les billes d'acier doivent avoir un
rayon plus grand que celles de plomb.
Quel est le danger lié à l’agglutination de la grenaille ?
Les billes agglutinées constituent des projectiles d’un poids supérieur
qui peuvent être dangereux à des distances beaucoup plus grandes.
Troisième et dernière phase : mouvement rectiligne descendant.
On note que cette phase est quasiment verticale.
Q18. À quoi correspond-elle ?
Mouvement rectiligne vertical uniforme au cours duquel l'accélération est négligeable.
Q19. Montrer que la vitesse limite atteinte pendant cette dernière phase vaut : voo= [2mg / (rpR2CD)]½.
La bille de plomb est soumise à son poids, verticale vers le bas,
valeur mg et à la force de frottement fluide, verticale vers le haut,
valeur 0,5 rapR2CDv2.
Lorsque la vitesse limite est atteinte, ces deux forces se compensent.
mg =0,5 rapR2CDvlim2.
Expliquer le terme de « mur aérodynamique » utilisé pour qualifier cette dernière phase.
La bille de plomb ne peut plus accélérée, sa vitesse est constante.
|
|
|
|
Deuxième phase : la phase intermédiaire
Dans cette phase, la vitesse a diminué.
Q20. Pourquoi qualifie-t-on cette phase de « phase gravitaire » ?
Dans la partie 1, le poids était négligeable; dans la partie 3, l'accélération est négligeable.
Dans la partie intermédiaire le plomb est soumis à son poids et à la force de frottement.
Le poids n'est pas négligeable, d'où le qualificatif " gravitaire ".
On peut établir par un calcul formel, à partir de l’équation du
mouvement, l’expression approchée de la portée maximale du projectile
pour ce type de trajectoire :
XM ≈ D cos q0 / 2 ln[1 +4 (v0/voo)2 sin q0] = h cotan q0.
Q21. Évaluer numériquement les portées maximales des numéros 1, 5 et 10 de plombs, pour θ0 = 16°.
Comparer aux valeurs données dans le document 1 (pages 2-3).
n° du plomb
|
1
|
5
|
10
|
Diamètre (mm)
|
4
|
3
|
1,75
|
v0 / voo
|
11
|
13
|
17
|
D (m)
|
110
|
84
|
50
|
XM(m)
|
258
|
216
|
138 |
Portée proposée document 1 : 100 fois diamètre
|
400
|
300
|
175
|
Les valeurs données dans le document et celles calculées sont du même ordre de grandeurs.
De plus la portée dépend de la masse. Si la masse augmente, la portée croït.
Le même calcul donne également l’expression approchée de l’angle initial permettant d’optimiser la portée maximale XM.
Q22. La figure suivante donne la courbe θmax, (en degrés) fonction de log(v0 / voo)2. Identifier la valeur de θmax pour les trois numéros de plomb considérés.
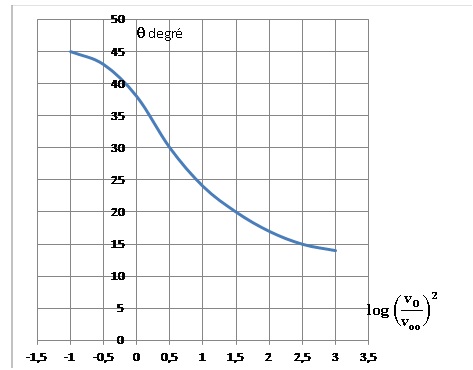
n° du plomb
|
1
|
5
|
10
|
v0 / voo
|
11
|
13
|
17
|
log(v0 / voo)2.
|
2,1
|
2,23
|
2,46
|
qmax(degré)
|
17
|
16
|
15 |
Pour calculer plus précisément la portée utile du tir de grenaille de plomb, on intègre numériquement l’équation du mouvement.
La figure suivante donne les trajectoires des plombs n° 1, 5 et 10 de vitesse initiale 380 m.s–1, pour l’angle θ0 optimisant la portée maximale. Les valeurs des coordonnées et des rayons sont en mètres.
Q23. Évaluer les portées maximales pour chaque calibre et comparer aux données du document 1
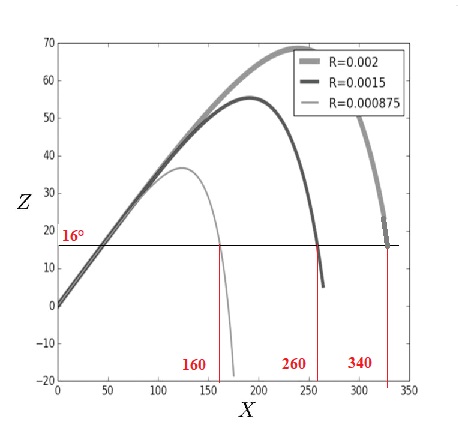
|
|
|