Mathématiques,
fonction, probabilités, suites, géométrie,
Bac S Antilles 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
Les trois parties de cet exercice sont indépendantes.
Dans tout l’exercice, les résultats seront arrondis, si besoin, à 10−3.
Partie A.
Elsa a préparé un grand saladier de billes de chocolat pour son
anniversaire. On y trouve :
• 40% de billes au chocolat blanc, les autres étant au chocolat noir ;
• parmi les billes au chocolat blanc, 60% sont fourrées au café; les
autres sont fourrées au praliné;
• parmi les billes au chocolat noir, 70%sont fourrées au café; les
autres sont fourrées au praliné.
Un invité prend une bille de chocolat au hasard dans le saladier. On
définit les évènements suivants :
• B : « l’invité prend une bille au chocolat blanc » ;
• C : « l’invité prend une bille fourrée au café ».
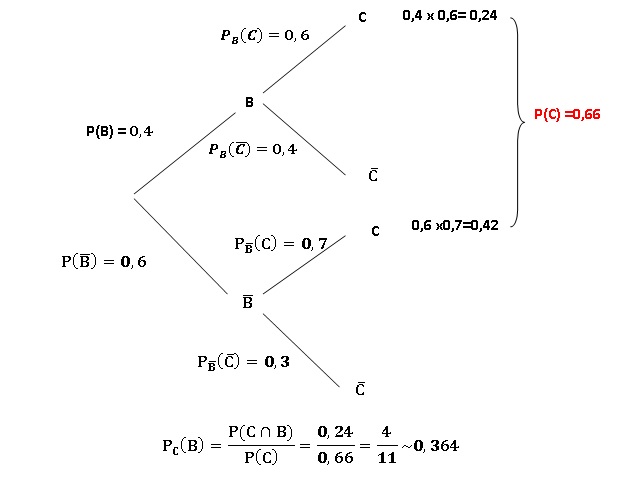
1. Représenter la
situation à l’aide d’un arbre de probabilités.
2. Montrer que la
probabilité que l’invité prenne une bille fourrée au café vaut 0,66.
3. Sachant que la
bille est fourrée au café, quelle est la probabilité que l’invité ait
pris une bille au chocolat blanc ?
Partie B.
La société Chococéan commercialise des bonbons au chocolat, qui sont
conditionnés en paquets d’environ 250 g par une machine. La
réglementation exige qu’un tel paquet de bonbons au chocolat ait une
masse supérieure à 247,5 g.
La dirigeante de l’entreprise constate que, lorsqu’on prélève au hasard
un paquet de bonbons au chocolat dans la production, sa masse, en
grammes, peut être modélisée par une variable aléatoire X1
qui suit une
loi normale d’espérance μ1 = 251 et d’écart-type s = 2.
1. Calculer la
probabilité qu’un paquet prélevé au hasard dans la production soit
conforme à la réglementation.
.P(X1
> 247,5)= 1- P(X1
<
247,5) = 1-0,0401=0,960
2. La dirigeante
souhaiterait que 98% des paquets soient conformes à la réglementation.
Cela nécessite un nouveau réglage de la machine, afin que la masse, en
grammes, du paquet prélevé au hasard soit modélisée par une variable
aléatoire X2 qui suit une loi normale d’espérance μ2
inconnue et d’écart-type s=
2. Déterminer la valeur de μ2 répondant au souhait de la
dirigeante.
On pose Z = (X2-µ2) / 2 ; Z suit la loi normale centrée réduite.
P(X2 > 247,5 ) = 0,98 ; P(247,5 < X2 < µ2) +0,5 = 0,98.
P(247,5 < X2 < µ2) = 0,48.
P(247,5-µ2 < X2 -µ2 < 0) = 0,48.
.P(X2
> 247,5)= 1- P(X2
<
247,5) = 0,980 ; µ2 = 251,6.
Partie C.
La société procède à un réglage de la machine. La dirigeante affirme
que désormais 98% des paquets produits sont conformes à la
réglementation.
Une association de consommateurs fait peser 256 paquets de bonbons au
chocolat et en dénombre 248 qui sont conformes à la réglementation.
Le résultat de ce contrôle remet-il en question l’affirmation de la
dirigeante ? Justifier la réponse.
n = 256 > 30 ; p = 0,98 ; np =250,88 > 5 ; n(1-p) = 5,12
> 5.
Les
conditions sont réunies pour définir un intervalle de fluctuation au
seuil de 95 %.
1,96 [(p(1-p) / n]½
= 1,96 x[0,98 x0,02
/ 256]½ = 0,01715.
I = [0,98-0,017 ; 0,98 +0,017] soit [0,963 ; 0,997].
La fréquence observée 248 / 256 = 0,967 appartient à cet intervalle.
L'affirmation n'est pas remise en cause.
|
|
Exercice 2.
On note R l’ensemble des nombres réels.
Partie A.
Soit f2 la fonction définie sur R par f2(x) = (x
+2)e−x .
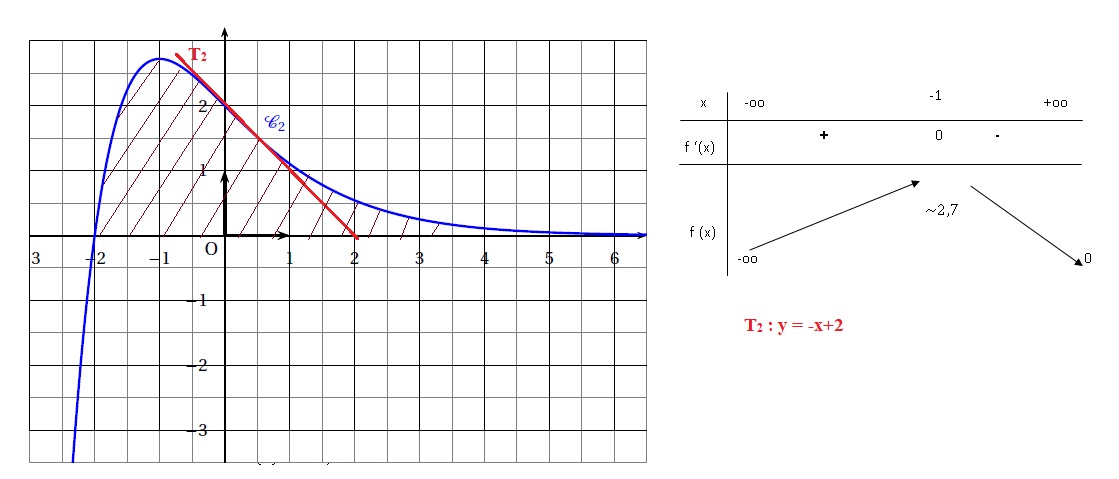
La courbe représentative de f2, notée C2 est
tracée dans un repère orthonormé.
Aucune justification ni aucun calcul ne sont attendus dans cette partie.
1. Conjecturer les
limites de f2 en moins l'infini et plus l'infini.
En moins l'infini, la fonction tend vers moins l'infini; en plus l'infini, la fonction tend vers zéro.
2. Conjecturer le
tableau de variations de f2 à l’aide du graphique.
3. Soit T2
la tangente à la courbe C2 au point d’abscisse 0. Tracer
cette tangente, puis en conjecturer une équation par lecture graphique.
4. Hachurer un
domaine dont l’aire est donnée par l’intégrale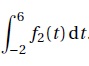
Partie B.
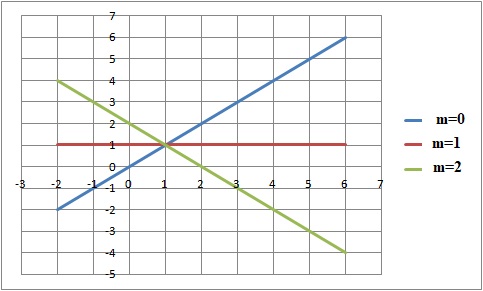
Pour tout réel m, on note fm la fonction définie sur R par fm(x)
= (x +m)e−x et Cm sa courbe représentative dans un repère orthonormé.
1. Calculer les
limites de fm en moins l'infini et plus l'infini.
Quand x tend vers plus l'infini : e-x tend vers zéro ; x+m tend vers plus l'infini et fm(x) tend vers zéro.
Quand x tend vers moinss l'infini : e-x tend vers plus l'infini ; x+m tend vers moins l'infini et fm(x) tend vers moins l'infini.
2. On admet que fm
est dérivable sur R et on note f ′m sa dérivée.
Montrer que, pour tout réel x, f ′m (x) = (−x −m+1)e−x
.
On pose u = x+m et v = e-x ; u' = 1 ; v' = -e-x ; u'v + v'u = e-x-(x+m)e-x =(−x −m+1)e−x
.
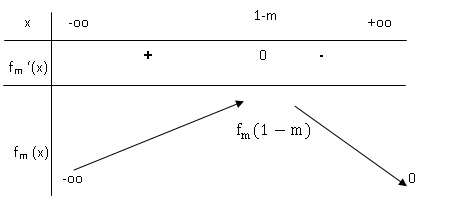
3. En déduire les
variations de fm sur R.
4. a. Pour tout
réel m, on note Tm la tangente à la courbe Cm au
point d’abscisse 0. Démontrer que Tm a pour équation
réduite y = (1−m)x +m.
Coefficient directeur de cette tangente : fm'(0) =-m+1.
Equation de cette tangente : y = (-m+1)x+b.
La tangente passe par le point d'abscisse zéro et de coordonnée fm(0) =m. Par suite b = m.
b. Démontrer que
toutes les droites Tm passent par un même point dont on
précisera les coordonnées.
Les coordonnées de ce point doivent être indépendantes de m.
Pour x = 1, y est indépendant de m et vaut 1. le point cherché a pour coordonnées (1 ; 1).
5. Étudier le signe
de fm(x) pour tout réel x.
e−x est toujours positif ; si x > -m, fm(x) est positive ; si x < -m, fm(x) est négative ; si x = -m, fm(x) est nulle.
6. On admet que la
fonction F2 définie sur R par F2(x) = −(x +3)e−x
est une primitive de f2 sur R.
a. Déterminer, en
fonction de x, l’expression de 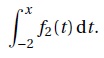
F2(x) - F2(-2) = −(x +3)e−x + (-2 +3)e2 =−(x +3)e−x +e2 .
b. En déduire la
valeur de 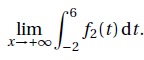
Quand x tend vers plus l'infini : e-x tend vers zéro, -(x+3) tend vers moins l'infini et −(x +3)e−x tend vers zéro.
La limite cherchée est e2.
|
|
Exercice 3.
On considère un cube ABCDEFGH. La figure est donnée ci-dessous. AB =AD=AE = 1
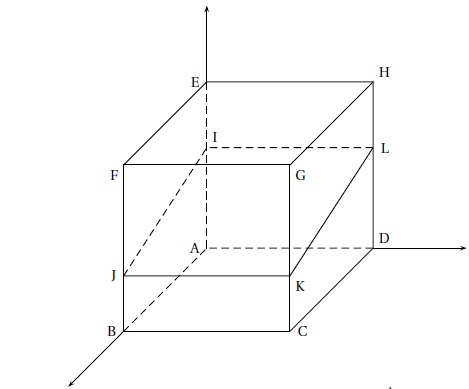
On note P1 le plan d’équation 4x +15z −9 = 0.
La section IJKL du cube ABCDEFGH par le plan P1 est
représentée sur la figure.
1. Déterminer les
coordonnées des points I et J.
I appartient à l'axe AE : I(0 ; 0 ; zI).
I appartient au plan P1 : 15 zI-9 = 0 soit zI =9 / 15 = 3 / 5 = 0,6. I(0 ; 0 ; 0,6).
J appartient au plan ABE : J(xJ ; 0 ; zJ).
J appartient à la droite BF, donc xJ = 1.
J appartient au plan P1 : 4 xJ+15 zJ-9 = 0.
4 +15 zJ-9 = 0 ; zJ = 1 /3. J(1 ; 0 ; 1/3).
2. Le plan P1
partage le cube en deux prismes. Calculer le volume de chacun de ces
deux prismes.
Volume du prisme inférieur : aire du trapèze ABIJ fois hauteur AD.
V1 = (BJ +AI) x AB / 2 = (1 / 3 + 3 / 5) / 2 = 7 / 15.
Volume du prisme supérieur : volume du cube - V1 = 1 - 7 / 15 = 8 / 15.
3. Soit M un point
du segment [EI].
On cherche un plan P2 parallèle à P1 et passant
par M qui partage le cube en deux prismes de même volume.
Déterminer une équation cartésienne de P2 .
Les deux plans étant parallèles, l'équation cartsienne de P2 est de la forme : 4x +15z -d = 0 avec d réel.
Coordonnées du point I'(0 ; 0 ; z).
I' appartient au plan P2 : 15 z - d = 0 ; z = d / 15.
Coordonnées du point JI'(1 ; 0 ; z').
J' appartient au plan P2 : 4+15 z' - d = 0 ; z' = (d-4) / 15.
Volume du prisme inférieur : aire du trapèze ABI'J' fois hauteur AD.
V1 = (BJ' +AI') x AB / 2 ; BJ' =(d+4) / 15 ; AI' = d / 15.
V1 = (2d-4) / 30 = 0,5 ; soit d = 9,5.
Equation du plan P2 : 4x +15z -9,5 = 0.
Exercice 4.
On considère la suite (un) définie par u0 = 1, et
pour tout entier naturel n, un+1 = e×un½.
1. Démontrer par
récurrence que, pour tout entier naturel n, 1 < un < e2.
Initialisation : la propriété est vraie pour n = 0.
Hérédité : la propriété est supposée vraie au rang n : 1 < un < e2.
1 < un½ < e ; puis multiplier par e : e < eun½ < e2 ; e < un+1 < e2 .
e < un+1 donc 1 < un+1.
Or 1 < e donc 1 < un+1 < e2.
La propriété étant vraie au rang zéro et héréditaire, elle est vraie pout tout entier naturel.
.2. a. Démontrer que
la suite (un) est croissante.
un+1-un = e×un½-un=un½(e-un½).
un½ est positif et un < e2, donc
un+1-un > 0.
un+1 > un, la suite est croissante.
b. En déduire la
convergence de la suite (un).
La suite étant croissante et bornée ( majorée) , elle converge.
3. Pour tout entier
naturel n, on pose vn = ln(un)−2.
a. Démontrer que la
suite (vn) est géométrique de raison 0,5.
vn+1 = ln(un+1)−2.
vn+1 = ln(e×un½)−2 =ln(e) +0,5 ln(un)-2 =1 +0,5 ln(un)-2 = 0,5 ln(un)-1=0,5( ln(un)-2)=0,5 vn.
La
suite (vn) est géométrique de raison 0,5.
b. Démontrer que,
pour tout entier naturel n, vn = −1/ 2n−1 .
v0 = ln(u0)-2 = ln(1)-2 = -2.
vn = v0 x1 / 2n = -2 x1 / 2n = −1/ 2n−1 .
c. En déduire une
expression de un en fonction de l’entier naturel n.
vn = ln(un)−2 ; vn +2 =2-1 / 2n−1= ln(un).
un = exp(vn+2)= exp [ 2-1 / 2n−1].
d. Calculer la
limite de la suite (un).
Quand n tend vers plus l'infini : 0 < 1 /2 < 1, donc (1 / 2)n-1 tend vers zéro.
un tend vers e2.
4. Dans cette
question, on s’interroge sur le comportement de la suite (un)
si l’on choisit d’autres valeurs que 1 pour u0.
Pour chacune des affirmations ci-dessous, indiquer si elle est vraie ou
fausse en justifiant.
Affirmation 1 : « Si u0 = 2018, alors la suite (un)
est croissante. ». Faux.
u0 = 2018 ; u1 = e x2018½ ~122, valeur inférieur à u0.
Affirmation 2 : « Si u0 = 2, alors pour tout entier naturel
n, 1 < un
< e2.
» Vrai.
1 < u0 < e2.
On reprend l'hérédité du raisonnement ( question 1).
Affirmation 3 : « La suite (un) est constante si et
seulement si u0 = 0. » Faux.
On doit résoudre l'équation x = e x½ soit x2 = e2x ; x2-e2x = 0.
Cette équation possède deux solutions x =0 et x = e2.
En choisissant x = e2 : u1 =e u0½ = e2 = u0, la suite est constante.
|
|