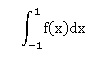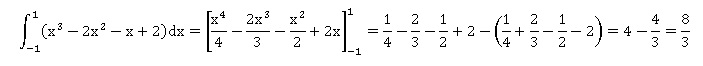Mathématiques, bac Stl biotechnologies Nlle Calédonie 2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . ...... ..... Exercice 1.6 points. Partie A : Questionnaire à choix multiples. Pour chaque question, une seule des réponses proposées est exacte. Chaque bonne réponse rapporte un point, une mauvaise réponse ou l’absence de réponse n’enlève pas de point. Aucune justification n’est demandée. 1. Soit la fonction f définie sur R par f (x) = (3x2 +4)e2x−1. La fonction f ′ dérivée de f est donnée par : a. f ′(x) = 6xe2x−1. On pose u = 3x2+4 et v = e2x-1 ; u' = 6x ; v' = 2e2x-1. u'v +v'u = 6xe2x-1 +2(3x2+4)e2x-1 = (6x2++6x+8)e2x-1 . b) f ′(x) = 6x ×ln(2x −1) c) f ′(x) = (6x2 +6x +8)e2x−1. Vrai. d) f ′(x) = 12xe2x−1. 2. On considère l’équation différentielle suivante (E) : 2y′−3y = 1. Une solution f de (E) est donnée par : a. f (x) = 2018e1,5x-0,5. Solution générale de 2y'-3y=0 : y = A e1,5x avec A une constante. Solution particulière de (E) : y = -1/3. Solution générale de (E) : y = A e1,5 x -1/3. b. f (x) = e-1,5x -0,5. c. f (x) = 2018e-3x+0,5. d. f (x) = e1,5x +0,5. PARTIE B. On a tracé la courbe C représentative d’une fonction f définie sur R ainsi que la tangente T à C au point d’abscisse 0. 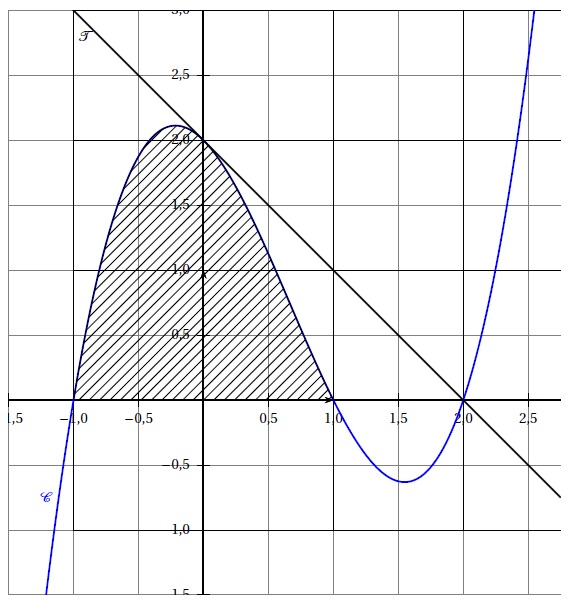1. Déterminer graphiquement une équation de la tangente T à la courbe C au point d’abscisse 0. y = a x+b avec a et b des constantes. le point de coordonnées (0 ; 2) appartient à la tangente : b = 2. Coefficient directeur de la tangente : -1. y = -x+2. 2. a. Déterminer graphiquement les solutions de l’équation f (x) = 0. x = -1 ; x=1 ; x=2. b. Dresser le tableau de signes de la fonction f sur [−1 ; 2,5]. Sur ]1 ; 2 [, f(x) est strictement négative ; sur ]2  ; 2,5 ), f(x) est strictement positive. 3. Exprimer l’aire, en unité d’aire, du domaine hachuré  à l’aide d’une intégrale. 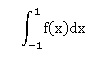PARTIE C. On admettra, dans la suite, que la fonction étudiée dans la partie B est définie sur R par f (x) = x3 −2x2 −x +2. 1. Déterminer, par le calcul, les valeurs de f (0) et f ′(0). Retrouver une équation de la tangente T à la courbe C au point d’abscisse 0. f(0) =2. f '(x) = 3x2-4x-1. f '(0) = -1. Equation de la tangente T : y = f '(0) x + f(0) = -x +2. 2. a. 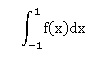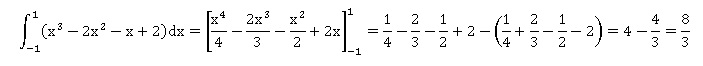Déterminer, en détaillant les calculs, la valeur exacte de b. Interpréter ce résultat dans le contexte de l’exercice. L'aire du domaine hachurée est égale à 8 / 3 unités d'aire. ... Exercice 2. 5 points. Le métabolisme de base d’un organisme correspond aux besoins énergétiques incompressibles de l’organisme, c’est à- dire l’énergie minimale quotidienne permettant à l’organisme de survivre. Il dépend essentiellement de la taille, du poids, de l’âge, du sexe. Le tableau ci-dessous donne, en fonction de l’âge, le métabolisme de base en kcal (kilocalorie) d’une femme mesurant 1,60 met pesant 55 kg : Age  ti ( année) 23 27 34 40 48 62 Métabolisme de bas mi ( kcal) 1325 1297 1259 1233 1204 1165 ln(ti) 3,1 3,3 3,5 3,7 3,9 4,1 ln(mi) 7,19 7,17 7,14 7,12 7,09 7,06 1. On effectue les changements de variable : xi = ln(ti ) et yi = ln(mi ) où ln désigne la fonction logarithme népérien. a. Compléter le tableau . 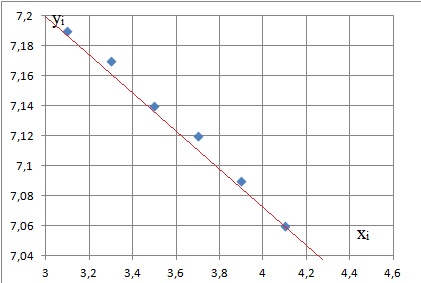b. Représenter le nuage de points de coordonnées (xi ; yi ) . Pourquoi un ajustement affine est-il envisageable ? Les points paraissent alignés. c. Déterminer une équation de la droite D d’ajustement de y en x obtenue par la méthode des moindres carrés sous la forme y = ax +b (Arrondir a à 10−2 près et b à 10−3 près). y = -0,13 x +7,596. d. Représenter cette droite D dans le repère. 2. a. Démontrer, à partir de l’équation obtenue à la question l. c., que m ≈ 1990×t−0,13. ln(m) = -0,13 ln(t) +7,596 ; ln(m) = -0,13 ln(t) + ln(1990)= ln(t-0,13) +ln(1990) = ln (1990 t-0,13) ; m = 1990 t-0,13. b. Donner une estimation, arrondie à 1 kcal, du métabolisme de base de cette femme à 70 ans. m = 1990 x 70-0,13=1146 kcal. c. À quel âge, arrondi à 1 an, son métabolisme de base était-il de 1 180 kcal ? t-0,13 = 1180 / 1990 = 0,593 ; -0,13 ln(t) = ln(0,593) ; ln(t) ~ 3,98 ; t ~54 ans. 3. La formule de Black et al. et les besoins caloriques quotidiens a. De nos jours, la formule de Black et al. (1996) est la formule de référence pour une estimation de la valeur du métabolisme de base exprimée en kcal. Pour une femme, la formule est : m = 230×p0,48 ×h0,5 ×t−0,13 où m est le métabolisme de base en kcal, p est la masse en kg, h est la taille en m et t est l’âge en année. La formule établie en 2. a. donnant le métabolisme de base d’une femme mesurant 1,60 m et pesant 55 kg est-elle cohérente avec la formule de Black et al. ? 230 x 550,48 x1,600,5 = 1991. Les formules sont cohérentes. b. Les besoins caloriques quotidiens moyens dépendent du métabolisme de base et de l’activité; aussi pour les calculer, on multiplie le métabolisme de base par 1,37 pour des femmes sédentaires, par 1,55 pour des femmes actives et par 1,80 pour des femmes sportives. Calculer les besoins caloriques quotidiens, arrondis à 1 kcal, d’une lycéenne sportive âgée de 17 ans mesurant 1,72 m et pesant 60 kg. m = 1,80 x230 x600,55 x1,720,5 x17-0,13 =3571 kcal. .... Exercice 3. 5 points. La dureté d’une eau est liée à la présence de calcaire dans le sous-sol. Plus une eau est calcaire, plus elle est riche en calcium. Une usine produit de l’eau minérale en bouteilles. Lorsque le taux de calcium dans une bouteille dépasse 60 mg par litre, on dit que l’eau de cette bouteille est moyennement dure ou calcaire. Partie A : Loi binomiale. Dans un stock important de bouteilles, 7% des bouteilles contiennent de l’eau calcaire. On prélève au hasard 75 bouteilles dans le stock pour vérifier la concentration en calcium. Le stock est suffisamment important pour que l’on puisse assimiler ce prélèvement à un tirage avec remise de 75 bouteilles. On note X la variable aléatoire qui donne le nombre de bouteilles d’eau calcaire de ce prélèvement. 1. Justifier que la variable aléatoire X suit une loi binomiale, de paramètres n = 75 et p = 0,07. Les prélèvements sont indépendants et il y a deux issues possibles ( l'eau est calcaire ou ne l'est pas). X suit une loi binomiale de paramètres n = 75 et p = 0,07. 2. Quelle est la probabilité que, lors d’un tel tirage, il y ait 5 bouteilles d’eau calcaire? p(X =5) = 0,180. 3. Quelle est la probabilité que, lors d’un tel tirage, il y ait 65 bouteilles d’eau non calcaire ? Il y a donc 10 bouteilles d'eau calcaire : P(X =10) = 0,021. 4. Calculer P(X < 10) et interpréter le résultat. P(X < 10) = 0,985. La probabilité de tirer au plus 10 bouteilles d'eau calcaire est égale à 0,985. Partie B : Approximation de la loi binomiale par une loi normale. On souhaite approcher la variable aléatoire X définie en partie A par une variable aléatoire Y suivant une loi normale. 1. a. Les conditions n >30, np >5 et n(1−p)>5 sont-elles vérifiées pour la variable aléatoire X ? n =75 > 30 ; np = 75 x0,07 = 5,25 > 5 ; n(1-p) = 75 x0,93=69,75 > 5. Les conditions sont vérifiées. b. Montrer que Y suit la loi normale d’espérance 5,250 et d’écart-type 2,210. Espérance µ=np = 5,25 ; écart type s = (np(1-p))½ = (75 x0,07 x0,93)½ =2,210. 2. Calculer P(Y < 10). P(Y < 10) = 0,984. Au regard de la question A. 4, ce résultat était-il prévisible? Justifier la réponse. Ce résultat était prévisible, les conditions n >30, np >5 et n(1−p)>5 étant vérifiées 3. Déterminer, en utilisant la loi de Y , la probabilité approchée d’avoir entre 3 et 5 bouteilles d’eau calcaire. P(Y < 5) =0,455 ; P(Y < 3) =0,154 ; P 3 < Y < 5) = 0,455 -0,154 ~0,301. Partie C : Intervalle de fluctuation asymptotique. Dans cette question, on s’intéresse à la concentration en calcium de l’eau d’une grande quantité de bouteilles devant être livrées à une chaîne d’hypermarchés. Le fournisseur affirme qu’il y a dans son stock 6% de bouteilles d’eau calcaire. On prélève au hasard et avec remise un échantillon de 100 bouteilles dans cette livraison. 1. Déterminer l’intervalle de fluctuation asymptotique à 95% de la fréquence des bouteilles d’eau calcaire dans un échantillon de 100 bouteilles prélevées comme indiqué ci-dessus. 1,96 (p(1-p) / n)½ = 1,96(0,06 x0,94 / 100)½ ~ 0,0465. Intervalle de fluctuation asymptotique [ 0,06 -0,0465 ; 0,06 +0,0465] soit [0,013 ; 0,107]. 2. Dans l’échantillon prélevé, il y a 8 bouteilles d’eau calcaire. Peut-on remettre en cause l’affirmation du fournisseur ? Justifier la réponse. La fréquence 8 /100 = 0,08 appartient à cet intervalle. L'affirmation n'est pas remise en cause.   Exercice 4. 4 points. En région Île de France, les alertes à la pollution atmosphérique se multiplient. Le décret du 21 octobre 2010 relatif à la qualité de l’air et un arrêté inter-préfectoral de 2016 définissent les procédures d’information-recommandations et d’alerte du public en cas d’épisode de pollution. - si la concentration en ozone est supérieure ou égale à 180 μg.m-3 et strictement inférieure à 240 μg m−3, la procédure d’information-recommandations est déclenchée ; - si la concentration en ozone est supérieure ou égale à 240 μg m−3 et strictement inférieure à 300 μg.m−3, le premier seuil d’alerte est déclenché. - si la concentration en ozone est supérieure ou égale à 300 μg m−3 et strictement inférieure à 360 μg.m−3, le second seuil d’alerte est déclenché. Les mesures en cas d’alerte visent à réduire les émissions de gaz à effet de serre et donc la concentration d’ozone. L’abaissement de la vitesse autorisée sur les voies de circulation est une de ces mesures. Ces mesures permettent, en théorie, de réduire de 12,5% la concentration d’ozone par jour. Le 17 juillet, en Île de France, on relève une concentration d’ozone de 330 μg. m−3. Une alerte est déclenchée et les mesures sont activées. Dans la suite, on modélise l’évolution de cette concentration d’ozone après activation des mesures. 1. Vérifier que, selon ce modèle, la concentration en ozone le 18 juillet sera de 288,75 μg.m−3. 330 x(1-0,125) =330 x0,875 =288,75 μg.m−3. 2. À quelle date le premier seuil d’alerte sera-t-il levé en suivant ce modèle ? 330 x0,875n < 240 ; 0,875n < 240 / 330 ; 0,875 n < 0,727. n ln(0,875) < ln(0,727) ;  n > 2,38 soit n = 3 jours. 3. On donne l’algorithme ci-dessous : n←0 C ←330 Tant que C > 180 n←n +1 C ←C ×0,875 Fin Tant que Quelle est la valeur de n à la fin de l’exécution de l’algorithme ? Interpréter le résultat dans le contexte de la partie A. 330 x0,875n < 180 ; 0,875n < 180 / 330 ; 0,875 n < 0,545. n ln(0,875) < ln(0,545) ;  n > 4,54 soit n = 5 jours. Au bout de 5 jours, la procédure d'information-recommandations est annulée. 4. Pour la protection de la santé humaine, l’objectif de qualité à atteindre est une concentration d’ozone inférieure ou égale à 120 μg.m−3. Recopier et modifier l’algorithme précédent afin qu’il détermine le nombre de jours nécessaires pour atteindrel’objectif. Donner ce nombre de jours. n←0 C ←330 Tant que C > 120 n←n +1 C ←C ×0,875 Fin Tant que 330 x0,875n < 120 ; 0,875n < 120 / 330 ; 0,875 n < 0,364. n ln(0,875) < ln(0,364) ;  n > 7,58 soit n = 8 jours. Partie B : Les particules fines PM10. Le seuil d’information-recommandations aux particules fines PM10 en suspension (diamètres inférieurs ou égaux à 10 μm) est fixé à 50 μg.m−3 d’air et le seuil d’alerte à 80 μg.m−3. À proximité de l’autoroute A7, les relevés suivants de particules fines PM10 en suspension ont été effectués : 13 juillet 2017 : 213 μg.m−3 ; 14 juillet 2017 : 16 μg. m−3. 1. Pour chaque date, préciser si un seuil a été dépassé et si oui, préciser ce seuil. Le 13 juillet le seuil d'alerte à 80 µg m-3 est largement dépasé. Le 14 juillet le seuil d'information-recommandations de 50 µg m-3 n'est pas atteint. 2. a. Quel est le pourcentage de baisse observée de la concentration en particules fines PM10 entre le 13 et le 14 juillet 2017 ? On arrondira le pourcentage à 10−2 près. (213-16) / 213 x100 = 92,49 %.  b. Proposer une explication à cette baisse. Beaucoup de circulation de voitures le 14 juillet, jour de grand départ,  et très peu le jour suivant.

menu