Mathématiques,
concours audioprothésiste Nancy 2014
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
I. 8 points.
Soient les nombres complexes a et z0 définis ci-dessous.
z0 = 6+6i d'image A0.
Pour tout entier naturel non nul, on désigne par An le point d'affixe zn défini par : zn = an z0.
Partie A.
1. Exprimer z1 et a2 sous forme algébrique.
Ecrire z1 sous forme exponentielle et montrer que a2 = 0,5 exp(ip/6).
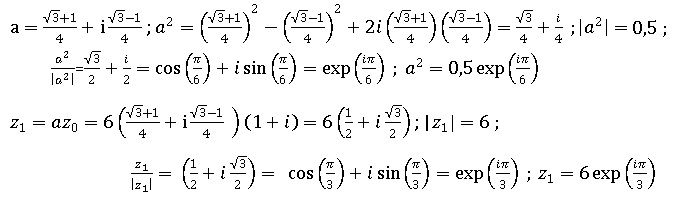
2. Exprimer z3 puis z7 en fonction de a2 ; en déduire l'expression de z3 et z7 sous forme exponentielle.
z3 = a3 z0 = a2 az0 = a2 z1 =0,5 exp(ip/6) x 6 exp(ip/3)= 3exp(ip/6+ip/3) =3 exp( ip/2).
z7 = a7 z0 = (a2 )3az0 = (a2 )3 z1 =0,53 exp(ip/2) x 6 exp(ip/3)= 0,75 exp(ip/2+ip/3) =0,75 exp( i5p/6).
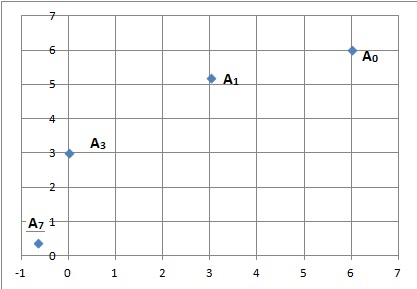
3. Placer les points A0, A1, A3 et A7, images respectives des complexes z0, z1, z3 et z7.
|
|
Partie B.
Pour tout entier naturel on pose |zn| = rn.
1. Montrer que, pour tout entier naturel :
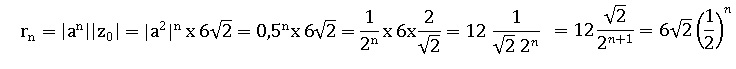
2. En déduire que la suite (rn)n est géométrique dont on précisera le premier terme et la raison.
Il s'agit d'une suite géométrique de premier terme 6 x2½ et de raison 0,5.
3. Déterminer la limite de cette suite et interpréter.
0 < 0,5 <1, donc 0,5n tend vers zéro quand n tend vers plus l'infini.
La limite de cette suite est égale à zéro.
rn-rn-1 = 6 x 2½[ 0,5n -0,5n-1]=6 x 2½[ -0,5n ] ;
rn-rn-1 <0, la suite est décroissante.
La suite étant décroissante et minorée par zéro, elle converge.
II. 1,5 points.
Résoudre dans R l'équation :
ln(x) +ln(x-6) +ln(x-3) = ln(4x).
ln(x) est défini pour x strictement positif.
ln(x-6) est défini pour x >6 ; ln(x-3) est défini pour x >3 ; cette expression est définie pour x > 6.
ln[x(x-6)(x-3)] = ln (4x).
x(x-6)(x-3) = 4 x.
(x-6)(x-3) = 4.
x2-9x+14 = 0.
D = 81-4x14 =25.
x1 =(9+5) / 2 = 7 ; x1 =(9-5) / 2 = 2 ne convient pas.
|
|
III. 4 points.
Calculer les dérivées par rapport à la variable x des fonctions :
y1 = sin(1/x2).
On pose u = 1 / x2 ; u' = -2 / x3 ; y1' = -2 / x3 cos(1/x2).
y2 = x /(x-1).
On pose u = x et v = x-1 ; u' = 1 ; v' = 1.
(u'v-v'u) / v2 = (x-1-x) / (x-1)2 = -1 / (x-1)2.
y3 = x tan (x2).
on pose u = x2 ; u' = 2x ; dérivée de : tan (u) = u' / cos2(u) =2x / cos2(x2) .
Puis dérivée d'un produit :
v = x ; w = tan(x2) ; v' = 1 ; w' = 2x / cos2(x2).
v ' w + w ' v =tan(x2)+ 2x2 / cos(x2).
y4 = x½ cos (x-½).
On pose u = x-½ ; u' = -0,5 x-1,5.
Dérivée de cos (u) = -u' sin (u) = 0,5 x-1,5sin(0,5 x-1,5sin(x-½).
Puis dérivée d'un produit :
v = x½ ; w = cos (x-½) ; v' = 0,5 x-½ ; w' = 0,5 x-1,5sin( x-½).
v ' w + w ' v =0,5 x-½cos (x-½)+x½ 0,5 x-1,5sin(x-½).
IV. 3 points.
Calculer les intégrales :
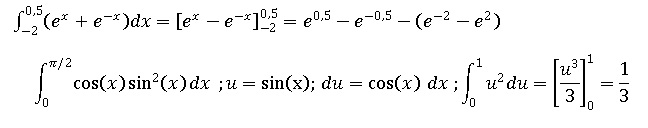
V. 3,5 points.
Déterminer la limite quand x tend vers plus l'infini de :
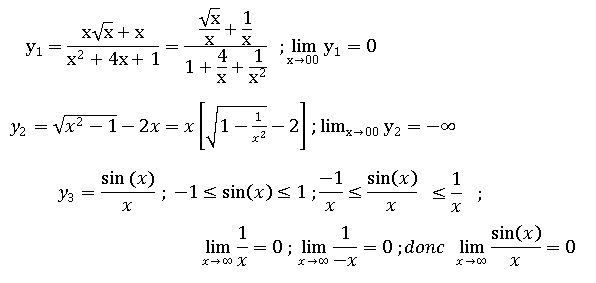
|
|