Mathématiques,
bac S Antilles septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
| .
. |
......
.....
|
Exercice 1. 5 points
Les trois parties de l’exercice peuvent être traitées indépendamment.
Une association offre à ses adhérents des paniers de légumes. Chaque adhérent a le choix entre trois tailles de panier :
• un panier de petite taille;
• un panier de taille moyenne;
• un panier de grande taille.
Partie A.
L’association envisage de proposer en outre des livraisons d’oeufs
frais. Pour savoir si ses adhérents sont intéressés, elle réalise un
sondage. On interroge un adhérent au hasard. On considère les
évènements suivants :
• A : « l’adhérent choisit un panier de petite taille » ;
• B : « l’adhérent choisit un panier de taille moyenne » ;
• C : « l’adhérent choisit un panier de grande taille » ;
• F : « l’adhérent est intéressé par une livraison d’oeufs frais ».
On dispose de certaines données, qui sont résumées dans l’arbre ci-dessous :
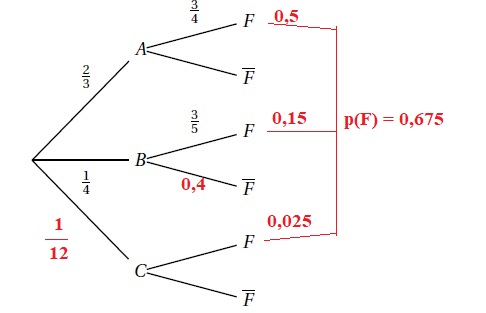
1. Dans cette question, on ne cherchera pas à compléter l’arbre.
a. Calculer la probabilité que l’adhérent choisisse un panier de petite taille et soit intéressé par une livraison d’oeufs frais.
2 / 3 x3 /4 = 0,5.
b. Calculer P(B n non F), puis interpréter ce résultat à l’aide d’une phrase.
1 /4 x(1-3 /5) =1 / 4 x 2 / 5 =0,1.
10 % des adhérents choisissant un panier de taille moyenne envisage d'acheter des oeufs frais.
c.
La livraison d’oeufs frais ne sera mise en place que si la probabilité
de l’évènement F est supérieure à 0,6. Pourquoi peut-on affirmer que
cette livraison sera mise en place ?
La probabilité qu'un client achetant un petit panier ou un panier moyen achète des oeufs vaut :
0,5 +1/4 x3 /5 =0,5 +0,15 = 0,65, valeur supérieure à 0,6.
2. Dans cette question, on suppose que P(F)= 0,675.
a. Démontrer que la probabilité conditionnelle de F sachant C, notée PC (F), est égale à 0,3.
La formule des probabilités totales conduit à : P(C n F) = 0,675 -0,5 -0,15 =0,025.
PC (F) =0,025 / (1 /12) =0,025 x12 = 0,3.
b. L’adhérent interrogé est intéressé par la livraison d’oeufs frais.
Quelle est la probabilité qu’il ait choisi un panier de grande taille ? Arrondir le résultat à 10−2.
PF(C) = P(C n F) / P(F) =0,025 / 0,675 =0,037.
Partie B.
1. La masse, en
gramme, d’un panier de grande taille peut être modélisée par une
variable aléatoire, notée X, suivant une loi normale d’espérance 5 000
et d’écart- type 420. Un panier de grande taille est déclaré non
conforme lorsque sa masse est inférieure à 4,5 kg.
On choisit au hasard un panier de grande taille.
Quelle est la probabilité, arrondie au centième, qu’il soit non conforme ?
P(X < 4,5) =0,117~0,12.
2. Les responsables
de l’association décident de modifier la méthode de remplissage. Avec
cette nouvelle méthode, la masse, en gramme, d’un panier de grande
taille est désormais modélisée par une variable aléatoire, notée Y ,
suivant une loi normale d’espérance 5 000 et d’écart-type σ. La
probabilité qu’un panier de grande taille choisi au hasard soit non
conforme est alors de
0,04. Déterminer la valeur de σ arrondie à l’unité.
σ = 286 grammes.
Partie C.
Depuis plusieurs années, les associations distribuant des produits
frais à leurs adhérents se développent dans tout le pays et connaissent
un succès grandissant.Lors d’une émission de radio consacrée à ce
sujet, un journaliste annonce que 88% des adhérents de ces associations
sont satisfaits.
Un auditeur intervient dans l’émission pour contester le pourcentage
avancé par le journaliste. A l’appui de son propos, l’auditeur déclare
avoir réalisé un sondage auprès de 120 adhérents de ces associations et
avoir constaté que, parmi eux, seuls 100 ont indiqué être satisfaits.
La contestation de l’auditeur est-elle fondée ?
n=120 ; p= 0,88 ; 1-p =0,12.
n = 120 > 30 ; np = 100 > 5 ; n(1-p) =20 > 5.
On peut définir un intervalle de fluctuation asymptotique.
1,96 [p(1-p) / n ]½ =1,96 (0,88 x0,12 / 120)½ =0,058.
Intervalle de fluctuation asymptotique [ 0,88-0,058 ; 0,88 +0,058 ] soit [0,822 ; 0,938 ].
La fréquence observée 100 / 120 = 0,833 appartient à cet intervalle. La contestation n'est pas fondée.
|
...
|
|
Exercice 2. 5 points.
L’espace est rapporté à un repère orthonormé.
On considère les points A(10; 0; 1), B(1; 7; 1) et C(0; 0; 5).
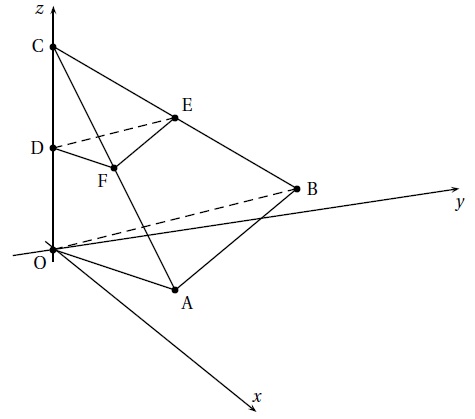
1. a. Démontrer que les droites (OA) et (OB) ne sont pas perpendiculaires.
b. Déterminer la mesure, en degré, de l’angle AOB, arrondie au dixième.

2. Vérifier que 7x +9y −70z = 0 est une équation cartésienne du plan (OAB).
A appartient à ce plan : 7x10 +9 x0 -70 x1 =0 est vérifié.
B appartient à ce plan : 7x1 +9 x7 -70 x1 =0 est vérifié.
0 appartient à ce plan : 7x0 +9 x0 -70 x0 =0 est vérifié.
3. Déterminer une représentation paramétrique de la droite (CA).
Coordonnées d'un vecteur directeur de cette droite : (10 ; 0 ; -4).
C (0 ; 0 ; 5) appartient à cette droite :
x = 10 t +xC ; y = 0+yC ; z = -4t +zC avec t réel
x = 10 t ; y = 0 ; z = -4t+5.
4. Soit D le milieu du segment [OC]. Déterminer une équation du plan P parallèle au plan (OAB) passant par D.
D(½xC ; ½yC ; ½zC). D(0 ; 0 ; 2,5).
Le plan P est parallèle au plan (OAB) ; son équation est : 7x +9y −70z +d= 0
D appartient à ce plan P : 7 x0 +9 x0 -70 x 2,5 +d = 0 soit d = 175.
7x +9y −70z +175= 0.
5. Le plan P coupe la droite (CB) en E et la droite (CA) en F.
Déterminer les coordonnées du point F. On admet que le point E a pour coordonnées (0,5 ; 3,5 ; 3).
F appartient au plan P : 7xF +9yF −70zF +175= 0.
F appartient à la droite (CA) : xF = 10 t ; yF = 0 ; zF = -4t +5 avec t réel.
70 t+ 9 x0 -70(-4t+5) +175 = 0.
350t -175 =0 ; t =0,5.
xF = 5 ; yF = 0 ; zF = 3.
6. Démontrer que la droite (EF) est parallèle à la droite (AB) .
Coordonnées d'un vecteur directeur de la droite (EF) :
(5-0,5 ; 0-3,5 ; 3-3) soit ( 4,5 ; -3,5 ; 0).
Coordonnées d'un vecteur directeur de la droite (AB) :
(1-10 ; 7-0 ; 1-1) soit (-9 ; 7 ; 0).
Ces deux vecteurs étant colinéaires, les droites sont parallèles.
...........
|
...
.
|
....
|
Exercice 3. 5 points.
Soit g la fonction définie sur ]0 ; +∞[ par
g (x)= 4x −x ln x.
On admet que la fonction g est dérivable sur ]0 ; +∞[ et on note g ′ sa dérivée.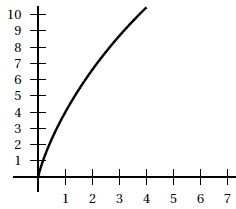
Partie A.
Le graphique ci-dessus représente une partie de la courbe
représentative de la fonction g obtenue par un élève sur sa
calculatrice. Cet élève
émet les deux conjectures suivantes :
• il semble que la fonction g soit positive;
• il semble que la fonction g soit strictement croissante.
L’objectif de cette partie est de valider ou d’invalider chacune de ces conjectures.
1. Résoudre l’équation g (x) = 0 sur l’intervalle ]0 ; +∞[.
x(4-ln(x))=0 ; solution retenue : ln(x) = 4 soit x =e4 ~55.
2. Déterminer le signe de g (x) sur l’intervalle ]0 ; +∞[.
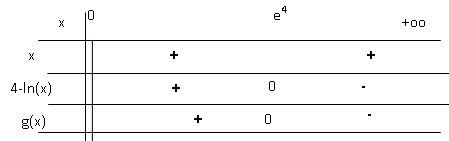
3. Les conjectures de l’élève sont-elles vérifiées ?
La première conjecture est vérifiée sur l'intervalle ]0 ; 6].
La fonction g ne peut pas être strictement croissante. La seconde conjecture est fausse.
Partie B.
Dans cette partie, on poursuit l’étude de la fonction g .
1. a. On rappelle que la limite en plus l'infini de ln(t) / t est égale àzéro.
En déduire que la limite en zéro de x ln(x) est égale à zéro.
ln (-x) = ln (1/x) ; x = 1 / (1/x) ; on pose t = 1/x ; -x ln(x) = -ln(t) / t.
Quand x tend vers 0+, t tend vers +oo et ln(t) / t tend vers zéro.
b. Calculer la limite de g (x) lorsque x tend vers 0.
4x tend vers zéro ; xln(x) tend vers zéro ; g(x) tend vers zéro.
2. a. Démontrer que, pour tout réel x strictement positif, g ′(x) = 3−lnx.
On pose u = x ; v = ln(x) ; u' = 1 ; v' = 1/x ; (uv)' = u'v+v'u = ln(x) +1.
g'(x) = 4-ln(x) -1 = 3 -ln(x).
b. Dresser le tableau de variations de la fonction g.
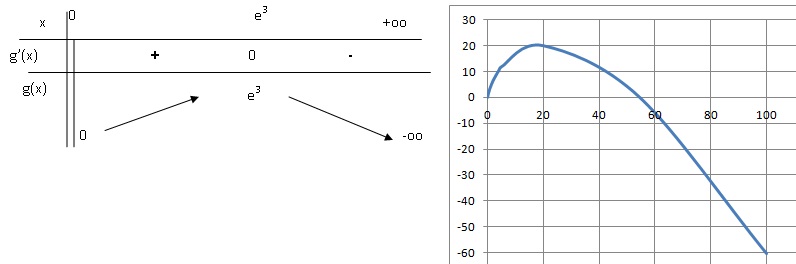
3. On désigne par G la fonction définie sur ]0 ; +∞[ par
G(x) =0,25 x2 (9-2ln(x))
On admet que la fonction G est dérivable sur ]0 ; +∞[.
a. Démontrer que la fonction G est une primitive de la fonction g sur ]0 ; +∞[.
On dérive G en posant u = 0,25 x2 et v = 9-2ln(x) ; u' =0,5x ; v' = -2 /x.
u'v+v'u = 0,5x(9-2ln(x)) -0,5x =0,5x(8-2ln(x) = x(4-ln(x)) = g(x).
b. L’affirmation suivante est-elle vraie?
« Il n’existe aucun réel α strictement supérieur à 1 tel que :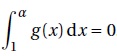
G(a) -G(1) =0,25 a2 (9-2ln(a))-2,25 =0.
a2 (9-2ln(a))- 9 =0 ; affirmation fausse.

|
Exercice 4. 5 points
Les parties A et B de cet exercice sont indépendantes.
Partie A.
Pour chacune des trois affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse.
Il est attribué un point par réponse correctement justifiée. Une
réponse non justifiée n’est pas prise en compte, une absence de réponse
n’est pas pénalisée.
1. On considère la suite (pn) définie pour tout entier naturel n, par
pn = n2 −42n +4.
Affirmation 1 : La suite (pn) est strictement décroissante. Faux.
pn+1 -pn= (n+1)2 −42(n+1) +4 -( n2 −42n +4)
pn+1 -pn=(n+1)2 −n2 -42 .
pn+1 -pn=(n+1+n)(n+1-n) -42 =(2n+1)-42 = 2n -41.
pn+1 -pn > 0 si n >20,5 ( suite croissante) et pn+1 -pn < 0 si n < 20,5 ( suite décroissante).
2. Soit a un nombre réel. On considère les suites (un) et (vn) définies par :
• U0 = a et, pour tout entier naturel n, un+1 =(u2n+8)½ /3.
• vn = u2n−1 pour tout entier naturel n.
Affirmation 2 : La suite (vn) est une suite géométrique. Vrai.
vn+1 = u2n+1−1 =(u2n+8) / 9-1 =u2n/ 9-1 /9 =(u2n-1) / 9 = vn /9.
(vn) est une suite géométrique de premier terme a2-1 et de raison q =1/9.
3. On considère une suite (wn) qui vérifie, pour tout entier naturel n,
n2 < (n +1)2wn < n2 +n.
Affirmation 3 : La suite (wn) converge. Vrai.
[n / (n+1)]2 < wn < (n2 +n) /(n+1)2.
La suite définie par [n / (n+1)]2 est croissante et converge vers 1.
La suite (n2 +n) /(n+1)2 est croissante et converge vers 1.
D'après le théorème des gendarmes la suite (wn) converge donc vers 1.
Partie B.
On considère la suite (Un) définie par u0 =0,5 et, pour tout entier naturel n,
Un+1 =2Un / (1+Un).
1. Calculer U1 que l’on écrira sous la forme d’une fraction irréductible.
U1 =2U0 / (1+U0) =1 /1,5 = 2 / 3.
2. Démontrer par récurrence que, pour tout entier naturel n, Un =2n/(1+2n).
Initialisation : U1 = 2 / (1+2), la relation est vraie au rang 1.
Hérédité : la relation est supposée vraie au rang p : Up =2p/(1+2p).
Up+1 =2Up / (1+Up) ; 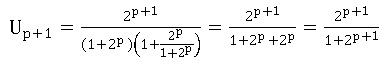
Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est vraie pour tout n entier.
3.
On considère les trois algorithmes suivants dans lesquels les variables
n, p et u sont du type nombre. Pour un seul de ces trois algorithmes la
variable u ne contient pas le terme Un en fin
d’exécution. Déterminer lequel en justifiant votre choix.

Pour n =2.
Algorithme 1
|
Algorithme 2
|
Algorithme 3
|
i
|
i < n
|
u
|
i
|
u
|
p =4
u2=4 /5
|
0
|
vrai
|
u1=2 / 3
|
0
|
u1=2 /3
|
1
|
vrai
|
u2=4 / 5
|
1
|
u2=4 /5
|
2
|
faux
|
|
2
|
u3=8 /9
|
Pour l''algorithme 2 la variable u ne contient pas la valeur de un en fin d'exécution.
.
|
|
|