Mathématiques,
bac S Antilles 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
..
|
|
Exercice 1 : Commun à tous les
candidats (6 points)
Partie A.
Soit 𝑎 et 𝑏 des nombres réels. On considère une fonction 𝑓 définie
sur [0 ; +∞[ par
𝑓(𝑥) =a / (1+e-bx).
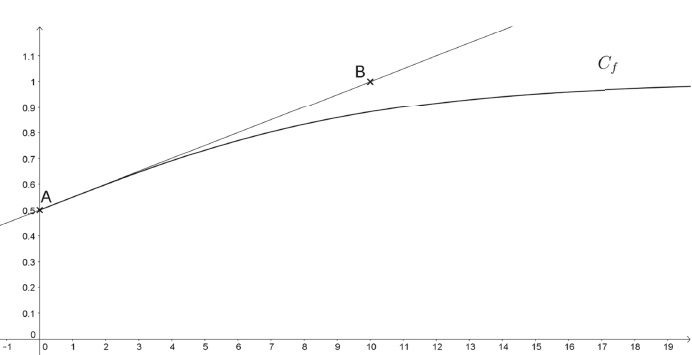
La courbe Cf représentant la fonction 𝑓 dans un repère
orthogonal est donnée ci-dessous.
La courbe Cf passe par le point A(0 ; 0,5).
La tangente à la courbe Cf au point A passe par le point
B(10 ; 1).
1. Justifier que a
= 1.
f(0) = 0,5 = a /(1+e0) = a / (1+1) =0,5 a ; a = 1.
On obtient alors, pour tout réel 𝑥 ≥ 0, f(x) =1 / (1+e-bx).
2. On admet que la
fonction f est dérivable sur [0 ; +∞[ et on note f ' sa fonction
dérivée.
Vérifier que, pour tout réel 𝑥 ≥ 0, f '(x) = be-bx / (1+e-bx)2.
On pose u = 1+e-bx ; u' = -be-bx
; f '(x) = -u' / u2 =
be-bx / (1+e-bx)2.
3. En utilisant
les données de l’énoncé, déterminer b
Equation de la tangente y = c x +d.
c = f '(0) = b / 4 ;
La tangente passe en A(0 ; 0,5) : 0,5 = d.
La tangente passe en B(10 ; 1) : 1 = 2,5b +0,5 ; b = 0,2.
Equation de cette tangente
: y = 0,05 x +0,5.
Partie B.
La proportion d’individus qui possèdent un certain type d’équipement
dans une population est modélisée par la fonction p définie sur [0 ;
+∞[ par p(x) =1 / (1 +e-0,2x)
Le réel x représente le temps écoulé, en année, depuis le 1er
janvier 2000.
Le nombre p(x) modélise la proportion d’individus équipés après x
années.
Ainsi, pour ce modèle, p(0) est la proportion d’individus équipés au 1er
janvier 2000 et p(3,5) est la proportion d’individus équipés au milieu
de l’année 2003.
1. Quelle est, pour
ce modèle, la proportion d’individus équipés au 1er janvier
2010 ? On en donnera une valeur arrondie au centième.
p(10) = 1 / (1 +e-2)=0,88.
2. a. Déterminer le
sens de variation de la fonction p sur [0 ; +∞[.
p '(x) = 0,2e-0,2x / (1+e-0,2x)2.
p'(x) étant strictement positive sur [0
; +∞[ , p(x) est strictement croissante sur cet intervalle.
b. Calculer la limite de la fonction
𝑝 en +∞.
Le terme en exponentielle tend vers zéro si x tend vers plus l'infini.
p(x) tend vers 1 si x tend vers plus l'infini.
c. Interpréter
cette limite dans le contexte de l’exercice.
Au bout d'un temps très long, tous les
individus sont équipés de ce matériel.
3. On considère que, lorsque la
proportion d’individus équipés dépasse 95 %, le marché est saturé.
Déterminer, en expliquant la démarche, l’année au cours de laquelle
cela se produit.
1 / (1 +e-0,2x) > 0,95 ; 1 +e-0,2x < 1 / 0,95 ; e-0,2x < 1 / 0,95 -1 ;
e-0,2x < 0,05 / 0,95 ;
La fonction logarithme étant strictement croissante sur [0
; +∞[.
-0,2x < ln(0,05 /
0,95) ; 0,2 x > ln
(0,95 / 0,05) ;
x > ln (19) / 0,2 ; x >14,7.
Courant 2014, le marché sera saturé.
En 2015, plus de 95 % des individus seront équipés.
4. On définit la proportion moyenne
d’individus équipés entre 2008 et 2010 par :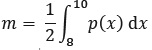
a. Vérifier que,
pour tout réel 𝑥 ≥ 0, p(x) =e0,2x / (1+e0,2x).
p(x) =1 / (1 +e-0,2x)
On multiplie numérateur et dénominateur par e0,2x : Par
suite p(x) =e0,2x / (1+e0,2x).
b. En déduire une
primitive de la fonction p sur [0 ; +∞[.
On pose u = 1 +e0,2x ; u' = 0,2e0,2x ; 5 u'
= e0,2x ; p(x) = 5 u' / u.
Une primitive de la fonction p est p(x) = 5 ln(u) = 5 ln (1+e0,2x).
c. Déterminer la
valeur exacte de 𝑚 et son arrondi au centième.
m = 2,5 [ ln(1+e2) -ln(1+e1,6)] ~0,86.
|
|
|
Exercice
2 : Commun à tous les candidats (5 points)
Les
deux parties de cet exercice sont indépendantes.
Alex et Élisa, deux pilotes de drones, s’entraînent sur un terrain
constitué d’une partie plane qui est bordée par un obstacle.
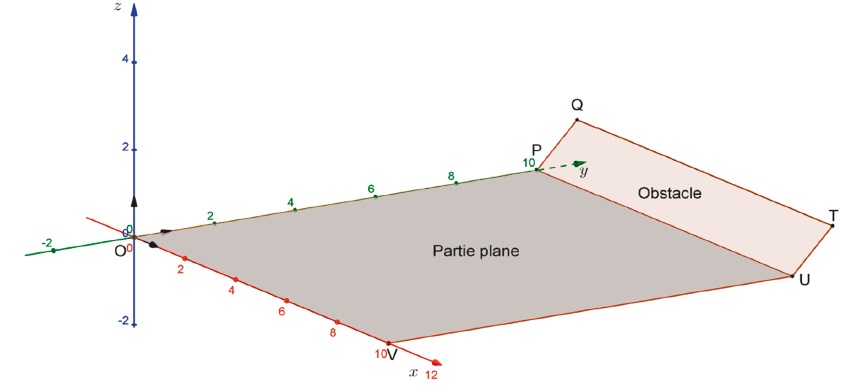
On considère un repère orthonormé , une unité correspondant à dix
mètres. Pour modéliser le relief de la zone, on définit six points O,
P, Q, T, U et V par leurs coordonnées dans ce repère :
O(0 ; 0 ; 0), P(0 ; 10 ; 0), Q(0 ; 11 ; 1), T(10 ; 11 ; 1), U(10 ; 10 ;
0) et V(10 ; 0 ; 0).
La partie plane est délimitée par le rectangle OPUV et l’obstacle par
le rectangle PQTU.
Les deux drones sont assimilables à deux points et on suppose qu’ils
suivent des trajectoires rectilignes :
• le drone d’Alex suit la trajectoire portée par la droite (AB) avec
A(2 ; 4 ; 0,25) et B(2 ; 6 ; 0,75) ;
• le drone d’Élisa suit la trajectoire portée par la droite (CD) avec
C(4 ; 6 ; 0,25) et D(2 ; 6 ; 0,25).
Partie A : Étude de
la trajectoire du drone d’Alex
1. Déterminer une
représentation paramétrique de la droite (AB).
Coordonnées d'un vecteur directeur de cette droite ( 2-2 : 6-4 ;
0,75 -0,25) soit ( 0 ; 2 ; 0,5).
Le point A appartient à cette droite:
x=2 ; y = 2t +4 ; z = 0,5 t +0,25 avec t réel.
2. a. Justifier que le vecteur 𝑛 de coordonnées (0 ; 1 ; −1) est un vecteur normal au plan (PQU).
b. En déduire une équation cartésienne du plan (PQU).

Equation cartésienne de ce plan : y-z+d =0.
Le point P appartient à ce plan : 10 -0 +d = 0 ; d = -10.
y-z-10=0.
3. Démontrer que la droite (AB) et le plan (PQU) sont sécants au point I de coordonnées (2 ; 37 /3 ; 7 /3)
Montrons que I appartient à la droite (AB) :
2t+4 =37 / 3 ; 2t =25/3 ; t = 25 / 6.
De plus 0,5 t +0,25 = 25 /12 +0,25 = 25 / 12 +3 /12 = 28 /12 =7 /3.
Don I appartient bien à la droite (AB).
De plus le vecteur de coordonnées (0 ; 1 ; -1) n'est pas un vecteur
directeur de la droite (AB). Donc la droite (AB) et le plan (PQU) sont
sécant en I.
4. Expliquer pourquoi, en suivant cette trajectoire, le drone d’Alex ne rencontre pas l’obstacle.
La côte du point I ( 37 /3) est supérieure à celle du point U ( 11). Le drone passe au dessus de l'obstacle.
Partie B : Distance minimale entre les deux trajectoires
Pour éviter une collision entre leurs deux appareils, Alex et Élisa
imposent une distance minimale de 4 mètres entre les trajectoires de
leurs drones. L’objectif de cette partie est de vérifier si cette
consigne est respectée.
Pour cela, on considère un point M de la droite (AB) et un point N de la droite (CD).
Il existe alors deux réels a et b tels que 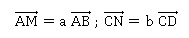
On s’intéresse donc à la distance MN.
1. Démontrer que les coordonnées du vecteur 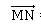 sont (2 − 2b ; 2 − 2a ; −0,5a). sont (2 − 2b ; 2 − 2a ; −0,5a).
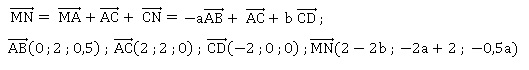
2. On admet que les
droites (AB) et (CD) ne sont pas coplanaires. On admet également que la
distance MN est minimale lorsque la droite (MN) est perpendiculaire à
la fois à la droite (AB) et à la droite (CD).
Démontrer alors que la distance MN est minimale lorsque a = 16 /17 et b = 1.
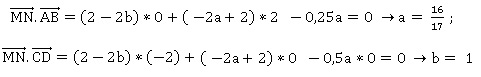
3. En déduire la valeur minimale de la distance MN puis conclure.
MN = [(2-2b)2 +(-2a+2)2 +(-0,5a)2 ]½ = [(2-2)2 +(-32 / 17+2)2 +(-16 / 34)2 ]½ = [(2 /17)2 +(8 /17)2 ]½ ;
MN = [68 / 172] ½=(4 /17)½ =2 /17½~0,49 m.
Or une unité correspond à 10 m ; la distance minimale entre les drones
est 4,9 m, valeur supérieure à 4 m. Les drones ne peuvent pas se
rencontrer.
|
|
|
|
Exercice 3 : Commun à tous les
candidats (4 points)
Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée. Une
réponse non justifiée ne rapporte aucun point. Une absence de réponse
n’est pas pénalisée.
Le plan complexe est muni d’un repère orthonormé direct .
On considère le nombre complexe c=½exp(ip/3) et les points S et T d’affixes respectives c2 et 1 /c.
1. Affirmation 1 : Le nombre c peut s’écrire c = 0,25(1-i 3½). Faux.
c = ½ cos (p/3) +½ i sin (p/3) =0,5( 0,5 + 3½ /2 i ) =0,25(1+i 3½).
2. Affirmation 2 :
Pour tout entier naturel n, c3n est un nombre réel. Vrai.
c3n =0,53n exp(i n p).
3. Affirmation 3 :
Les points O, S et T sont alignés. Vrai.
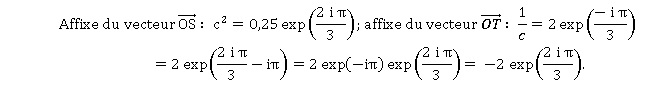
Ces deux vecteurs étant colinéaires, les points O, S et T sont alignés.
4. Affirmation 4 :
Pour tout entier naturel non nul n, |c| + |c2| + ⋯ + |cn| = 1 − 0,5n. Vrai.
|c| = 0,5 ;
Somme des n premiers termes d'une suite géométrique de raison 0,5 et de premier terme 0,5 : |c| + |c2| + ⋯ + |cn| =0,5(1-0,5n) / (1-0,5) ;
|c| + |c2| + ⋯ + |cn| =1 − 0,5n.
Exercice 4. (5 points).
Les trois parties de cet exercice sont indépendantes.
Partie A.
Lors d’une soirée, une chaîne de télévision a retransmis un match.
Cette chaîne a ensuite proposé une émission d’analyse de ce match.
On dispose des informations suivantes :
• 56 % des téléspectateurs ont regardé le match ;
• un quart des téléspectateurs ayant regardé le match ont aussi regardé l’émission ;
• 16,2 % des téléspectateurs ont regardé l’émission.
On interroge au hasard un téléspectateur. On note les événements :
• M : « le téléspectateur a regardé le match » ;
• E : « le téléspectateur a regardé l’émission ».
On note x la probabilité qu’un téléspectateur ait regardé l’émission sachant qu’il n’a pas regardé le match.
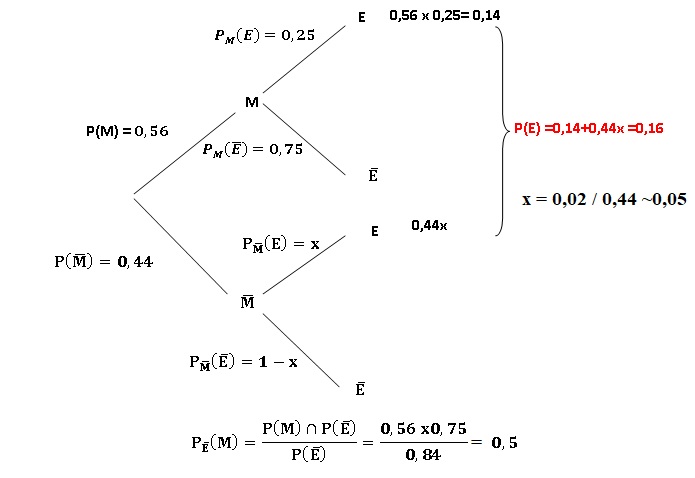
1. Construire un arbre pondéré illustrant la situation.
2. Déterminer la probabilité de 𝑀 ∩ 𝐸.
3. a. Vérifier que 𝑃(𝐸) = 0,44𝑥 + 0,14.
b. En déduire la valeur de 𝑥.
4. Le téléspectateur interrogé n’a pas regardé l’émission. Quelle est la probabilité, arrondie à 10-2, qu’il ait regardé le match ?
|
|
Partie B.
Pour déterminer l’audience des chaînes de télévision, un institut de
sondage recueille, au moyen de boîtiers individuels, des informations
auprès de milliers de
foyers français. Cet institut décide de modéliser le temps passé, en
heure, par un téléspectateur devant la télévision le soir du match, par
une variable aléatoire 𝑇 suivant la loi
normale d’espérance 𝜇 = 1,5 et d’écart-type 𝜎 = 0,5.
1. Quelle est la probabilité, arrondie à 10-3, qu’un téléspectateur ait passé entre une heure et deux heures devant sa télévision le soir du match ?
P(T < 1) =0,15866 ; P(T < 2) =0,84134 ; P(1 < T < 2) =0,84134 -0,15866 ~0,683.
2. Déterminer l’arrondi à 10-2 du réel t tel que 𝑃(𝑇 ≥ t) = 0,066. Interpréter le résultat..
P (T < t) = 1-0,066 = 0,934.
La calculatrice donne t = 2,25.
6,6 % des téléspectateurs ont passé plus de 2 h 15 min devant la télévision le soir du match.
Partie C.
La durée de vie d’un boîtier individuel, exprimée en année, est
modélisée par une variable aléatoire notée S qui suit une loi
exponentielle de paramètre 𝜆 strictement
positif. On rappelle que la densité de probabilité de 𝑆 est la fonction 𝑓 définie sur [0; +∞[ par
f(x) = l exp(-lx).
L’institut de sondage a constaté qu’un quart des boîtiers a une durée de vie comprise entre un et deux ans.
L’usine qui fabrique les boîtiers affirme que leur durée de vie moyenne est supérieure à trois ans.
L’affirmation de l’usine est-elle correcte ? La réponse devra être justifiée.
P(1 < S <2) = e-l -e-2l = 0,25.
On pose X = e-l ;
X-X2-0,25 =0 soit (X-0,5)2 = 0 ; X = 0,5.
e-l = 0,5 ; l = -ln(0,5) = ln(2)
Espérance E = 1 /l = 1 /ln(2) ~1,44.
Cette valeur étant inférieure à 3 ans, l'affirmation de l'usine est fausse.
|
|