Les
océans sous haute surveillance,
bac S ASie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
..
|
|
1. Principe de l’altimétrie radar par satellite.
Un radar embarqué sur le satellite émet verticalement des ondes radio
sous forme de brèves impulsions. On mesure alors le temps de retour de
l’onde émise par le satellite après réflexion sur la surface de la mer.
L'écho de chaque impulsion est détecté et analysé à bord du satellite,
ce qui conduit à une détermination précise de la distance «
altimétrique », c'est-à-dire la distance Ha entre le satellite et le niveau de la mer.
1.1. Donner
l’expression de la durée Δt d’un aller-retour du signal radar en
fonction de la célérité c supposée constante des ondes envoyées par
l’altimètre et de la distance Ha.
2 Ha = c Dt.
1.2. Les ondes
émises et reçues par l’altimètre traversent un milieu qui n’est pas
vide : certaines entités (atomes, molécules, ions...) présentes dans
l’atmosphère peuvent ralentir la propagation des ondes et affecter les
mesures. C’est le cas des électrons,
très abondants vers 400 km d’altitude, de l’air sec et de la vapeur
d’eau à plus basse altitude. Sur Jason, c’est le radiomètre AMR qui
permet, à l’aide de mesures effectuées à trois fréquences, de connaître
le délai induit par l’eau atmosphérique
dans la propagation de l’onde radar de l’altimètre.
Soit Δt1 la durée nécessaire à une onde radar de l’altimètre
pour effectuer un aller-retour dans un nuage de type cumulonimbus de
hauteur h = 2,0 km et d’indice moyen pour l’onde électromagnétique
utilisée n1 = 1,00032.
Soit Δt2 la durée nécessaire à la même onde pour effectuer
un aller-retour dans une colonne atmosphérique, dépourvue de nuage, de
même hauteur h et d’indice moyen n2 = 1,00029.
Les valeurs des indices n1 et n2 ont été obtenues à l’aide du radiomètre.
Données.
L’indice d’un milieu transparent est défini par la relation n = c / v, avec :
- c : célérité des ondes électromagnétiques dans le vide, c = 3,0.108 m.s-1;
- v : célérité des ondes électromagnétiques radio dans le milieu d’indice n.
1.2.a. Montrer que le délai supplémentaire τ = Δt1 – Δt2 induit par la traversée (aller et retour) d’un nuage vaut
𝜏 =2 ℎ /𝑐 (𝑛1 − 𝑛2). Calculer τ.
Δt2 = 2h n2 / c ; Δt1 = 2h n1 / c ;
Δt1 -Δt2 = 2 h / c (𝑛1 − 𝑛2).
t =2 x2 103 /(3 108) (1,00032 -1,00029) =4 10-10 s.
1.2.b.
Calculer la distance d en cm que l’onde électromagnétique radio
parcourrait dans l’atmosphère dépourvue de nuage pendant cette même
durée τ.
4 10-10 x 3 108 =0,12 m = 12 cm.
Conclure sur l’intérêt de l’utilisation du radiomètre.
Le radiomètre mesure la quantité d'eau dans la troposphère ( vapeur d'eau, nuages ) afin d'en déduire la correction à apporter, la précision sur Ha devant être inférieure à 5 cm..
2. Caractéristiques de l’orbite de Jason.
« L'orbite du satellite Jason est choisie de façon à optimiser la
répétition des mesures sur la plus grande partie possible de la surface
du globe. L'altitude de 1336 km est assez élevée pour que le satellite
ne soit plus sensible aux frottements dus au gaz atmosphérique
résiduel, ni aux fluctuations de la gravité liées aux reliefs
terrestres. La stabilité de l'orbite permet de situer avec précision la
position du satellite, sa hauteur Hs et sa trace au sol en longitude et
latitude. »
D’après « Les satellites Jason et la mesure du niveau des océans » Partenariat Eduscol- ENS Lyon.
2.1. Représenter,
sans souci d’échelle, la force, modélisant l'interaction
gravitationnelle exercée par la Terre sur le satellite supposé ponctuel
et noté S (la répartition de masse de la Terre est supposée à symétrie
sphérique).
2.2. Donner
l'expression vectorielle de cette force en fonction de certaines
données de l’énoncé et du vecteur unitaire indiqué sur la figure.
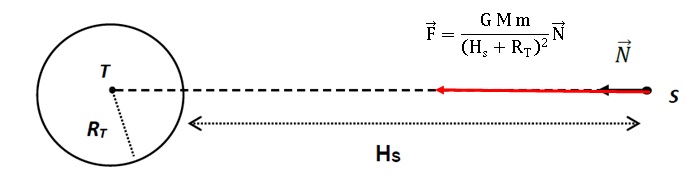
Données
- Terre Masse : M = 5,98 ×1024 kg ; rayon : RT = 6,38×103 km
Période de rotation sur elle-même : TT = 23h 56min 4s
- Jason Masse : m = 510 kg ; altitude : Hs
Période de rotation autour de la Terre : TJ = 112 min
- Constante gravitationnelle : G = 6,67×10-11 N.m2 .kg-2.
2.3. En considérant
la seule action de la Terre, établir l'expression vectorielle de
l'accélération 𝑎⃗ du satellite dans le référentiel géocentrique,
supposé galiléen.
2.4. Montrer que,
dans le cas d'un mouvement circulaire, dont on admettra sans
démonstration qu'il est uniforme, la vitesse V du satellite a pour
expression : V = [GM /(Hs+RT)]½.
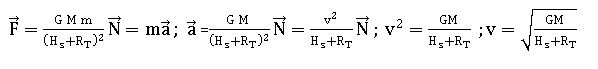
2.5. En déduire la valeur de la période de rotation TS du satellite que l’on comparera à celle donnée dans l’énoncé.
V = [6,67 10-11 x5,98 1024 /(1336 +6,38 103) 103)]½ =7,19 103 m /s.
TS = 2 p(RT+Hs) / V = 2 x3,14 (1336 +6,38 103) 103) /(7,19 103) =6,74 103 s =112,4 min~ 112 min.
Valeur en accord avec celle donnée.
|
|
|
3. Détermination précise de l’orbite
Une détermination très précise de la position du satellite en orbite
est une des conditions essentielles de la qualité des données
altimétriques. Le système DORIS (Détermination d’Orbites et Radio
positionnement Intégré par Satellite), basé sur l'effet Doppler,
contribue en partie à ce délicat exercice d'orbitographie.
Le système DORIS comporte environ 60 stations réparties uniformément
sur tout le globe, chaque station se compose d’une balise émettrice,
d’une antenne réceptrice et d’un jeu de capteurs météorologiques. Les
balises émettent en continu des signaux de différentes fréquences dont
l’une vaut f0 = 401,250 MHz.
3.1. Compléter le document 1 « principe de l’effet Doppler » en faisant l’analogie avec les ondes sonores.
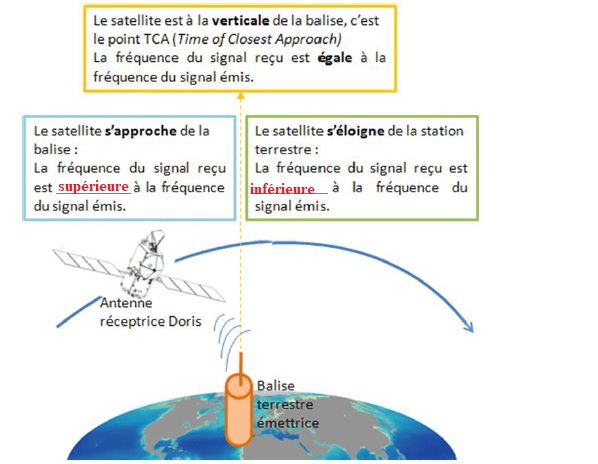
|
|
|
|
3.2. La vitesse v d’un satellite est reliée à la fréquence f0 de l’onde électromagnétique émise par la balise et à la fréquence de l’onde reçue par le satellite fR par la relation
fR = f0 [1 + v cos (q) / c].
avec :
- c, la célérité des ondes électromagnétiques
- q, angle que fait le vecteur vitesse avec la direction balise satellite .
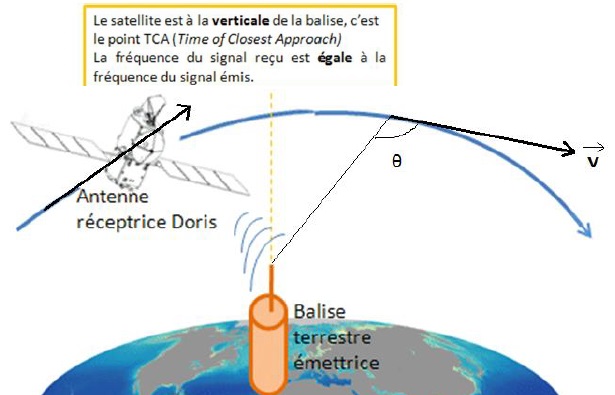
3.2.a. Exprimer la vitesse v du satellite en fonction de la variation de fréquence
Δf = fR-f0 , de f0 , c et cos (𝜃).
fR - f0 = f0 v cos (q) / c ;
Δf c =f0 v cos (q) ; v =
Δf c / (f0 cos (q) ).
3.2.b. Calculer la valeur de la vitesse v du satellite en km.s-1 pour une variation de fréquence Δ𝑓 = - 4,07 kHz et un angle θ = 115°.
Comparer cette valeur à celle que l’on peut calculer à l’aide de l’expression trouvée à la question 2.4.
v = -4,07 103 x3,00 108 / (401,250 106 cos 115) = 7200 m /s = 7,20 km / s.
Cette valeur est en accord avec la vitesse trouvée à la question 2.4 ( 7,19 103 m /s.)
|
|
|