Le
byssus de la moule,
bac S ASie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
| .
. |
|
Les moules sont des mollusques qui ont la faculté de s’accrocher à toutes sortes de supports : rochers, cordes,
coques de bateau. Une glande sécrète le byssus, une colle très
puissante qui durcit sous forme de filaments élastiques résistant à
l’eau, aux rayonnements ultraviolets et au sel.
Cet exercice étudie quelques propriétés remarquables de ces filaments.
La recherche de nouveaux adhésifs efficaces en milieu aqueux a conduit
à isoler les deux principales protéines responsables de l’adhésion du
byssus : la Mfp-3 et la Mfp-5 (Mfp pour Mussel foot protein) contenant
de la L-3,4-dihydroxyphénylalanine, un acide aminé rare plus
communément appelé L-DOPA.
1. Propriétés adhésives.
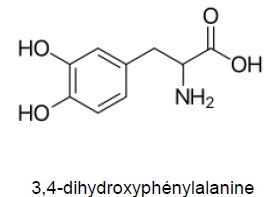
1.1. L'introduction
indique que le byssus contient un acide aminé rare, la 3,4-
dihydroxyphénylalanine. Justifier que cette molécule est bien un acide
aminé.
La molécule possède un groupe amine NH2 et un groupe carboxyle COOH portés par le même carbone.
Dans la suite de l’exercice, on simplifiera la formule de la 3,4-dihydroxyphénylalanine.

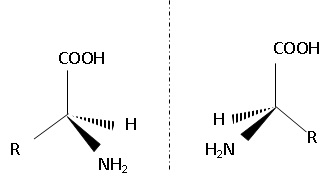
1.2. La L-DOPA est un des deux énantiomères de la 3,4-dihydroxyphénylalanine.
Représenter ces deux énantiomères.
2. Synthèse des protéines des filaments du byssus.
La synthèse en laboratoire des protéines Mfp-3 et Mfp-5 est étudiée à
l’Université de l’lllinois, notamment pour l’élaboration d’adhésifs à
usage médical. Pour obtenir un rendement convenable, on réalise une
synthèse dite convergente, c’est-à-dire la création de petits
polypeptides qui sont ensuite assemblés pour former la protéine finale.
On étudie ici la création d’un dipeptide obtenu à partir de deux
molécules de L-3,4-dihydroxyphénylalanine. Des étapes de la synthèse
sont présentées ci-dessous.
La première étape consiste à protéger le groupe amino de l’acide aminé
par addition d’un groupe 1,1-diméthyléthoxycarbonyle (CH3)3COOC-, noté
Boc en abrégé.
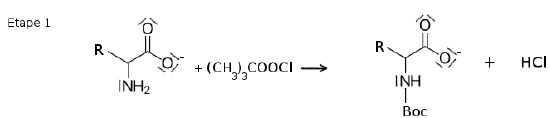
2.1. Justifier la nécessité de cette première étape pour la suite de la synthèse.
A partir de deux acides aminés, sans protection de l'une des fonction
amine ou acide carboxylique, on peut obtenir 4 dipeptides différents.
Si on veut obtenir un seul dipeptide, il faut protéger l'une des
fonctions.
|
|
|
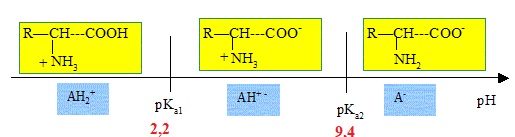
Dans
la L-3,4-dihydroxyphénylalanine, le groupe carboxyle est un acide
faible dont le pKa est proche de 2,2 alors que le groupe amino est une
base faible caractérisée par un pKa proche de 9,4.
2.2. Montrer à l’aide d’un diagramme de prédominance que le pH doit être supérieur à 9,4 pour l’étape 1.
La fonction amine doit être sous la forme NH2.
2.3. Compléter l’étape 4 en faisant apparaître les flèches courbes du mécanisme réactionnel.
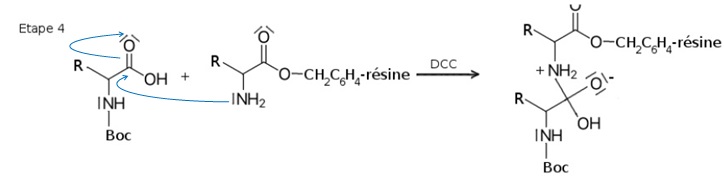
2.4. À quelle catégorie de réactions correspondent respectivement l’étape 4 et l’étape 5 du mécanisme ? Justifier.
L'étape 4 est une addition sur la double liaison C=O du groupe carbonyle.
Une liaison simple est formée, une liaison double disparaît. A partir de deux réactifs, on obtient un seul produit.
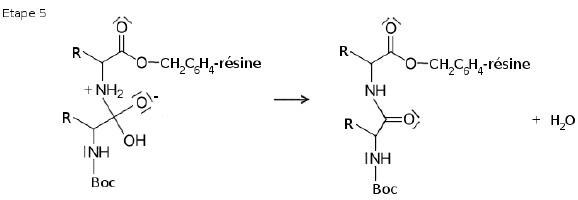
L'étape 5 est l'élimination d'une molécule d'eau. La double liaison C=O est reconstituée.
2.5. En une phrase,
préciser quelle serait l’étape suivante qui permettrait la croissance
de la chaîne peptidique par l’ajout d’un troisième acide aminé.
La fonction ester COO- CH2 C6H4-résine doit être hydrolysée en milieu basique afin de retrouver l'ion carboxylate COO-.
|
|
........
|
|
3. Extraction des protéines des filaments du byssus.
Données Masse volumique du byssus : ρ = 640 kg.m-3.
Pourcentage massique du byssus en Mfp-3 et Mfp-5 : 0,9 %
Pour s’arrimer, une moule forme un réseau d’une cinquantaine de
filaments de byssus qui mesurent entre 4 et 6 cm de long. Pour
déterminer leur diamètre, on procède à des expériences de diffraction
avec trois fils étalons et un filament de byssus que l’on peut
assimiler à un cylindre.
Montage expérimental de diffraction. La longueur d’onde du laser est λ = 630 nm.
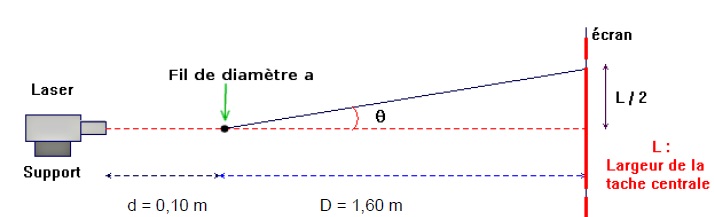
On rappelle que l'écart angulaire θ du faisceau peut être relié à la
longueur d’onde λ (en m) de la lumière monochromatique et au diamètre a
(en m) du fil par l’équation : q = l / a.
Fil étalon
|
F1
|
F2
|
F3
|
Diamètre du fil ( µm)
|
60
|
90
|
120
|
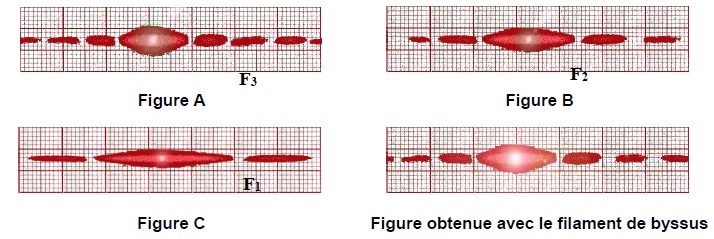
3.1. Associer chacune des figures A, B et C à l’un des fils F1, F2 et F3. Justifier.
La largeur de la tache centrale de diffraction est d'autant plus grande que le diamètre du fil est plus petit.
3.2. On souhaite déterminer la valeur du diamètre a du filament de byssus.
3.2.a. Établir la
relation entre l'écart angulaire θ et la largeur L de la tache centrale
de diffraction. On se placera dans le cas où l’on peut faire
l’approximation tan θ ≈ θ pour un angle θ petit.
D'une part q = l / a et d'autre part tan q ~q = L /(2D) ; l / a =L /(2D) ; L =2 l D / a.
3.2.b. Montrer par un calcul que le diamètre a vaut environ 100 μm.

L a = constante ; 60 x3,2 = 1,8 L ; a ~107 µm.
3.3. À l’université
de Pohang en Corée du Sud, les recherches visent à obtenir les
protéines adhésives Mfp-3 et Mfp-5 en les extrayant à partir de
véritables filaments de byssus.
3.3.a. En prenant
une longueur moyenne de 5 cm pour les filaments du byssus, déterminer
la masse de protéine adhésive extraite à partir d’une seule moule.
Volume de ce cylindre de diamèdre d et de longueur L : pd2 /4 L =3,14 x(100 10-6)2 /4 x0,05 = 3,9 10-10 m3.
Masse correspondante : 640 x 3,9 10-10 =2,5 10-7 kg = 2,5 10-4 g pour un filament.
2,5 10-4 x 50 =1,26 10-2 g pour une moule.
Masse de protéines : 1,26 10-2 x0,9 /100 = 1,13 10-4 g pour une moule.
3.3.b. Estimer le
nombre de moules qu’il faut traiter pour obtenir 1 gramme de protéines
adhésives extraites des filaments de byssus. Conclure sur la pertinence
d’une exploitation des ressources naturelles.
1 /(1,13 10-4) =8,8 103 moules.
Les ressources naturelles seront rapidement épuisées.
|
|
....
..
|
4. Propriétés élastiques des filaments de byssus
Les propriétés adhésives du byssus ne suffisent pas à expliquer la
résistance de l’ancrage des moules, surtout en période de tempête
hivernale.
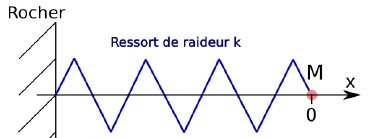
Pour étudier le comportement dynamique de la moule soumise aux vagues,
on assimile celle-ci à un point matériel M et le réseau de filaments de
byssus à un ressort de raideur
k = 500 N.m-1. Initialement, la moule est à l’abscisse x = 0 et, à t = 0, la vague lui communique une vitesse initiale v0 = 2 m.s-1 dirigée suivant l’axe x.
Données
Masse d’une moule : m = 20 g
Force maximale avant rupture du réseau de filaments de byssus : Fmax = 5,1 N
L’intensité de la force de rappel d’un ressort d’axe (O,x) est F = k.x et l’énergie potentielle élastique Epe du ressort est donnée par la relation Epe = ½kx2.
Dans cette partie, on néglige les variations d’énergie potentielle de
pesanteur et, dans un premier temps, on considère que l’énergie
mécanique se conserve durant le mouvement.
Les évolutions temporelles des énergies sont représentées sur le graphique ci-après :
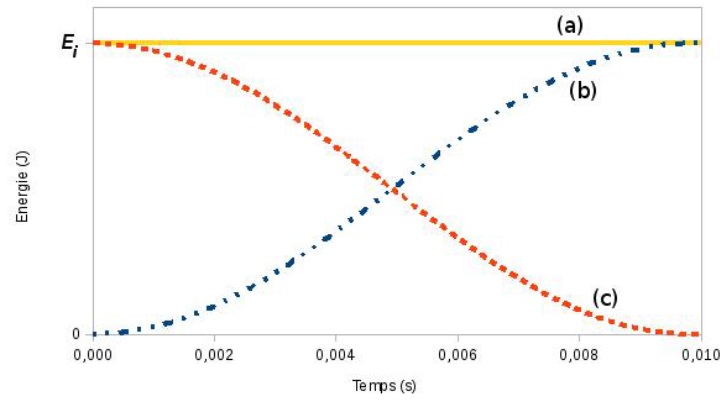
4.1. Identifier parmi les courbes (a), (b) et (c) celle qui correspond à l’énergie cinétique Ec, à l’énergie potentielle élastique Epe et à l’énergie mécanique Em. Justifier brièvement.
Courbe (c) : l'énergie cinétique n'est pas nulle au départ puis décroît.
Courbe (b) : l'énergie potentielle élastique est initialement nulle puis croissante.
Courbe (a) : l'énergie mécanique est la somme des énergies cinétique et potentielle.
4.2. Calculer la valeur de l’énergie mécanique initiale que l’on note Ei.
L'énergie mécanique initiale est sous fgorme cinétique : ½mv02 = 0,5 x 20 10-3 x2,02 = 0,040 J.
4.3. Montrer que l’allongement maximal xmax (à t = 0,010 s) des filaments de byssus est de l’ordre de 1,3 cm.
L'énergie mécanique se trouve sous forme potentielle ; l'énergie mécanique est de plus constante.
0,040 = ½kx2max ; x2max = 0,080 / 500 =1,6 10-4 ; xmax ~1,3 10-2 m = 1,3 cm.
4.4. En déduire la valeur maximale de la force de rappel F que le réseau de filaments de byssus devrait exercer et conclure.
F = k xmax = 500 x1,26 10-2 =6,3 N.
Cette valeur étant supérieure à 5,1 N, il y a rupture des filaments.
En réalité, les filaments jouent aussi un rôle d’amortisseur et dissipent de l’énergie.
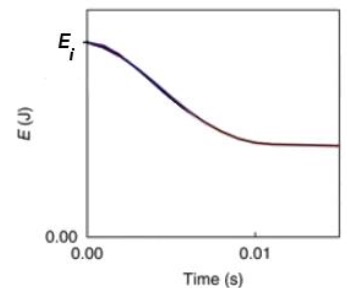
Évolution temporelle de l’énergie mécanique en situation réelle. D’après Qin et Buehler, Nature Communications, Vol 4, 2013.
4.5. Montrer que la
dissipation d’énergie par le réseau de filaments de byssus permet à la
moule de rester accrochée à son support malgré la tempête.
Le réseau de filaments dissipe à peu près la moitié de l'énergie mécanique.
0,020 = ½kx2max ; x2max = 0,040 / 500 =8 10-5 ; xmax ~9,0 10-3 m = 0,90 cm.
F = k xmax = 500 x9 10-3 ~4,5 N.
Cette valeur étant inférieure à 5,1 N, la moule reste accrochée au rocher.
|
|