Mathématiques, bac S Nlle Calédonie 2019

Mathématiques, bac S Nlle Calédonie 2019.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

......

.....

Exercice 1. 5 points.
Une entreprise est spécialisée dans la vente de carrelage.
Les parties A, B et C sont indépendantes.
Partie A.
On suppose dans cette partie que l’entreprise vend des lots de carrelage contenant 25% de carreaux avec motif et 75% de carreaux blancs. Lors d’un contrôle qualité on observe que :
• 2,25% des carreaux sont fissurés ;
• 6% des carreaux avec motif sont fissurés.
On prélève au hasard un carreau.
On note M l’évènement « le carreau a un motif » et F l’évènement « le carreau est fissuré ».
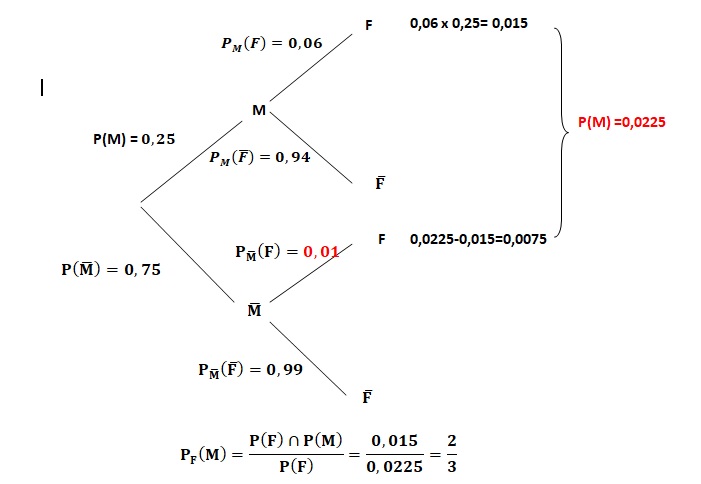
1. Traduire la situation par un arbre pondéré.
2. On sait que le carreau prélevé est fissuré. Démontrer que la probabilité qu’il s’agisse d’un carreau avec motif est 2 /3.
3. Calculer P_M(F), probabilité de F sachant M.

Partie B.
On modélise l’épaisseur en millimètre d’un carreau pris au hasard par une variable aléatoire X qui suit une loi normale d’espérance μ = 11 et d’écart type σ.
Un carreau est commercialisable si son épaisseur mesure entre 10,1 mm et 11,9 mm.
On sait que 99 % des carreaux sont commercialisables.
1. Démontrer que P(X < 10,1) = 0,005.
;
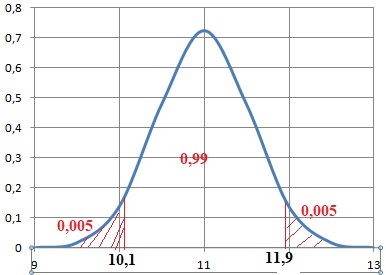P(X > 11,9) = P(X <10,1) =(1-0,99) / 2 = 0,005.
2. On introduit la variable aléatoire Z telle que Z =(X −11) /σ..
a. Donner la loi suivie par la variable aléatoire Z.
Z suit la loi normale centrée réduite.N(0 ; 1).
b. Démontrer que P(Z < -0,9 / s) =0,005.
c. En déduire la valeur de σ arrondie au centième.
P(10,1 < X < 11,9) = 0,99 ; P(10,1-11 < X-11 < 11,9-11) = 0,99 ; P(-0,9 < X-11 < 0,9) = 0,99 ; P(-0,9/ s < (X-11) / s < 0,9 / s) = 0,99 ;
P(-0,9/ s < (Z < 0,9 / s) = 0,99 ; 2P(Z < 0,9 / s)-1 = 0,99 ; P(Z < 0,9 / s) =0,995 ;
P(Z < -0,9 / s) =1-0,995 =0,005
s = 0,35.

Partie C.
On considère la fonction f définie sur [0 ; 2π] par
f (x) = −1,5cos(x)+1,5
On admet que la fonction f est continue sur [0 ; 2π].
On note C₁ la courbe représentative de la fonction f dans un repère orthonormé.

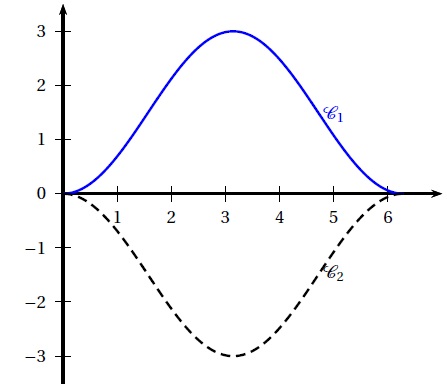
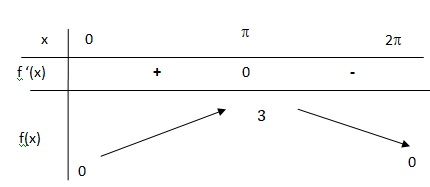
1. Démontrer que la fonction f est positive sur [0 ; 2π].
f(0) = f(2p) =0 et f '(x) = 1,5 sin (x).

2. Sur la figure ci-dessus, la courbe tracée en tiretés, notée C₂, est la courbe symétrique de C₁par rapport à l’axe des abscisses.
La forme d’un carreau est celle de la zone délimitée par les courbes C₁ et C₂.
On note A son aire, exprimée en unité d’aire. Calculer A..

...

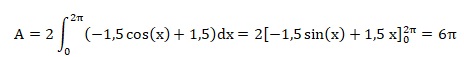
Exercice 2. 5 points.
On considère la fonction f définie sur [0 ; +∞[ par
f (x) = ln((3x +1) / (x +1)).
On admet que la fonction f est dérivable sur [0 ; +∞[ et on note f ′ sa fonction dérivée.
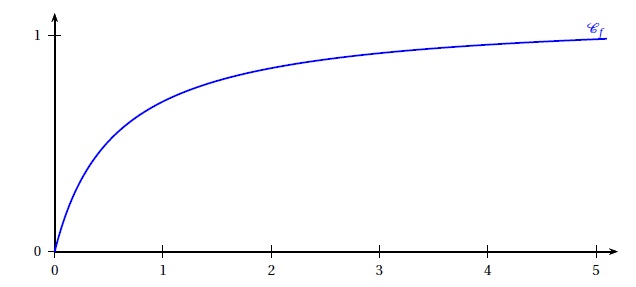
On note C_f la courbe représentative de la fonction f dans un repère orthogonal..

Partie A
1. Déterminer la limite en plus l'infini de f (x) et en donner une interprétation graphique.
x( 3+ 1 /x) / [x(1+1/x)]= (3+1/x) / (1 +1/x).
Quand x tend vers plus l'infini, 1 / x tend vers zéro et (3x +1) / (x +1) tend vers 3.
f(x) tend vers ln(3) quanx tend vers plus l'infini.
La droite d'équation y = ln(3) est asymptote à la courbe C₁.
2. a. Démontrer que, pour tout nombre réel x positif ou nul,
f ′(x) =2 / [(x +1)(3x +1)].
On pose u = 3x+1 et v = x+1 ; u' = 3 ; v' = 1 ; w = u / v.
w '= (u'v-v'u) /v² = [3(x+1)-(3x+1)] /(x+1)² = 2/(x+1)² ;
f '(x) = w ' / w = 2/[(x+1)(3x+1)].
b. En déduire que la fonction f est strictement croissante sur [0 ; +∞[.
Sur cet intervalle la dérivée f '(x) est strictement positive.
La fonction f(x) est donc strictement croissante.

Partie B.
Soit (u_n) la suite définie par u₀ = 3 et, pour tout entier naturel n,u_n+1 = f (u_n) .
1. Démontrer par récurrence que, pour tout entier naturel n,
0,5 < u_n+1 < u_n.
Initialisation : u₁ = f(3) = ln(10 / 4) = ln(2,5).
0,5 < u₁ < u₀est vraie.
Hérédité : la propriété est supposée vraie au rang p.
0,5 < u_p+1 < u_p.
La fonction f(x) étant strictement croissante sur [0 ; +oo[ :
f(0,5) < f(u_p+1) < f(u_p).
f(0,5) < u_p+2 < u_p+1 avec f(0,5) =ln(5 /3) >0,5.
La propriété est vraie au rang p+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout n entier naturel.
2. Démontrer que la suite (u_n) converge vers une limite strictement positive.
f(x) étant positive sur [0 ; +oo[, les termes de la suite sont strictement positifs.
La suite est strictement croissante et bornée. Donc elle converge vers une limite strictement positive.

Partie C.
On note ℓ la limite de la suite (u_n). On admet que f (ℓ) = ℓ.
L’objectif de cette partie est de déterminer une valeur approchée de ℓ.
On introduit pour cela la fonction g définie sur [0 ; +∞[ par g (x)= f (x)−x.
On donne ci-dessous le tableau de variations de la fonction g sur [0 ; +∞[ où
x₀ = (−2+7^½) / 3 ~0,215 et g (x₀) ≈ 0,088, en arrondissant à 10⁻³.

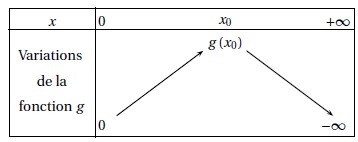
1. Démontrer que l’équation g (x) = 0 admet une unique solution strictement positive. On la note α.
Sur l' intervalle [0 ; x₀ [, g(x)) est continue ( car dérivable) et strictement croissante ; g(0) = 0 ; g(x₀) ~0,088.
Sur l' intervalle [x₀ ; + oo [, g(x)) est continue ( car dérivable) et strictement décroissante ; g(x₀) ~0,088 et g(x) tend vers moins l'infini quand x tend vers plus l'infini.
D'après le théorème de la bijection, l'équation g(x) = 0 admet une unique solution sur cet intervalle.
2.a. Recopier et compléter l’algorithme ci-dessous afin que la dernière valeur prise par la variable x soit une valeur approchée de α par excès à 0,01 près.
b. Donner alors la dernière valeur prise par la variable x lors de l’exécution de l’algorithme.
x ←0,22
Tant que ln((3x +1) / (x +1))-x > 0,01 faire
x ←x +0,01
Fin de Tant que

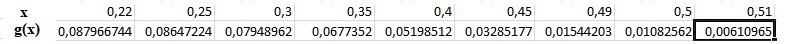
La dernière valeur de x est 0,51.
3. En déduire une valeur approchée à 0,01 près de la limite ℓ de la suite (u_n).
g(0,51) ~0 ; f(0,51) ~0,51.
La limite de la suite est 0,51 à 0,01 près.

....

Exercice 3. 5 points.
Soit ABCDEFGH un cube et I le centre du carré ADHE, c’est-à-dire, le milieu du segment [AH] et du segment [ED]. Soit J un point du segment [CG].
La section du cube ABCDEFGH par le plan (FIJ) est le quadrilatère FKLJ.

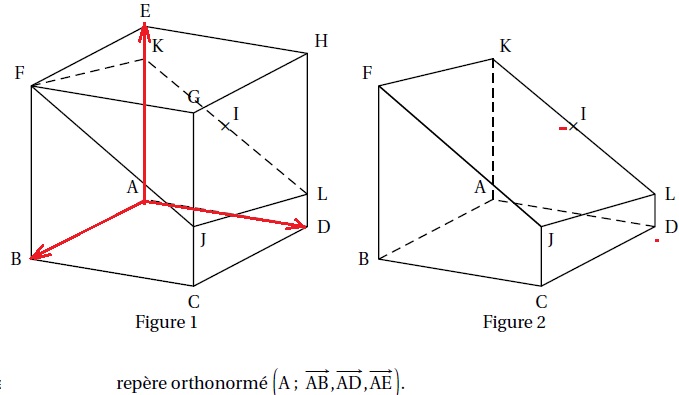
On a donc A(0; 0; 0), B(1; 0; 0), D(0; 1; 0) et E(0; 0; 1).
Les parties A et B peuvent être traitées demanière indépendante.
Partie A.
Dans cette partie, le point J a pour coordonnées (1 ; 1 ; 0,4).
1. Démontrer que les coordonnées du point I sont (0 ; 0,5 ; 0,5).
A(0 ; 0 ; 0) ; H( 0 ; 1 ; 1).
x_I = (x_A +x_H) / 2 = 0 ; y_I = (y_A +y_H) / 2 = 0,5 ; z_I = (z_A +z_H) / 2 = 0,5.
a. Démontrer que le vecteur 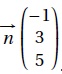est un vecteur normal au plan (FIJ).
F(1 ; 0 ; 1) ; I(0 ; 0,5 ; 0,5) ; J( 1 ; 1 ; 0,4).

b. Démontrer qu’une équation cartésienne du plan (FIJ) est −x +3y +5z −4 = 0.
Equation de ce plan : -x +3y +5z +d = 0.
F appartient à ce plan : -1 +3 *0+5*1+d = 0 ; d = -4.
2. Soit d la droite orthogonale au plan (FIJ) et passant par B.
a. Déterminer une représentation paramétrique de la droite d.
Le vecteur 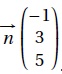est un vecteur directeur de la droite d.
Représentation paramétrique de cette droite :
x = -t+x_B ; y = 3t +y_B ; z = 5 t+z_B avec t réel.
x = -t +1 ; y = 3t ; z = 5 t avec t réel.
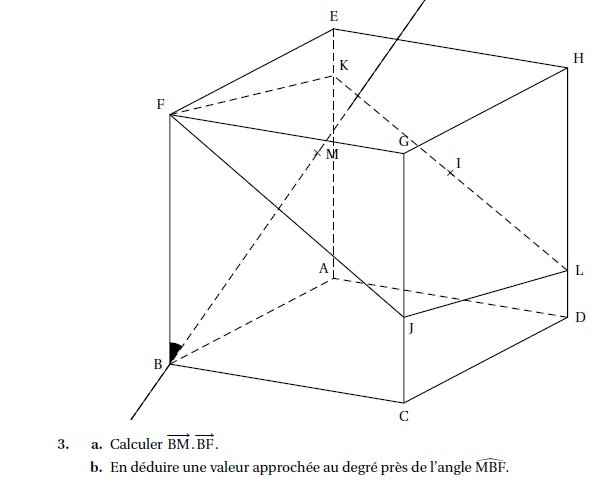
b. On note M le point d’intersection de la droite d et du plan (FIJ).
Démontrer que M ( 6 /7 ; 3 / 7 ; 5 /7).
M appartient à la droite et au plan :
-(-t+1)+3 *3t +5*5t-4 =0 soit 25 t -5=0 ; t = 5 /35 =1 /7.
x_M = -1 / 7+1=6 / 7 ; y_M = 3 / 7 ; z_M =5 / 7.

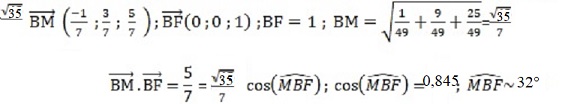
Partie B.
Dans cette partie, J est un point quelconque du segment [CG].
Ses coordonnées sont donc (1 ; 1 ; a), où a est un réel de l’intervalle [0; 1].
1. Montrer que la section du cube par le plan (FIJ) est un parallélogramme.
Les plans (BCF) et (AED) ( faces avant et arrière du cube ) sont parallèles.
L'intersection du plan (BCF) et du plan (FIJ) est la droite (BJ).
L'intersection du plan (AED) et du plan (FIJ) est la droite (KL).
Les droites (KL) et la droite (BJ) sont donc parallèles.
Les plans (ABF) et (CDH) ( faces latérales du cube ) sont parallèles.
L'intersection du plan (ABF) et du plan ( FIJ) est la droite (FK).
L'intersection du plan (CDH) et du plan (FIJ) est la droite (JL).
Les droites (FK) et la droite (JL) sont donc parallèles.
2. On admet alors que L a pour coordonnées (0 ; 1 ; 0,5a).
Pour quelle(s) valeur(s) de a le quadrilatère FKLJ est-il un losange ?
Les côtés consécutifs du parallèlogramme FJLK ont même longueur.
FJ² = 0²+1²+(a-1)² ; JL² = 1²+0²+(0,5a)² ;
(a-1)² +1 = 1 +0,25a² ; (a-1)² = (0,5a)² ;
a-1 = 0,5a ; a = 2 ( exclu).
a-1 = -0,5a ; a = 2 /3.

Exercice 4. 5 points.
Les parties A et B sont indépendantes.
Partie A.
On considère l’équation (E) :
25z² −14z +25 = 0.
1. Résoudre dans C l’équation (E). On écrira les solutions sous forme algébrique.
Discriminant D = (-14)² -4 x25 x25 = -2304 =-(48)².
Solutions : z₁ =(14 +48 i) / 50 =(7 +24 i) / 25 ; z₂ =(7 -24 i) / 25.
2. Démontrer que les solutions de (E) sont de module 1.
|z₁| =|z₂| =[(7² +24²) / 25²]^½=1.
3. On note α le réel de l’intervalle ] 0 ; p/2[ tel que cosα = 7 / 25 et sin a =24 / 25.
Écrire les solutions de (E) sous forme exponentielle en fonction de α.
z₁ = 7 / 25 +24 /25 i = cosα + i sin a ; z₂ = cosα - i sin a ;
z₁ = exp(ia) ; z₂ = exp(-ia) ;
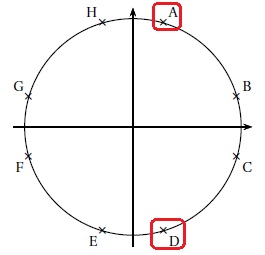
4. La figure ci-dessous fait apparaître huit points du cercle unité. Deux de ces huit points ont une affixe solution de l’équation (E). Lesquels ?

Partie B.
Pour chacune des trois affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée ne rapporte aucun point. Une absence de réponse n’est pas pénalisée.
1. Affirmation A :
(0,5 +i 3^½ /2)²⁰¹⁹ = 1. Faux.
Soit z = 0,5 +i 3^½ /2 ; |z| = (0,5² +3/4)^½ =1.
z = cos(p/3) + i sin (p/3) =exp(ip/3) ; 2019 x p/3 = 673 p = p +672 p.
z²⁰¹⁹ = exp(ip) = -1.

2. Soit z le nombre complexe 1 / 6(2+5i).
Affirmation B :
La limite en plus l'infini de |z|ⁿ est égale à zéro. Vrai.
|z| =(2²+5²)^½ / 6 =29^½ / 6 < 1.
(29^½ / 6)ⁿ tend vers zéro si n tend vers plus l'infini.
3. On rappelle que, pour tout nombre réel x,
cos(2x) = cos²(x)−sin²(x).
Affirmation C :
Pour tout nombre réel a de [−π ; 0] tel que cos(2a) =7 / 25, on a sin(a) = −3 /5. Vrai.
cos (2a) =1-2 sin²(a) = 7 /25.
2 sin²(a) =1-7 /25 = 18 /25.
sin²(a) =9 /25 ; sin(a) = ±3 / 5 ;
sin a= 3 /5 ; a ~37° et a ~180 -37°~143°.
sin(a) = -3 /5 ; a ~-37°et a = 180 +37 ~217°.

menu