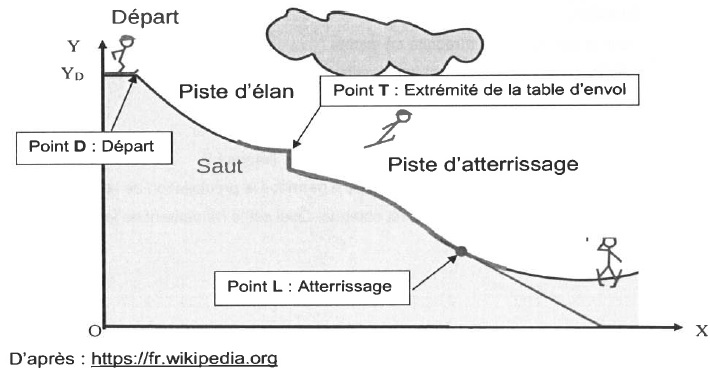
Saut à ski, bac S Liban 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . L'exercice consiste à faire l'étude du skieur sur la piste d'élan et lors du saut dans le cadre d'un modèle simplifié. On donne g = 9,8 m s-2 ; masse du skieir + équipement : m = 70 kg ; altitude de départ yD  = 98 m ; altitude du point d'envol yT = 65 m ; inclinaison de la table d'envol : a = 11° ; vitesse de dcollage vT = 83,3 km / h. Dans le référentiel terrestre, le système [skieur + équipement } sera considéré comme un point matériel. On néglige tout frottement. La vitesse de départ vD est nulle. l'énergie potentielle de pesanteur est nulle en y = 0. 1. Etude du mouvement sur la piste d'élan du tremplin. 1.1. Calculer la valeur de l'énergie mécanique du système en D. La vitesse étant nulle, l'énergie mécanique est sous forme potentielle de pesanteur. EmD = mg yD = 70 x 9,8 x98=6,7228 104 ~6,7 104 J. 1.2. Exprimer l'énergie mécanique en T. EmT = m g yT +½mv2T. 1.3. Montrer que vT = (2g(yD-yT))½ et calculer sa valeur. Conservation de l'énergie mécanique du système : m g yT +½mv2T = mg yD ; g yT +½v2T = g yD ; ½v2T =g(yD-yT) ; vT = (2g(yD-yT)½ = (2 x9,8 (98-65))½ =25,43 ~25 m /s. ( 25,43 x3,6 ~92 km /h) 1.4. Ce résultat est-il en accord avec la vitesse mesurée ? Commenter. La valeur calculer est supérieur d'environ 10 km / h à la valeur mesurée. Dans cette étude on a négligé les frottements. 2. Etude du mouvement lors du saut. On modèlise la piste d'atterrissage par une droite d'équation ypiste = -0,59 x. On note xL l'abscisse de L. 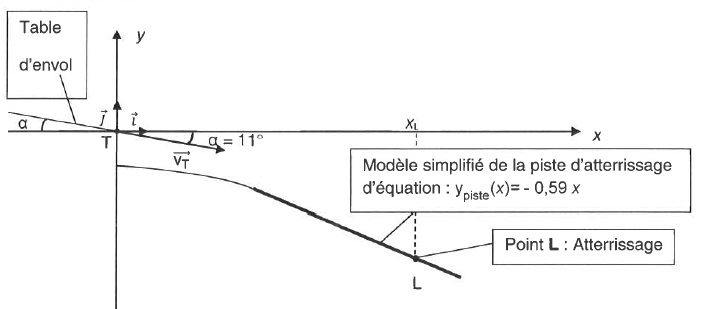2.1. Déterminer les coordonnées du vecteur accélération. Le skieur  n'est soumis qu'à son poids. La seconde loi de Newton conduit à : ax = 0 et ay = -g. 2.2. Montrer que les équations horaires du point matériel M s'écrivent : x = vT cos a t ; y = -½gt2 -vT sin a t. Le vecteur vitesse est une primitive du vecteur accélération. Vitesse initiale en T :  vT cos a  ; -vT sin a ; Vitesse à la date t : vT cos a  ; -vT sin a -gt. Le vacteur position est une primitive du vecteur vitesse et la position initiale est l'origine du repère. x = vT cos a t ; y = -½gt2 -vT sin a t. 2.3. En déduire l'équation de la trajectoire. t = x / (vT cos a) ; repport dans y : y = -½g x2 / (vT cos a)2 - x tan a. 2.4. Le jour de l'épreuve, la longueur réelle du saut a été de 113 m. Cette longueur correspond à TL ( abscisse réelle du point L = 97 m) Le modèle précédent permet-il de rendre compte de la valeur réelle de l'abscisse du point L ? Commenter. TL = (xL2 +yL2)½. yL = -0,59 xL. yL = -½g xL2 / (vT cos a)2 - xL tan a. vT = 83,3 / 3,6 = 23,14 m / s. yL =-4,9 xL2 / (23,14 cos 11)2 - xL tan 11. yL = -9,5 10-3 xL2  - 0,194xL. -0,59 xL = -9,5 10-3 xL2  - 0,194 xL. -9,5 10-3 xL2  + 0,396xL = 0. xL = 0,396 / (9,5 10-3) ~41,7 m. Par suite yL = -0,59 x 41,7 = -24,6 m. TL = (41,72 +(-24,6)2)½~48 m. Le modèle précédent ne permet pas de rendre compte de la longueur réelle. La présence de vent le jour de l'épreuve a permis au skieur de planer beaucoup plus loin.

menu