Mathématiques, bac S Liban 2019.

Mathématiques, bac S Liban 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

...

Exercice 1 : Commun à tous les candidats (5 points)
Le plan est muni d’un repère orthogonal .
1. On considère la fonction f définie sur l’intervalle ]0; 1] par f (x) = x(1−lnx) ² .
a. Déterminer une expression de la fonction dérivée de f et vérifier que pour tout x ∈]0 ; 1], f ′ (x) = (lnx +1)(lnx −1).
On pose u = x et v = (1-ln x)² ; u' = 1 ; v' = - 2(1-ln x) / x .
u'v +v'u = (1-ln x)² -2(1-ln x) =(1-ln x) ( 1-ln x -2) = -(1-ln x)(1+ln x) =(lnx +1)(lnx −1).
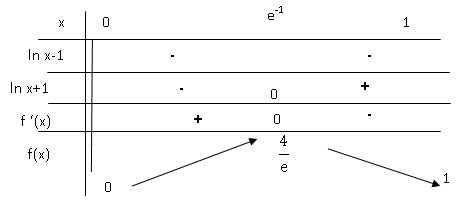
b. Étudier les variations de la fonction f et dresser son tableau de variations sur l’intervalle ]0; 1] (on admettra que la limite de la fonction f en 0 est nulle).
lnx-1 est négatif ;
ln x +1 = 0 ; ln x = -1 ; x = e^-1.

On note Γ la courbe représentative de la fonction g définie sur l’intervalle ]0; 1] par g (x) = lnx. Soit a un réel de l’intervalle ]0; 1]. On note M_a le point de la courbe Γ d’abscisse a et d_a la tangente à la courbe Γ au point M_a . Cette droite da coupe l’axe des abscisses au point N_a et l’axe des ordonnées au point P_a . On s’intéresse à l’aire du triangle ON_aP_a quand le réel a varie dans l’intervalle ]0; 1]. 2. Dans cette question, on étudie le cas particulier où a = 0,2 et on donne la figure ci-dessous.

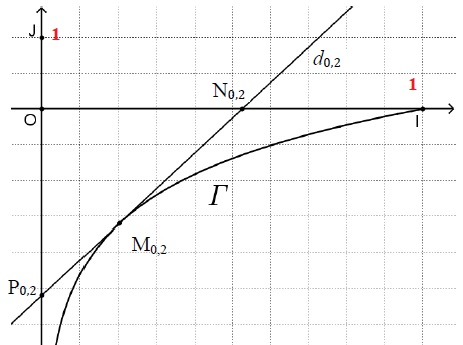
a. Déterminer graphiquement une estimation de l’aire du triangle ON_0,2P_0,2 en unités d’aire.
0,52 x2,6 / 2 = 0,676 unité d'aire.
b. Déterminer une équation de la tangente 𝑑_0,2 .
Coefficient directeur : g'(0,2) = 1 / 0,2 = 5.
La tangente passe par le point M₀₂(0,2 ; ln(0,2) : y = 5 x0,2 +b = ln(0,2) = -ln(5) ; b = -1-ln(5).
y = 5x -1-ln 5.
c. Calculer la valeur exacte de l’aire du triangle O_N0,2P_0,2 .
OP₀₂ =(1+ln 5) ; ON₀₂ =(1+ln 5) / 5 ; Aire = (1+ln 5)² / 10.
Dans ce qui suit, on admet que, pour tout réel 𝑎 de l’intervalle ]0 ;1], l’aire du triangle ON𝑎P𝑎 en unités d’aire est donnée par :
𝐴(𝑎)=0,5𝑎 (1 –ln𝑎)².
3. À l’aide des questions précédentes, déterminer pour quelle valeur de 𝑎 l’aire 𝐴(𝑎) est maximale. Déterminer cette aire maximale.
f(x) passe par un maximum pour x = e^-1.
L'aire est maximale pour x = e^-1 et vaut : 0,5 e^-1 (1+ln e)² = 2 e^-1.

Exercice 2 : Commun à tous les candidats (4 points)
Le plan complexe est muni d’un repère orthonormé direct d’unité 2 cm. On appelle 𝑓 la fonction qui, à tout point M, distinct du point O et d’affixe un nombre complexe 𝑧, associe le point M′ d’affixe 𝑧′ tel que 𝑧′=−1 /𝑧.
1. On considère les points A et B d’affixes respectives 𝑧_A=−1+i et 𝑧_B=0,5exp(ip/3).
a. Déterminer la forme algébrique de l’affixe du point A′ image du point A par la fonction 𝑓.
z'_A = -1 / (-1+i) = (1+i) / 2.
b. Déterminer la forme exponentielle de l’affixe du point B′ image du point B par la fonction 𝑓.
z'_B = -1/ (0,5 exp(ip/3))= -2 exp(-ip/3) = 2 exp( ip) exp(-ip/3) = 2 exp((2ip/3).
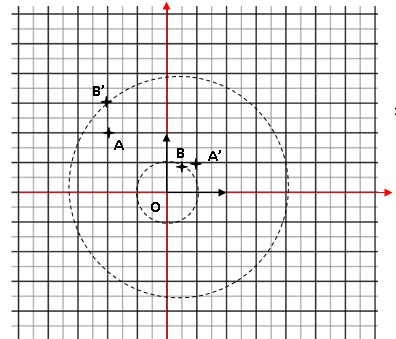
c. Sur la copie, placer les points A, B, A′ et B′ dans le repère orthonormé direct . Pour les points B et B′, on laissera les traits de construction apparents.

2. Soit 𝑟 un réel strictement positif et 𝜃 un réel. On considère le complexe 𝑧 défini par 𝑧=𝑟e^iθ.
a. Montrer que 𝑧′=1/𝑟exp(i(π−θ)).
z' = -1 / (r exp(iq)) = -1 /r e^-iq =1 / r e^ip e^-iq =1/𝑟exp(i(π−θ))
b. Est il vrai que si un point M, distinct de O, appartient au disque de centre O et de rayon 1 sans appartenir au cercle de centre O et de rayon 1, alors son image M′ par la fonction 𝑓 est à l’extérieur de ce disque ? Justifier.
r <1 ; 1 / r > 1 : M' est donc en dehors du disque de centre O et de rayon 1. L'affirmation est vraie.
3. Soit le cercle G de centre K d’affixe 𝑧_K= -0,5 et de rayon 0,5.
a. Montrer qu’une équation cartésienne du cercle est 𝑥²+𝑥+𝑦²=0.
Equation cartésienne du cercle : (x+0,5)² + y² = 0,5² ; x² +x +0,25 + y² =0,25 ; 𝑥²+𝑥+𝑦²=0.
b. Soit 𝑧=𝑥+i𝑦 avec 𝑥 et 𝑦 non tous les deux nuls. Déterminer la forme algébrique de 𝑧′ en fonction de x et y.
z' = -1 / (x+iy) = -(x-iy) / (x²+y²) = (-x+iy) / (x²+y²).
c. Soit M un point, distinct de O, du cercle G . Montrer que l’image M′ du point 𝑀 par la fonction 𝑓 appartient à la droite d’équation 𝑥=1.
M appartient au cercle G : x = -(y²+x²).
z' = 1 -iy / x.
M' appartient à la droite d'équation x = 1.

Exercice 3 : Commun à tous les candidats (6 points)
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Dans un plan 𝑃, on considère un triangle ABC rectangle en A.
Soit 𝑑 la droite orthogonale au plan 𝑃 et passant par le point B. On considère un point D de cette droite distinct du point B.

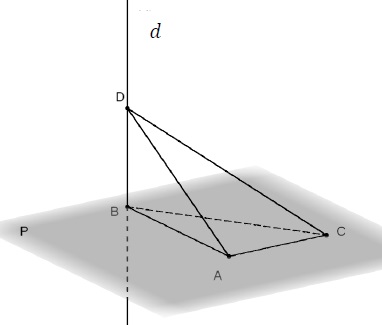
1. Montrer que la droite (AC) est orthogonale au plan (BAD).
La droite (d) est orthogonale au plan (BAC), elle est donc orthogonale à toute droite de ce plan, et en particulier à la droite ( AC).
Le triangle ABC est rectengle en A. La droite ( AC) est perpendiculaire à la droite (AB).
La droite (AC) est perpendiculaire aux deux droites (AB) et (d), droites sécantes.
La droite (AC) est donc orthogonale au plan (BAD).
On appelle bicoin un tétraèdre dont les quatre faces sont des triangles rectangles.
2. Montrer que le tétraèdre ABCD est un bicoin.
La droite (d) étant orthogonale au plan (ABC), les triangles DBA et DBC sont rectangles en B.
De plus le triangle ABC est rectangle en A.

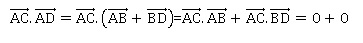
3. a. Justifier que l’arête [CD] est la plus longue arête du bicoin ABCD.
Le triangle ABD étant rectangle en B : AD > AB ; AD > BD.
Le triangle BCD étant rectangle en B : CD > BC ; CD > BD.
Le triangle ABC étant rectangle en A : BC > AB ; BC > AC.
Le triangle ACD étant rectangle en A : CD > AD ; CD > AC.
Donc CD > AD ; CD > BD ; CD > BC ; CD > AB.
b. On note I le milieu de l’arête [CD]. Montrer que le point I est équidistant des 4 sommets du bicoin ABCD.
Le triangle ACD, restangle en A est inscrit dans le demi-cercle de diamètre CD et de centre I. I est donc équidistant des points C, A et D.
Le triangle BCD, restangle en B est inscrit dans le demi-cercle de diamètre CD et de centre I. I est donc équidistant des points C, B et D.
I est donc équidistant des 4 sommets.

Partie B.
Dans un repère orthonormé de l'espace, on considère le point A (3 ;1 ;−5) et la droite 𝑑 de représentation paramétrique
{𝑥=2𝑡+1 ; 𝑦=−2𝑡+9 ; 𝑧=𝑡−3 où 𝑡 appartient à R.
1. Déterminer une équation cartésienne du plan 𝑃 orthogonal à la droite 𝑑 et passant par le point A.
Coordonnées du vecteur directeur de la droite d : ( 2 ; -2 ; 1).
Equation cartésienne du plan P : 2x -2y +z +d = 0.
Le point A appartient à ce plan : 2 *3 -2*1 -5 +d = 0 ; d = 1.
2x -2y +z +1 = 0.
2. Montrer que le point d’intersection du plan 𝑃 et de la droite 𝑑 est le point B(5 ;5 ;−1).
2(2t+1) -2(-2t+9)+t-3 +1 = 0 ;
4t +2 +4t-18 +t-3+1=0 ; 9t = 18 ; t = 2.
x_B =5 ; y_B = 5 ; z_B=-1.
3. Justifier que le point C (7 ;3 ;−9) appartient au plan 𝑃 puis montrer que le triangle ABC est un triangle rectangle isocèle en A.
2x_C -2y_C +z_C+1 = 14-6-9+1=0; C appartient au plan P.

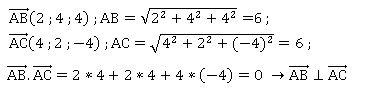
4. Soit t un réel différent de 2 et M le point de paramètre 𝑡 appartenant à la droite 𝑑.
a. Justifier que le triangle ABM est rectangle.
Les points B et M appartiennent à la droite d orthogonale au plan B ; la droite (BM) est donc orthoginale à la droite (AB) du plan P.
b. Montrer que le triangle ABM est isocèle en B si et seulement si le réel 𝑡 vérifie l’équation 𝑡² 4𝑡=0.

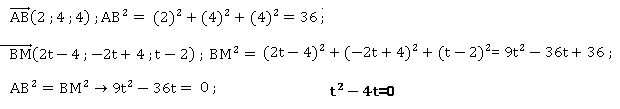
c. En déduire les coordonnées des points M₁ et M₂ de la droite 𝑑 tels que les triangles rectangles ABM₁ et ABM₂ soient isocèles en B.
(t-4) t = 0 soit : t =0 : M₁(1 ; 9 ; -3).
t = 4 : M₂(9 ; 1 ; 1).

Partie C.
On donne le point D(9 ; 1 ; 1) qui est un des deux points solutions de la question 4.c. de la partie B.
Les quatre sommets du tétraèdre ABCD sont situés sur une sphère. En utilisant les résultats des questions des parties A et B précédentes, déterminer les coordonnées du centre de cette sphère et calculer son rayon.
Soit I le milieu de l'arète CD, c'est à dire le centre de la sphère de rayon DI.
CD² = 2²+(-2)²+10²=108 ; CD =6 *3^½ : Rayon de la sphère : 3 *3^½.
x_I = 0,5(x_C +x_D) =8 ; y_I = 0,5(y_C +y_D) =2 ; z_I = 0,5(z_C +z_D) = -4.

Exercice 4. 4 points.

Chaque semaine, un agriculteur propose en vente directe à chacun de ses clients un panier de produits frais qui contient une seule bouteille de jus de fruits. Dans un esprit de développement durable, il fait le choix de bouteilles en verre incassable et demande à ce que chaque semaine, le client rapporte sa bouteille vide.
On suppose que le nombre de clients de l’agriculteur reste constant.
Une étude statistique réalisée donne les résultats suivants :
– à l'issue de la première semaine, la probabilité qu'un client rapporte la bouteille de son panier est 0,9 ;
– si le client a rapporté la bouteille de son panier une semaine, alors la probabilité qu’il ramène la bouteille du panier la semaine suivante est 0,95 ;
– si le client n'a pas rapporté la bouteille de son panier une semaine, alors la probabilité qu’il ramène la bouteille du panier la semaine suivante est 0,2.
On choisit au hasard un client parmi la clientèle de l’agriculteur. Pour tout entier naturel n non nul, on note 𝑅𝑛 l’événement « le client rapporte la bouteille de son panier de la 𝑛 ième semaine ».
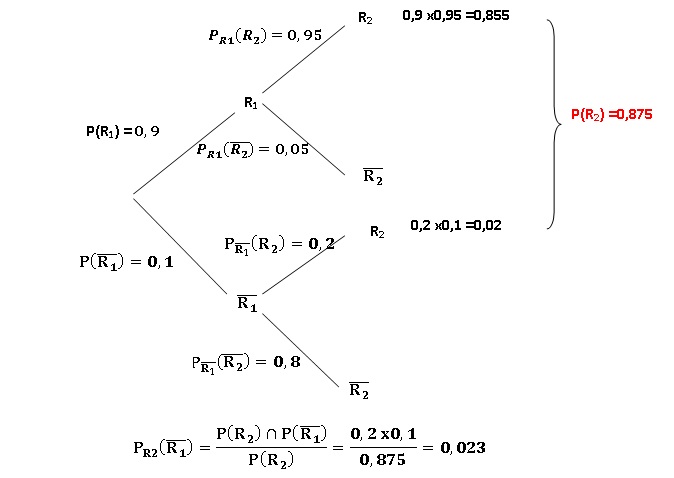
1. a. Modéliser la situation étudiée pour les deux premières semaines à l’aide d’un arbre pondéré qui fera intervenir les événements 𝑅1 et 𝑅2.
b. Déterminer la probabilité que le client rapporte ses bouteilles des paniers de la première et de la deuxième semaine.
c. Montrer que la probabilité que le client rapporte la bouteille du panier de la deuxième semaine est égale à 0,875.
d. Sachant que le client a rapporté la bouteille de son panier de la deuxième semaine, quelle est la probabilité qu'il n’ait pas rapporté la bouteille de son panier de la première semaine ? On arrondira le résultat à 10⁻³.

2. Pour tout entier naturel 𝑛 non nul, on note 𝑟_𝑛 la probabilité que le client rapporte la bouteille du panier de la 𝑛 ième semaine. On a alors 𝑟_𝑛=𝑃(𝑅_𝑛).
a. Recopier et compléter l'arbre pondéré (aucune justification n’est attendue) :

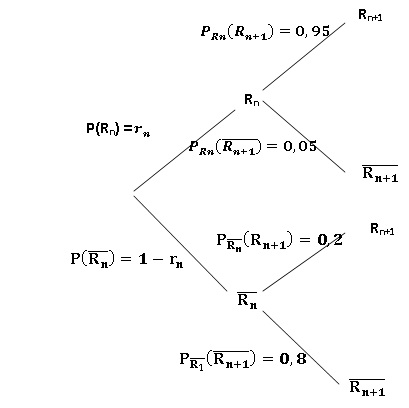
b. Justifier que pour tout entier naturel 𝑛 non nul, 𝑟_𝑛+1=0,75×𝑟_𝑛+0,2.
Formule des probabilités totales : r_n+1 = 0,95 r_n +(1-r_n) x0,2 = 0,75×𝑟_𝑛+0,2.
c. Démontrer que pour tout entier naturel 𝑛 non nul, 𝑟_𝑛=0,1×0,75^𝑛−1+0,8.
Initialisation : r₁ = 0,95 = 0,1 x0,75⁰ +0,8 = 0,1 +0,8 = 0,9, la propriété est vraie au rang 1.
Hérédité : la propriété est supposée vraie au rang p ; 𝑟_p=0,1×0,75^p−1+0,8.
r_p+1= 0,95 r_p +(1-r_p) x0,2 =0,75 r_p +0,2 =0,1 x 0,75^p+0,75 x 0,8 +0,2 = 0,1 x 0,75^p+0,8.
La propriété est vraie au rang p+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle vraie pour tout n.
d. Calculer la limite de la suite (𝑟_𝑛). Interpréter le résultat dans le contexte de l’exercice.
-1 < 0,75 < 1, donc 0,75^p tende vers zéro si p tend vers plus l'infini.
La limite de la suite (r_n) est 0,8.
La probabilité que le client rapporte sa bouteille au bout de plusieurs semaine est égale à 0,8.

menu