Mathématiques,
bac S Métropole 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
..
|
|
Exercice 1 : Commun à tous les
candidats (6 points).
Partie A.
On considère la fonction 𝑓 définie sur l’ensemble 𝐑 des nombres réels par :
𝑓(𝑥) = 3,5-0,5(ex+e-x).
a. Déterminer la limite de la fonction 𝑓 en +∞.
Quand x tend vers plus l'infini : e-x tend vers zéro ; ex tend vers plus l'infini ;
-0,5 ex tend vers moins l'infini ; f(x) tend vers moins l'infini.
b. Montrer que la fonction 𝑓 est strictement décroissante sur l’intervalle [0;+∞[.
Dérivée f '(x) = -0,5(ex-e-x) = 0,5[(1-e2x) / ex]
ex > 0 ; (1-e2x) < 0 ; f '(x) est négative ou nulle.
f(x) est strictement décroissante sur [0;+∞[.
c. Montrer que l’équation 𝑓(𝑥) = 0 admet, sur l’intervalle [0;+∞[, une unique solution, qu’on note 𝛼.
f(0) =2,5 ; f(x) tend vers moins l'infini quand x tend vers plus l'infini.
De plus f(x) est continue et strictement décroissante sur [0;+∞[.
D'après le corollaire du théorème des valeurs intermédiaires, l'équation f(x) = 0 admet une seule solution sur cet intervalle.
2.
En remarquant que, pour tout réel 𝑥, 𝑓(−𝑥) = 𝑓(𝑥), justifier que
l’équation 𝑓(𝑥) = 0 admet exactement deux solutions dans R et
qu’elles sont opposées.
f(a) = f(-a) =0.
Dans l'hypothèse d'une autre solution,notée ß, sur R-, alors f(-ß) = f(
=0 ; cela implique une deuxième solution sur [0 ; +oo[, ce qui est
impossible.
f(x) = 0 admet deux solutions opposées sur R.
Partie B.
Les serres en forme de tunnel sont fréquemment utilisées pour la
culture des plantes fragiles ; elles limitent les effets des
intempéries ou des variations de température.
Elles sont construites à partir de plusieurs arceaux métalliques
identiques qui sont ancrés au sol et supportent une bâche en plastique.
Le plan est rapporté à un repère orthonormé d’unité 1 mètre. La
fonction 𝑓 et le réel 𝛼 sont définis dans la partie A. Dans la suite
de l’exercice, on modélise un arceau de serre par la courbe de la
fonction 𝑓 sur l’intervalle [– 𝛼; 𝛼].
On a représenté ci-dessous la courbe sur l’intervalle [– 𝛼; 𝛼].
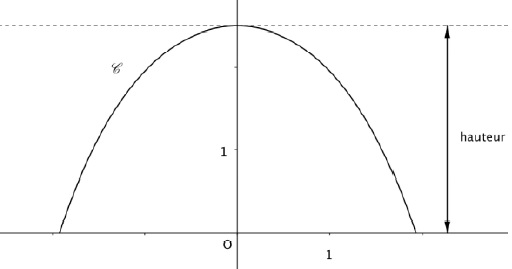
On admettra que la courbe admet l’axe des ordonnées pour axe de symétrie.
1. Calculer la hauteur d’un arceau.
f(0) = 3,5-0,5(e0+e-0) = 3,5-1 = 2,5 m.
2. a. Dans cette
question, on se propose de calculer la valeur exacte de la longueur de
la courbe sur l’intervalle [0; 𝛼]. On admet que cette longueur est
donnée, en mètre, par l’intégrale :
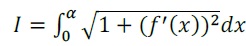
Montrer que pour tout réel x, on a : 1 + (𝑓 '(𝑥))2 = 0,25(ex+e-x)2.
1+0,52[(1-e2x) / ex]2 =[ e2x +0,25(1-e2x)2] / e2x =[ e2x +0,25(1-2e2x+e4x)] / e2x ;
0,25[ 4e2x +1-2e2x+e4x] / e2x =0,25[ 1+2e2x+e4x] / e2x =0,25(1+e2x)2 / e2x =0,25(e-x+ex)2.
b. En déduire la valeur de l’intégrale 𝐼 en fonction de 𝛼.
Justifier que la longueur d’un arceau, en mètre, est égale à : 𝑒a − 𝑒-a.
Primitive de 0,5(e-x+ex) : F = 0,5 (-e-x+ex).
I = F(a) -F(0) =0,5 [ea -e-a].
Longueur de l'arc 2I =𝑒a − 𝑒-a.
Partie C.
On souhaite construire une serre de jardin en forme de tunnel.
On fixe au sol quatre arceaux métalliques, dont la forme est celle
décrite dans la partie précédente, espacés de 1,5 mètre, comme indiqué
sur le schéma ci-dessous.
Sur la façade sud, on prévoit une ouverture modélisée sur le schéma par
le rectangle ABCD de largeur 1 mètre et de longueur 2 mètres.
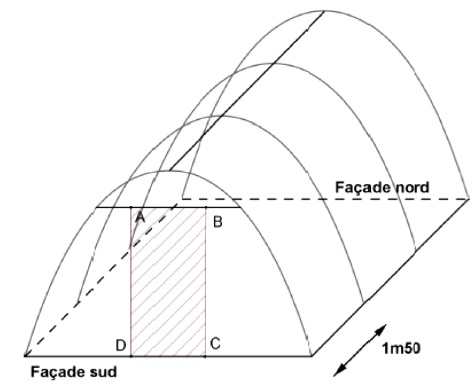
On souhaite connaître la quantité, exprimée en m², de bâche plastique nécessaire pour réaliser cette serre.
Cette bâche est constituée de trois parties, l’une recouvrant la façade nord, l’autre la façade sud (sauf
l’ouverture), la troisième partie de forme rectangulaire recouvrant le dessus de la serre.
1. Montrer que la quantité de bâche nécessaire pour recouvrir les façades sud et nord est donnée, en m2, par :
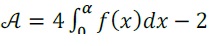
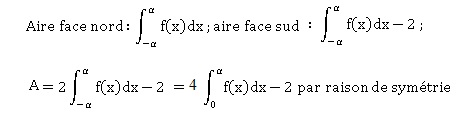
2. On prend 1,92 pour valeur approchée de 𝛼. Déterminer, au m2 près, l’aire totale de la bâche plastique nécessaire pour réaliser cette serre.
Aire de la couverture : (e1,92-e-1,92) x4,5 =(6,82 -0,147) x4,5 ~30 m2.
Primitive de f(x) : F(x) =3,5x -0,5(ex-e-x).
Aire des deux faces : 4 (3,5 x1,92 -0,5(e1,92 -e-1,92) -2=4(6,72 -0,5(6,82 -0,147) -2 = 11,5 m2.
Total : 11,5 +30 ~ 42 m2.
|
|
|
Exercice
2 : Commun à tous les candidats (5 points)
Une plateforme informatique propose deux types de jeux vidéo : un jeu de type A et un jeu de type B.
Partie A.
Les durées des parties de type A et de type B, exprimées en minutes,
peuvent être modélisées respectivement par deux variables aléatoires
notées 𝑋G et 𝑋H.
La variable aléatoire 𝑋G suit la loi uniforme sur l’intervalle [9; 25] .
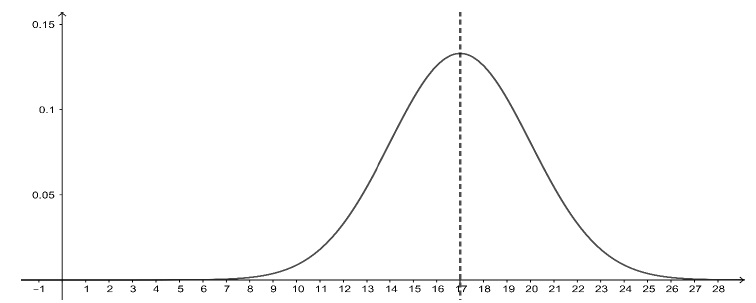
La variable aléatoire 𝑋H suit la loi normale de moyenne 𝜇
et d’écart type 3. La représentation graphique de la fonction de
densité de cette loi normale et son axe de symétrie sont donnés
ci-dessous.
1.a. Calculer la durée moyenne d’une partie de type A.
E(XA) = (9 +25) / 2 = 17 minutes.
b. Préciser à l’aide du graphique la durée moyenne d’une partie de type B.
L'axe de symétrie se situe à µ = 17 minutes.
2. On choisit au
hasard, de manière équiprobable, un type de jeu. Quelle est la
probabilité que la durée d’une partie soit inférieure à 20 minutes ? On
donnera le résultat arrondi au centième.
P(XA < 20) =(20-9) /(25-9) =11 / 16 =0,6875~0,69
P(XB < 20) =0,8413~0,84.
Le choix du jeu étant équiprobable, la probabilité demandée est : (0,6875 +0,8413 ) / 2 ~0,76.
Partie B.
On admet que, dès que le joueur achève une partie, la plateforme lui propose une nouvelle partie selon le modèle suivant :
• si le joueur achève une partie de type A, la plateforme lui propose
de jouer à nouveau une partie de type A avec une probabilité de 0,8 ;
• si le joueur achève une partie de type B, la plateforme lui propose
de jouer à nouveau une partie de type B avec une probabilité de 0,7.
Pour tout entier naturel n supérieur ou égal à 1, on note An et Bn les évènements :
An : « la 𝑛-ième partie est une partie de type A. »
Bn : « la 𝑛-ième partie est une partie de type B. »
Pour tout entier naturel n supérieur ou égal à 1, on note an la probabilité de l’évènement An.
a. Recopier et compléter l’arbre pondéré ci-dessous..
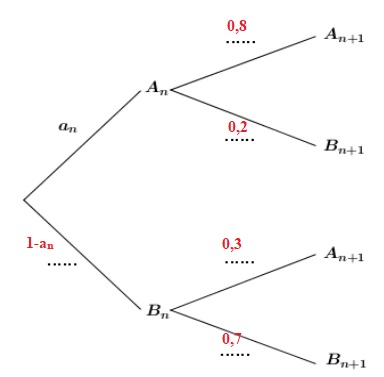
b. Montrer que pour tout entier naturel n≥ 1, on a : an+1 = 0,5 an +0,3.
D'après laformule des probabilités totales :
an+1 = 0,8 an +0,3(1- an) =0,5 an +0,3.
Dans
la suite de l’exercice, on note a la probabilité que le joueur joue au
jeu A lors de sa première partie, où a est un nombre réel appartenant à
l’intervalle [0; 1]. La suite (an) est donc définie par :
a1 = a et pour tout entier naturel n ≥ 1, an+1 = 0,5 an +0,3.
2. Étude d’un cas particulier : Dans cette question, on suppose que a = 0,5.
a. Montrer par récurrence que pour tout entier naturel n ≥ 1, on a : 0 ≤ an ≤ 0,6.
Initialisation : la propriété est vraie au rang 1
Hérédité : la relation est supposée vraie au rang p. 0 ≤ ap ≤ 0,6.
0 ≤0,5 ap ≤ 0,3 ; 0,3 ≤0,5 ap +0,3 ≤ 0,6 ; 0,3 ≤ ap+1 ≤ 0,6.
Par suite 0 ≤ ap+1 ≤ 0,6. La propriété est vraie au rang p+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout n > 1.
b. Montrer que la suite (an) est croissante.
an+1 -an = - 0,5 an +0,3.
Or 0 ≤ an ≤ 0,6 ; 0 ≤ 0,5an ≤ 0,3 ; 0 > -0,5an > -0,3 ; 0,3 > -0,5an +0,3> 0
an+1 -an > 0 ; la suite (an) est croissante.
c. Montrer que la suite (an) est convergente et préciser sa limite.
La suite est croissante et majorée par 0,6.
L = 0,3 +0,5 L ; 0,5 L = 0,3 ; L = 0,6.
3. Étude du cas général : Dans cette question, le réel a appartient à l’intervalle [0; 1].
On considère la suite (un) définie pour tout entier naturel n ≥ 1 par : un =an − 0,6.
a. Montrer que la suite (un) est une suite géométrique.
un+1 =an+1 − 0,6 = 0,5 an +0,3-0,6 =0,5 an -0,3 =0,5(an-0,6) = 0,5 un.
Par suite, (un) est géométrique de raison 0,5 et de premier terme u1=a-0,6.
b. En déduire que pour tout entier naturel n ≥ 1 on a : an = (a − 0,6) × 0,5n-1 + 0,6.
un =(a-0,6) 0,5n-1 =an − 0,6 ; an = (a − 0,6) × 0,5n-1 + 0,6.
c. Déterminer la limite de la suite (an). Cette limite dépend-elle de la valeur de a ?
0,5n-1 tend vers zéro si n tend vers plus l'infini ; an tend vers o,6 quelle que soit la valeur de a.
d.
La plateforme diffuse une publicité insérée en début des parties de
type A et une autre publicité insérée en début des parties de type B.
Quelle devrait être la publicité la plus vue par un joueur s’adonnant
intensivement aux jeux vidéo ?
Au bout d'un temps assez grand, la probabilité de jouer la partie A est
égale à 0,6 et la probabilité de jouer la partie B vaut 0,4.
Le joueur des parties A verra le plus souvent la publicité.
|
|
|
|
Exercice 3 : Commun à tous les
candidats (4 points)
Les quatre questions de cet exercice sont indépendantes.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.
Une réponse non justifiée n’est pas prise en compte. Une absence de réponse n’est pas pénalisée.
1. Dans l’ensemble C des nombres complexes, on considère l’équation (E) ∶ z2-2 *3½z +4 =0.
On note A et B les points du plan dont les affixes sont les solutions de (E).
Affirmation 1 : Le triangle OAB est équilatéral. Vrai.
Discriminant : D = 12-16 = -4 = 4 i2.
Solutions : z = 3½± i.
Le module de zA = 3½+ i. vaut 2 ; le module de zB = 3½- i. vaut 2 ; donc OA = OB.
zB-zA = -2i ; le module de zB-zA vaut 2 ; donc OA = OB=AB.
2. On note u le nombre complexe : u=3½+i et on note 3½-i son conjugué.
Affirmation 2 : 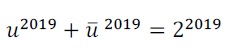 Faux. Faux.
u = 2 (3½ / 2 +0,5 i) =2 cos (p/6) + i sin (p/6)= 2 exp (ip/6) ;
u2019 = 22019 exp (i 2019 p/6) = 22019 exp (i 2019 p/6) =22019 exp (i (336p +3 p/6)) =22019 exp (i p/2).=22019 i.
Conjugué de u : 2 exp (- i p/6) ;
conjugué de u exposant 2019 = 22019 exp ( - i 2019 p/6) =22019 exp(- i (336p +3 p/6)) =22019 exp ( -i p/2).=22019 (-i)
.
3. Soit n un entier naturel non nul. On considère la fonction fn définie sur l’intervalle [0;+∞[ par :
fn(x) =x e-nx+1.
Affirmation 3 : Pour tout entier naturel n ≥ 1, la fonction fn admet un maximum. Vrai.
Dérivée : fn ' (x) = e-nx+1-nx e-nx+1 = e-nx+1(1-nx).
La dérivée s'annule pour x = 1 / n.
La dérivée est positive pour x < 1 / n ; la dérivée est négative pour x > 1 / n.
La fonction est croissante sur [0 ; 1 /n [ et décroissante sur [1 / n ; +oo[.
4. On note 𝒞 la courbe représentative de la fonction 𝑓 définie sur R par : f(x)= cos((x) e-x.
Affirmation 4 : La courbe 𝒞 admet une asymptote en +oo. Vrai.
-1 < cos (x) < 1 ; e-x est positif.
e-x tend vers zéro si x tend vers plus l'infini.
-e-x < cos (x)e-x < e-x ;
Appliquer le théorème d'encadrement : cos (x)e-x tend vers zéro si x tend vers plus l'infini.
5. Soit A un nombre réel strictement positif.
On considère l’algorithme ci-dessous :
I = 0
Tant que 2I < A
I = I+1
Fin Tant que
On suppose que la variable I contient la valeur 15 en fin d’exécution de cet algorithme.
Affirmation 5 : 15 ln(2) ≤ ln(A) ≤ 16 ln(2). Faux.
214 < A et 2 15 > A ; 214 < A < 215 ;
La fonction logarithme est strictement croissante sur R*+
ln 214 < ln A < ln215 ; 14 ln 2< ln A <15 ln 2
|
|
Exercice 4
5 points
On considère un cube ABCDEFGH d’arête de longueur 1, dont la figure est donnée.
On note I le milieu du segment [EF], J le milieu du segment [EH] et K le point du segment [AD].
On note P le plan passant par I et parallèle au plan (FHK).
Partie A.
Dans cette partie, les constructions demandées seront effectuées sans justification..
1. Le plan (FHK) coupe la droite (AE) en un point qu’on note M. Construire le point M.
2. Construire la section du cube par le plan P.
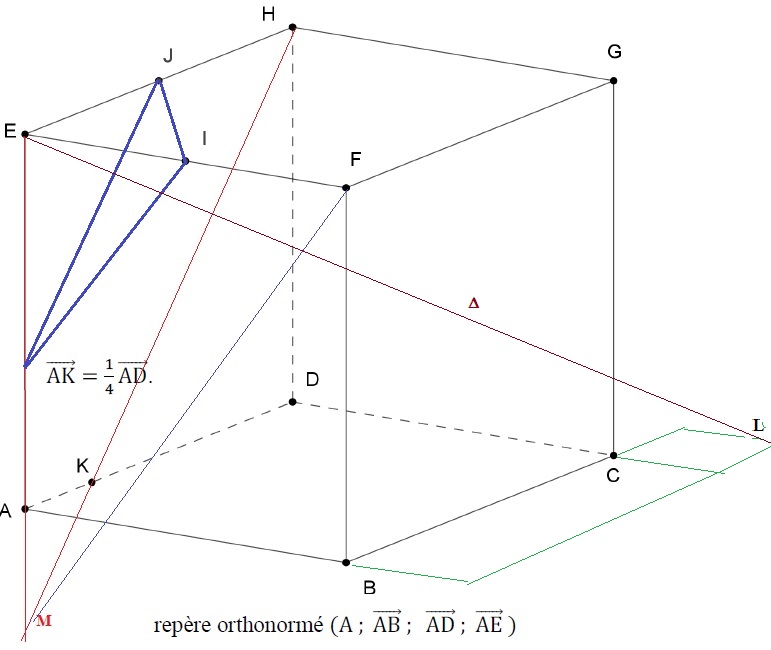
Les droites (HK) et (AE) sont incluses dans le plan (AEH). Ces droites se coupent en M.
Dans le triangle HEF, la droite passant par I et J, milieux des cotés
EF et EH, est parallèle à la droite (HF). C'est la droite des
milieux.
L'intersection des plans (AEF) et (FHK) est la droite (FM).
Le plan P et le plan (ABF) est une droite parallèle à la droite (FM), passant par I.
Partie B.
Dans cette partie, on munit l’espace du repère orthonormé.
On rappelle que P est le plan passant par I et parallèle au plan (FHK).
1. a. Montrer que le vecteur 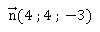 est un vecteur normal au plan (FHK). est un vecteur normal au plan (FHK).
b. En déduire qu'une équation cartésienne du plan (FHK) est : 4𝑥 + 4𝑦 − 3𝑧 − 1 = 0.
Equation de ce plan : ax +by +cz +d = 0.
F(1 ; 0 ; 1) appartient à ce plan : a +c +d = 0.
H(0, 1 , 1) appartient à ce plan : b +c+d = 0 ; par suite a=b.
K(0 ; 0,25 ; 0) appartient à ce plan : 0,25 b +d = 0 ; soit d = -0,25 b= -0,25 a..
a +c-0,25a = 0 soit c = -0,75 a.
ax +ay -0,75az -0,25a = 0 ; x +y-0,75z -0,25 =0.
4x +4y -3z -1=0.
c. Déterminer une équation cartésienne du plan P.
P est le plan passant par I (0,5 ; 0 ; 1) et parallèle au plan (FHK).
Equation du plan P : 4x +4y -3z +d=0.
I appartient à ce plan : 2 -3+d=0 ; d = 1.
4x +4y -3z +1=0.
d. Calculer les coordonnées du point M′, point d’intersection du plan P et de la droite (AE).
A(0 ; 0 ; 0) ; E(0 ; 0 ; 1) ; 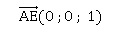
Equation paramètrique de la droite (AE) : z = t avec t réel.
M' appartient au plan P et à la droite (AE) : -3t+1 = 0 ; t = 1 /3.
M' (0 ; 0 ; 1/3).
2. On note Δ la droite passant par le point E et orthogonale au plan P.
a. Déterminer une représentation paramétrique de la droite Δ.
Coordonnées du vecteur directeur de cette droite : (4 ; 4 ; -3).
La droite passe par E(0 ; 0 ; 1) :
x = 4t ; y = 4t ; z = -3t+1 avec t réel.
b. Calculer les coordonnées du point L, intersection de la droite Δ et du plan (ABC).
Equation cartésienne du plan (ABC) : z = 0.
Par suite t = 1 /3.
xL =4 /3 ; yL = 4 /3 ; zL =0 ; L(4 /3 ; 4 /3 ; 0).
c. Tracer la droite Δ sur la figure donnée.
d. Les droites Δ et (BF) sont-elles sécantes ? Qu’en est-il des droites Δ et (CG) ? Justifier.
Les points B, E et F appartiennent au plan (ABE) ; L n'appartient pas à ce plan.
Les droites Δ et (BF) ne sont pas sécantes.
Hypothèse : les droites Δ et (CG) sont sécantes.
On cherche les coordonnées du point N, intersection des droites D et CG :
D : x = 4t ; y = 4t ; z = -3t+1 ; (CG) : x = 1 ; y = 1 ; z = k avec k et t réels.
Par suite t = 0,25 ; k = 0,25 et N (1 ; 1 ; 0,25).
L'hypothèse est vraie.
|
|
|