Mathématiques,
bac S Métropole septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
| .
. |
......
.....
|
Exercice 1.
4 points
Lors d’un examen professionnel, chaque candidat doit présenter un
dossier de type A ou un dossierde type B ; 60% des candidats présentent un dossier de type A, les
autres présentant un dossier de type B.
Le jury attribue à chaque dossier une note comprise entre 0 et 20. Un
candidat est reçu si la note attribuée à son dossier est supérieure ou égale à 10. On choisit au hasard un dossier.
On admet qu’on peut modéliser la note attribuée à un dossier de type A
par une variable aléatoire X suivant la loi normale d’espérance 11,3 et d’écart-type 3, et la note
attribuée à un dossier de type B par une variable aléatoire Y suivant la loi normale d’espérance 12,4 et
d’écart type 4,7.
On pourra noter A l’évènement : « le dossier est un dossier de type A
», B l’évènement : « le dossier est un dossier de type B », et R l’évènement : « le dossier est celui d’un
candidat reçu à l’examen ».
Les probabilités seront arrondies au centième.
1. Le dossier choisi est de type A. Quelle est la probabilité que ce
dossier soit celui d’un candidat reçu à l’examen ?
p(X > 10) =1-P(X < 10) =1-0,332 ~0,67.
On admet que la probabilité que le dossier choisi,
sachant qu’il est de type B, soit celui d’un candidat reçu est égale à 0,70.
2. Montrer que la probabilité, arrondie au centième, que le dossier
choisi soit celui d’un candidat reçu à l’examen est égale à 0,68.
Formule des probabilités totales : 0,67 x0,60 +0,40 x0,70 ~0,68.
3.
Le jury examine 500 dossiers choisis aléatoirement parmi les
dossiers de type B. Parmi ces dossiers, 368 sont ceux de candidats
reçus à l’examen. Un membre du jury affirme que cet échantillon n’est
pas représentatif.
Il justifie son affirmation en expliquant que dans cet échantillon, la
proportion de candidats
reçus est trop grande.
Quel argument peut-on avancer pour confirmer ou contester ses propos ?
n = 500 ; np = 500 x0,68 = 340 > 5 ; n(1-p) =500 x0,32 = 160 > 5.
On peut définir un intervalle de fluctuation asymptotique :
1,96 (0,68 x0,32 / 500)½ = 0,041.
Intervalle de fluctuation [0,68 -0,041 ; 0,68 +0,041] soit [0,63 ; 0,73].
Fréquence observée : 368 /500 ~0,736.
Cette fréquenc en' appartient pas à cet intervalle.
Au risque de 5 %, on confirme cette affirmation.
4. Le jury décerne un « prix du jury » aux dossiers ayant obtenu une
note supérieure ou égale à N, où N est un nombre entier. La probabilité qu’un dossier choisi au
hasard obtienne le « prix du jury » est comprise entre 0,10 et 0,15.
Déterminer le nombre entier N.
0,10 < 0,6 P(X > N) +0,4 P (Y > N) < 0,15.
0,6 P(X > 15) +0,4 P (Y > 15)~0,181.
0,6 P(X > 16) +0,4 P (Y > 16)~0,124.
0,6 P(X > 17) +0,4 P (Y > 17)~0,083.
N = 16.
|
...
|
|
Exercice 2. 6 points.
On donne ci-dessous la représentation graphique Cg dans un repère orthogonal d’une fonction g définie et continue sur R. La courbe Cg est symétrique par rapport à l’axe des ordonnées et se situe dans le demi-plan y > 0.
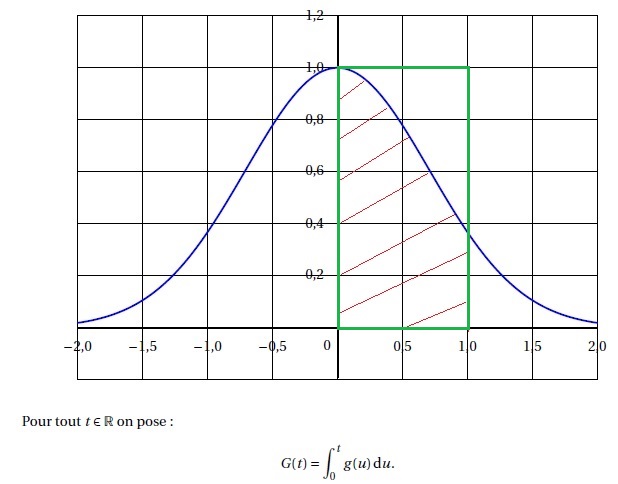
Partie A.
Les justifications des réponses aux questions suivantes pourront s’appuyer sur des considérations
graphiques.
1. La fonction G est-elle croissante sur [0 ; +∞[ ? Justifier.
g(x) est positive ou nulle pour tout x réel.
g(x) est la dérivée de la fonction G.
G est strictement croissante sur [0 ; +oo[.
2. Justifier graphiquement l’inégalité G(1) < 0,9.
G(1) est représentée par la partie hachurée soit environ 7 carreaux ou 7 x0,5 x0,2 =0,7.
3. La fonction G est-elle positive sur R ? Justifier.
G est strictement croissante sur [0 ; +oo[ et G(0) =0 ; donc G(t) > pour tout réel positif.
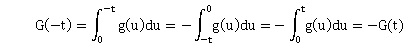
G(-t) est négative ; G n'est pas positive sur R.
Dans la suite du problème, la fonction g est définie sur R par g (u) = exp(−u2) .
Partie B.
1. Étude de g
a. Déterminer les limites de la fonction g aux bornes de son ensemble de définition.
u2 est positif ; -u2 est négatif.
Lorsque u tend vers ±-oo, -u2 tend vers moins l'infini et le terme en exponentielle tend vers zéro.
b. Calculer la fonction dérivée de g et en déduire le tableau de variations de g sur R.
g'(u)= -2u exp(−u2).
exp(−u2) étant toujours positif, le signe de g'(u) est celui de -u.
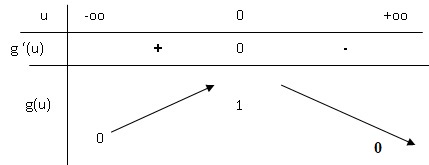
c. Préciser le maximum de g sur R. En déduire que g (1) <1.
Le maximum de la fonction g est égal à 1 en zéro.
Donc g(u) < 1 pour tout réel u.
2. On note E l’ensemble des points M situés entre la courbe Cg , l’axe des abscisses et les droites d’équation x = 0 et x = 1. On appelle I l’aire de cet ensemble.
On souhaite estimer l’aire I par laméthode dite « deMonte-Carlo » décrite ci-dessous.
- On choisit un point M(x ; y) en tirant au hasard de façon
indépendante ses coordonnées x et y selon la loi uniforme sur
l’intervalle [0 ; 1]. On admet que la probabilité que le point
M appartienne à l’ensemble E est égale à I .
- On répète n fois l’expérience du choix d’un point M au hasard. On
compte le nombre c de points appartenant à l’ensemble E parmi les n
points obtenus.
-La fréquence f = c / n est une estimation de la valeur de I .
a. La figure ci-dessous illustre la méthode présentée pour n = 100. Déterminer la valeur de f correspondant à ce graphique.
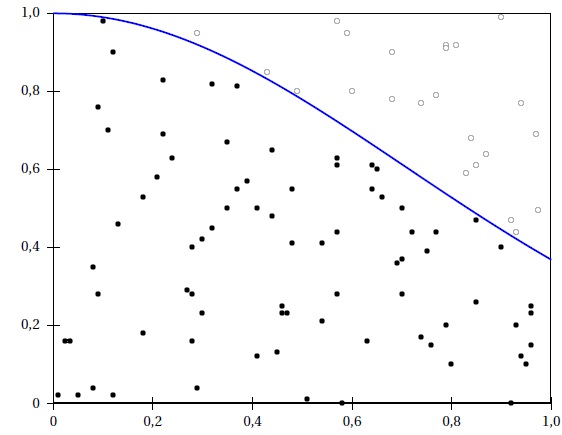
24 points en dehors soit c =76 ; f = 76 / 100 =0,76.
b. L’exécution de l’algorithme ci-dessous utilise la méthode de
Monte-Carlo décrite précédemment pour déterminer une valeur du nombre f
.
Recopier et compléter cet algorithme.
f , x et y sont des nombres réels, n, c et i sont des entiers naturels.
ALEA est une fonction qui génère aléatoirement un nombre compris entre 0 et 1.
c ←0
Pour i variant de 1 à n faire :
x ←ALEA
y ←ALEA
Si y < exp(-x2) alors
c ←c+1
fin Si
fin Pour
f ← c / n
c. Une exécution de l’algorithme pour n = 1000 donne f = 0,757.
En déduire un intervalle de confiance, au niveau de confiance de 95%, de la valeur exacte de I.
(1 /1000)½ =0,0316.
[0,757-0,0316 ; 0,757+0,0316] soit [0,725 ; 0,789 ]
Partie C.
On se propose de déterminer une majoration de G(t ) pour t >1.
1. Un résultat préliminaire.
On admet que, pour tout réel u >1, on a g (u) < 1 / u2 .
En déduire que, pour tout réel t >1, on a :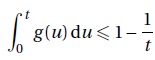
2. Montrer que, pour tout réel t >1, G(t ) < 2−1 / t..
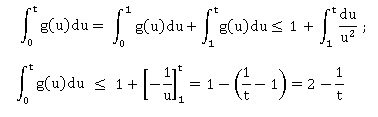
Que peut-on dire de la limite éventuelle de G(t ) lorsque t tend vers +∞?
1 / t tend vers zéro et G(t) tend vers 2.
|
....
|
Exercice 3.
5 points.
Préciser si chacune des affirmations suivantes est vraie ou fausse en justifiant votre réponse.
1. Soit m un nombre réel et soit l’équation (E) : 2z2 +(m−5)z +m = 0.
a. Affirmation 1 :
« Pour m = 4, l’équation (E) admet deux solutions réelles. » Faux.
2z2 -z +4 = 0. Discriminant : (-1)2-4 x4x2 = -31 < 0, donc deux solutions complexes.
b. Affirmation 2 : vrai.
« Il n’existe qu’une seule valeur de m telle que (E) admette deux solutions complexes qui soient des imaginaires purs. »
Discriminant : (m-5)2 -8m =m2 +25 -18m < 0 .
(m2 +25 -18m) i2 >0
Solutions : [ 5-m ± i(m2 +25 -18m)½] / 4.
Solutions imaginaires purs : 5-m = 0 ; m = 5.
2. Dans le plan complexe, on considère l’ensemble S des points M d’affixe z vérifiant :
|z −6| = |z +5i|.
Affirmation 3 :
« L’ensemble S est un cercle. » Faux.
On appelle A le point d'affixe 6 et B le point d'affixe -5i.
|z −6| = |z - (-5i)| est équivalent à AM = BM.
M appartient à la médiatrice su segment (AB].
3. On munit l’espace d’un repère orthonormé. On note d la droite dont une représentation paramétrique est :
d : x = −1+t ; y = 2−t ; z = 3+t avec t réel.
On note d′ la droite passant par le point B(4 ; 4 ;−6) et de vecteur directeur ayant pour coordonnées (5 ; 2 ; −9).
Affirmation 4 :
« Les droites d et d′ sont coplanaires. » vrai.
Les droites ne sont pas parallèles, car leurs vecteurs directeurs ne sont pas colinéaires.
Représentation paramétrique de la droite d' : x =5k+4 ; y = 2k +4 ; z = -9k -6 avec k réel.
Dans l'hypothèse où les droites sont sécantes, les coordonnées du point d'intersection sont :
-1+t = 5 k+4 ; t = 5k+5.
2-t = 2k+4 ; 2-5k-5 = 2k+4 ; 7k = -7 ; k = -1 et t =0.
-9 k-6 = 3 et 3+t = 3.
L'hypothèse de départ est donc vraie.
4. On considère le cube ABCDEFGH représenté ci-dessous.
Affirmation 5 : vrai.
« Le vecteur représenté en rouge est un vecteur normal au plan (ABG). »
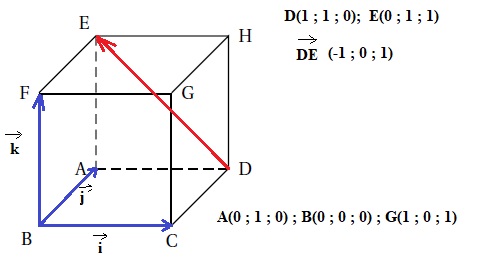
Equation du plan ABG : ax+by+cz+d=0.
B appartient à ce plan : d =0.
A appartient à ce plan : b = 0.
G appartient à ce plan : a +c = 0 ; c = -a.
ax -cz =0.
Coordonnées d'un vecteur normal à ce plan ( 1 ; 0 ; -1). Ce vecteur est colinéaire au vecteur de coordonnées (-1 ; 0 ; 1).
|
Exercice
4. 5 points
Soit f la fonction définie sur l’intervalle [0; 4] par f (x) =(2+3x) / (4+x).
Partie A
On considère la suite (un) définie par : u0 = 3 et pour tout entier naturel n, un+1 = f (un) .
On admet que cette suite est bien définie.
1. Calculer u1.
u1 = f(u0) = f(3) =11 / 7.
2. Montrer que la fonction f est croissante sur l’intervalle [0; 4].
On calcule la dérivée de f(x) en posant u = 2+3x et v = 4+x ; u' = 3 ; v' = 1.
f '(x) = [3(4+x) -(2+3x)] / (4+x)2 = 10 / (4+x)2 .
La dérivée étant positive, f(x) est croissante.
3. Montrer que pour tout entier naturel n,
1 < un+1 < un < 3.
Initialisation :
1 < u1 < u0 < 3 ;
1 < 11 / 7 < 3 < 3 est vraie.
Hérédité : la propriété est supposée vraie au rang n.
1 < un+1 < un < 3.
f est croissante sur [0 ; 4 ] : f(1) < f (un+1) < f(un) < f(3).
Soit
1 < un+2 < un+1 < 11 / 7 < 3.
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est vraie pour tout n.
4. a. Montrer que la suite (un) est convergente.
un+1 < un : la suite est décroissante ; de plus elle est minorée, donc elle converge.
b. On appelle ℓ la limite de la suite (un) ; montrer l’égalité :
ℓ =(2+3ℓ ) /(4+ℓ).
à la limite un =un+1 ; un = l ; un+1 = f(un) = f(
ℓ) =(2+3ℓ ) /(4+ℓ).
c. Déterminer la valeur de la limite ℓ.
4 l +l2 = 2+3l ; l2 + l- 2 =0 ; discriminant : 12 +4x2 = 9 ; solution retenue l =(-1+3) / 2 =1.
Partie B.
On considère la suite (vn) définie par :
v0 = 0,1 et pour tout entier naturel n, vn+1 = f (vn) .
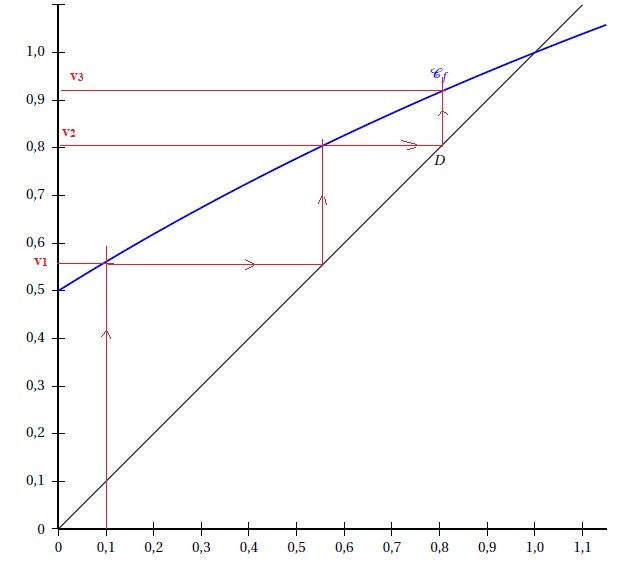
1. On donne la courbe représentative, Cf , de la fonction f et la droite D d’équation y = x.
Placer sur l’axe des abscisses par construction géométrique les termes v1, v2 et v3.
Quelle conjecture peut-on formuler sur le sens de variation et le comportement de la suite (vn) quand n tend vers l’infini ?
v1 = f(v0) = f(0,1) =(2+0,3) / (4+0,1) =2,3 / 4,1 = 23 /41~0,561
v2 = f(v1) = f(23 / 41) =(2+69 /41) / (4+23 /41) =(82+69) / 187 = 151 / 187~0,807.
v3 = f(v2) ~ f(0,807) =2,42 / 4,807 =0,920.
La suite est croissante et tend vers 1 quand n tend vers plus l'infini.
2. a. Montrer que pour tout entier naturel n,
1−vn+1 = 2(1−vn) /(4+vn).
1−vn+1 =1-f(vn) =1-(2+3vn) /(4+vn) =(4+vn-2-3vn) /(4+vn) =2(1−vn) /(4+vn).
b. Montrer par récurrence que pour tout entier naturel n,
0 < 1−vn < 0,5n.
Initialisation : la relation est vraie au rang zéro. ( 0,9 < 0,50 ; 0,9 < 1 )
Hérédité : la relation est supposée vraie au rang n. 0 < 1−vn < 0,5n.
1- vn+1 = 1- f(vn) =1- (2+3vn) /(4+vn)=2(1−vn) /(4+vn).
0 < 1−vn < 0,5n ; vn > 1-0,5n > 0
4 +vn > 4 ; 1 /(4 +vn ) < 0,25.
2(1−vn) / (4+vn) < 2 x 0,25 x0,5n ;
2(1−vn) / (4+vn) < 0,5n+1.
1- vn+1 < 0,5n+1. La propriété est vraie au rang n+1.
Conclusion : la proposition est vraie au rang zéro et héréditaire, donc elle est vraie pour tout n..
3. La suite (vn) converge-t-elle ? Si oui, préciser sa limite.
0 < 1−vn < 0,5n ; 0 > vn -1 > 0,5n ; 1 > vn > 1+0,5n ;
Quand n tend vers plus l'infini, 0,5n tend vers zéro. vn tend vers 1.
|
|
|