Mathématiques
bac S Polynésie septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
...
|
......
.....
|
Exercice 1.
6 points.
Deux groupes de scientifiques, des spécialistes en environnement et des
biologistes, étudient l’évolution d’une population de grenouilles
autour d’un étang.
Partie A — Étude d’un modèle discret d’évolution.
Le groupe de spécialistes en environnement étudie le taux de
disponibilité des ressources nécessaires pour le développement de la
population de grenouilles autour de l’étang. Ce taux dépend notamment
du nombre de grenouilles présentes sur les lieux, de la quantité de
nourriture à disposition, de l’espace disponible et de la qualité de
l’environnement.
Une étude, menée en 2018 par ce premier groupe de scientifiques, a
permis d’estimer le taux de disponibilité des ressources à 0,9 ; cela
signifie que 90 % des ressources sont disponibles.
On modélise le taux de disponibilité des ressources par la suite (Tn) qui, à tout entier naturel n, associe le taux de disponibilité des ressources n années après 2018. On a ainsi T0=0,9.
Le modèle choisi est tel que, pour tout entier naturel n, on a : Tn+1=Tn−0,1Tn2.
1. Certains
spécialistes en environnement estiment qu’en 2022, le taux de
disponibilité des ressources sera proche de 0,4. Cette affirmation
est-elle conforme au modèle ? Pourquoi ?
T1 = 0,9 -0,1 x0,92 =0,819.
T2 = 0,819 -0,1 x0,8192 ~0,752.
T3 = 0,752 -0,1 x0,7522 ~0,695.
T4 = 0,695 -0,1 x0,6952 ~0,647, valeur très différente de 0,4.
L'affirmation n'est pas conforme au modèle.
2. On définit la fonction
𝑓 sur l’intervalle [0 ;1] par f(x) = x-0,1 x2. Ainsi, la suite (Tn)
vérifie pour tout entier naturel n, Tn+1 = f(Tn)
a. Étudier les variations de la fonction f sur l’intervalle [0 ;1].
f '(x) = 1 -0,2x.
f '(x) = 0 si x = 5 ; sur l’intervalle [0 ;1] f '(x) est positive et f(x) est strictement croissante.
b. Montrer que pour tout n entier naturel, on a : 0 ≤ Tn+1 ≤ Tn ≤ 1.
Initialisation : T0 = 0,9 et T1 = 0,819.
0 ≤ T1 ≤ T0 ≤ 1.La propriété est vraie au rang 1.
Hérédité : la propriété est supposée vraie au rang p : 0 ≤ Tp+1 ≤ Tp ≤ 1.
La fonction f est strictement croissante sur l'intervalle [0 ; 1 ].
f(0) ≤ f(Tp+1 ) ≤ f(Tp )≤ 1.
0 ≤ Tp+2 ≤ Tp+1 ) ≤ 1. La propriété est vraie au rang p+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier n.
c. La suite (Tn) est-elle convergente ? Justifier la réponse.
La suite est décroissante et minorée par 0 : donc elle converge.
3. Le groupe de spécialistes en environnement affirme que, selon ce
modèle, le taux de disponibilité des ressources peut être inférieur à
0,4 au cours des vingt premières années qui suivent le début de l’étude
et qu’il est capable de déterminer en quelle année, ce seuil serait
atteint pour la première fois.
Cette affirmation est-elle conforme au modèle ? Pourquoi ?

T13 =0,40084 ; T14 =0,384.
En 2032 le seuil de 0,4 sera atteint. L'affirmation est conforme.
Partie B — Étude d’un modèle continu d’évolution.
Le groupe de biologistes a choisi une autre option et travaille sur le
nombre de grenouilles peuplant l’étang. Au 1er janvier 2018, il avait
été dénombré 250 grenouilles.
Les biologistes estiment que le nombre de grenouilles présentes autour
de l’étang peut être modélisé par la fonction P définie sur
l’intervalle [0 ; +∞[ par :
P(t)=1000 / (0,4+3,6 e−0,5𝑡 ) où t est le temps, mesuré en
années, écoulé depuis le 1er janvier 2018 (cette fonction découle d’un
modèle continu, usuel en biologie, le modèle de Verhulst).
1. Calculer P'(t) où P' est la fonction dérivée de P puis étudier le signe de P'(t) pour t appartenant à l’intervalle [0 ; +∞[.
On pose u =0,4+3,6 e−0,5t ; u' = -3,6 x0,5 e−0,5t = -1,8 e−0,5t .
P'(t) = -u' / u2 = -1000 x(-1,8 e−0,5t ) / (0,4+3,6 e−0,5t )2 = 1800 e−0,5t / (0,4+3,6 e−0,5t )2 .
La fonction exponentielle étant strictement positive sur R, P'(t) est positive et P(t) est strictement croissante.
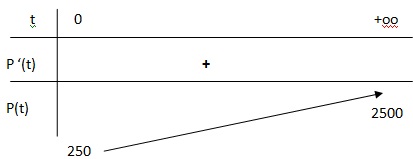
2. Déterminer la limite de la fonction P en +∞ puis dresser le tableau de variation de la fonction P sur l’intervalle [0 ; +∞[.
Quand t tend vers plus l'infini, e−0,5t tend vers zéro.
P(t) tend vers 1000 / 0,4 = 2500.
3. Montrer qu’il existe une unique valeur t0 ∈[0 ; +∞[ telle que P(t0)=2000. Déterminer cette valeur à 10−1 près.
La fonction P(t) est continue ( car dérivable ) et strictement croissante de 250 à 2500 sur cet intervalle.
D'après le théorème de la bijection, l'équation P(t) = 2000 admet une unique solution sur cet intervalle.
4. Selon ce modèle,
déterminer au cours de quelle année la population de l’étang aura
dépassé pour la première fois les 2000 grenouilles.
1000 / (0,4+3,6 e−0,5𝑡 ) = 2000 ; 0,5 = 0,4+3,6 e−0,5𝑡 ; 0,1 / 3,6 = e−0,5𝑡 ;
ln 36 = 0,5 t ; t =2 ln 36 ~ 7,16 ; t = 8 (année 2026).
|
...
|
|
Exercice
2. 5 points.
Dans cet exercice, les probabilités demandées seront précisées à 10−4 près.
Lors d’une communication électronique, tout échange d’information se
fait par l’envoi d’une suite de 0 ou de 1, appelés bits, et cela par le
biais d’un canal qui est généralement un câble électrique, des ondes
radio …
Une suite de 8 bits est appelé un octet. Par exemple, 10010110 est un octet.
Partie A.
On se place dans le cas où l’on envoie, sur le canal, successivement 8 bits qui forment un octet.
On envoie un octet au hasard. On suppose la transmission de chaque bit
indépendante de la transmission des bits précédents. On admet que la
probabilité qu’un bit soit mal transmis est égale à 0,01.
On note X la variable aléatoire égale au nombre de bits mal transmis dans l’octet lors de cette communication.
1. Quelle est la loi de probabilité suivie par la variable aléatoire X ? Justifier.
Les tirages sont identiques et indépendants les uns des autres. Il y a
deux issus possibles:le bit est bien transmis 1-p = 0,99 ; le bit est
mal transmis p = 0,01.
X suit une loi binomiale de paramètres n = 8 et p = 0,01.
2. Déterminer la probabilité qu’exactement deux bits de l’octet soient mal transmis.
P(X = 2) = 8 x7 / 2 x 0,012 x0,996=0,0026.
3. Que peut-on
penser de l’affirmation suivante : « La probabilité que le nombre de
bits mal transmis de l’octet soit au moins égal à trois est négligeable
» ? Argumenter.
P(X > 3)=1-P(X=2)-P(X=1)-P(X=0).
P(X = 1) = 8 x 0,01 x0,997=0,07456.
P(X = 0) = 1 x 1 x0,998=0,9227.
P(X > 3)=1-0,0026-0,07456-0,9227 ~
9,5 10-5. L'affirmation est vraie.
Partie B.
Les erreurs de transmission des bits sont liées à la présence de bruits parasites sur le canal de communication.
On admet que l’information d’un bit reçu, incluant le bruit, peut être
modélisée à l’aide d’une variable aléatoire continue qui suit une loi
normale dont l’espérance est liée à la valeur du bit envoyé.
On envoie un bit de valeur 1. On admet que l’information reçue d’un bit
de valeur 1 peut être modélisée par une variable aléatoire R qui suit
la loi normale d’espérance 1 et d’écart-type 0,3.
On considère que le bit reçu n’est pas correctement interprété lorsque la valeur de R est inférieure ou égale à 0,4.
Calculer la probabilité que le bit reçu ne soit pas correctement interprété.
P(R < 0,4) ~0,0228.
Partie C.
Afin de détecter si un ou plusieurs bits de l’octet sont mal transmis,
on utilise un protocole de détection d’erreur. Il consiste à ajouter, à
la fin de l’octet à transmettre, un bit, appelé bit de parité et qui
est transmis après les huit bits de l’octet.
On s’intéresse désormais à la transmission de l’octet suivi de son bit de parité.
Une étude statistique a permis d’obtenir que :
la probabilité que les huit bits (octet) soient transmis sans erreur vaut 0,922 ;
la probabilité que les huit bits (octet) soient transmis avec exactement une erreur vaut 0,075 ;
si les huit bits (octet) ont été transmis sans erreur, la probabilité que le bit de parité soit envoyé sans erreur vaut 0,99 ;
si les huit bits (octet) ont été transmis avec exactement une erreur,
la probabilité que le bit de parité ait été envoyé sans erreur vaut 0,9
;
si les huit bits (octet) ont été transmis avec au moins deux erreurs,
la probabilité que le bit de parité soit envoyé sans erreur vaut 0,99 ;
On choisit au hasard un octet suivi de son bit de parité. On considère les évènements suivants :
- Z : « les huit bits de l’octet sont transmis avec aucune erreur » ;
- E : « les huit bits de l’octet sont transmis avec exactement une erreur » ;
- D : « les huit bits de l’octet sont transmis avec au moins deux erreurs » ;
- B : « le bit de parité est transmis sans erreur ».
1. Compléter l’arbre pondéré suivant.
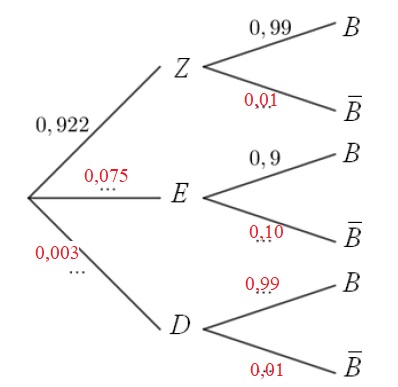
2. Quelle est la
probabilité que l’octet soit transmis avec une erreur exactement et que
le bit de parité soit transmis sans erreur ?
0,075 x 0,9 =0,0675.
3. Calculer la probabilité de l’événement B.
Formule des probabilités totales : p(B) = 0,922 x0,99 + 0,075 x0,9 +0,003 x 0,99 =0,91278 +0,0675 +0,00297 ~0,9833.
|
....
|
Exercice 3. 4 points
Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse.
Une réponse non justifiée n’est pas prise en compte.
1. On considère le nombre complexe 𝑍=1+i 3½.
Affirmation 1 : Le nombre complexe z2 est un réel positif. Faux.
Module de z : |z| = (12 +3)½ = 2.
z / |z| =0,5 + 0,5 i 3½ =cos (p/3 ) + i sin (p /3) ; z = 2 exp(ip/3).
z2 = 4 exp(i2p/3).
L'argument de z2 étant différent de 0 ou 2p, z2 n'est pas un réel positif.
Affirmation 2 : L’argument du nombre complexe 𝑍2019 vaut 0 modulo 2p. Faux.
p /3 x 2019 =673 p = p +336 x 2p.
Dans ce qui suit, le plan complexe est muni d’un repère orthonormé direct.
2. On considère dans C l'équation 2𝑧2−3𝑧+5=0.
Affirmation 3 : Cette équation admet deux solutions dont les images sont symétriques par rapport à l’origine du repère. Faux.
Discriminant D = (-3)2 -4 x2 x5= -31= 31 i2.
Solutions : z1 = (3+i 31½) / 4 ; z2 = (3-i 31½) / 4.
Les images de ces points sont symétriques par rapport à l'axe des abscisses.
3. À tout point M d’affixe 𝑧 du plan complexe, on associe le point M′ d’affixe 𝑧’ par définie par :
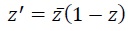 . .
Affirmation 4 : Il existe une infinité de points M confondus avec leur point image M′. Faux.
z = x +iy ; conjugué de z = x-iy ; la relation s'écrit :
z=z' ; x+iy =(x-iy)(1-x-iy)=x(1-x)-y2-i(y(1-x)+xy).
x+iy =x(1-x)-y2-iy.
soit pour les parties réeeles : x = x -x2-y2 ; x2+y2=0.
et pour les parties imaginaires : y = -y ; y =0. Par suite x = 0.
|
Exercice 4.
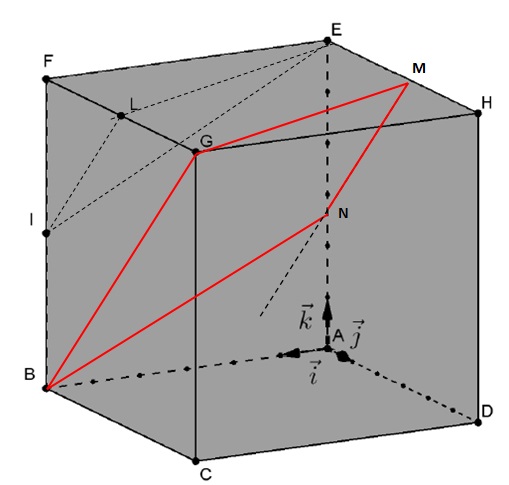
Sur la figure suivante, on considère le cube ABCDEFGH de côté 6 cm dans le repère orthonormé, l’unité étant le cm.
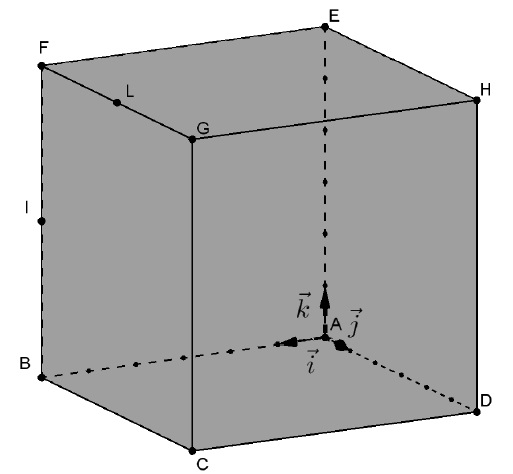
On admet que le point I a pour coordonnées (6 ;0 ;3) dans ce repère.
On appelle L le milieu du segment [FG].
On appelle P le plan défini par les trois points E, I et L.
On rappelle que le volume du tétraèdre est donné par la formule V =aire de la base × hauteur / 3.
1. a. Montrer que le vecteur 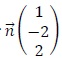 est un vecteur normal au plan P. est un vecteur normal au plan P.
E(0 ; 0 ; 6) ; I(6 ; 0 ; 3) ; L(6 ; 3 ; 6).
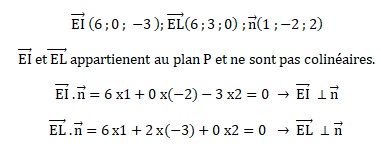
b. Déterminer une équation cartésienne du plan P.
x-2y+2z+d=0.
E appartient au plan P : 2x6+d=0 ; d=-12.
Equation cartésienne du plan P : x-2y+2z-12=0.
2. Justifier que le volume du tétraèdre FELI est 9 cm³.
Aire de la base = aire du triangle rectangle FEI = FE x FI / 2 = 6 x 3 / 2 = 9 cm2.
Hauteur du tétraèdre FL = 3 cm.
Volume du tétraèdre : V = 9 x3 / 3 = 9 cm3.
3. a. Soit Δ la perpendiculaire au plan P passant par le point F.
Justifier que la droite Δ admet pour représentation paramétrique :
{ x = t +6 ; y = -2t ; z =2t+6 } avec t réel.
Le vecteur 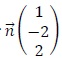 est un vecteur directeur de cette droite. est un vecteur directeur de cette droite.
Le point F (6 ; 0 ; 6) appartient à cette droite.
{ x = t +xF ; y = -2t +yF; z =2t+zF } avec t réel.
b. Montrer que l’intersection de la droite Δ et du plan P est le point K (16 /3 ; 4/ 3 ;14 / 3).
Les coordonnées du point K vérifient l'équation du plan P :
t +6-2(-2t)+2(2t+6)-12=0 ; 9t +6=0 ; t = -2 / 3.
xK = -2 / 3 +6 = 16 / 3 ; yK = -2 (-2 /3) = 4 /3 ; zK = 2 (-2 / 3) +6 = 14 / 3.
4. Calculer l’aire en cm² du triangle ELI.
FK = [ (6- 16 /3)2 +(0-4 /3)2 +(6-14 /3)2]½ =[ 4 /9 + 16 / 9 +16 / 9]2 =2 cm.
Aire du triangle ELI = 3 volume du tétraèdre / FK =27 /2 =13,5 cm2.
EL = (FE2 + FL2)½ =(62+32)½ =45½= 3 x5½.
IL = (FI2 + FL2)½ =(32+32)½ =18½=3 x2½.
Aire de ce triangle rectangle en L : 9 x 10½ / 2 =4,5 x10½ cm2.
5. Tracer
la section du cube ABCDEFGH par le plan parallèle au plan P passant par
le point G et en donner la nature précise sans justification.
On trace la parallèle à la droite (EL) passant par G ; elle coupe le segment [EH] en M.
La parallèle à la droite (IL) passant par G est la droite (BG).
La parallèle à la droite (BG) passant par M coupe le segment [AE] en N.
La section du cube par le plan P est le trapèze BGMN.
|
|
|



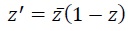 .
.
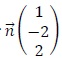 est un vecteur normal au plan P.
est un vecteur normal au plan P.