Mathématiques,
bac St2S Métropole septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. 6 points
PARTIE A : étude d’une fonction
On considère la fonction f définie sur l’intervalle [0; 12] par :
f (t )= 10 / (t+1).
1. On admet que la fonction dérivée f ′ de f est définie sur l’intervalle [0; 12] par :
f ′(t ) = −10 / (t +1)2 .
a. Expliquer pourquoi le signe de f ′(t ) est négatif sur l’intervalle [0; 12].
Le terme (t+1)2 est toujours positif.
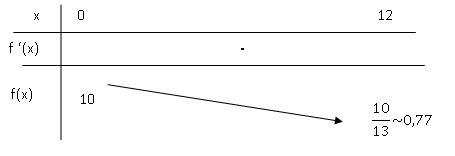
b. Établir le tableau de variation de la fonction f sur l’intervalle [0; 12].
On précisera dans le tableau les images de 0 et de 12 par la fonction f .
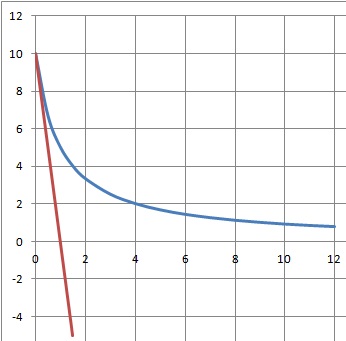
2. Compléter le tableau de valeurs de la fonction f . On arrondira si besoin à 10−1.
t
|
0
|
0,5
|
1
|
1,5
|
2
|
3
|
4
|
5
|
6
|
8
|
10
|
12
|
f(t)
|
10
|
6,7
|
5
|
4
|
3,3
|
2,5
|
2
|
1,7
|
1,4
|
1,1
|
0,9
|
0,8
|
3. Tracer la courbe (C) représentative de la fonction f .
4. a. Vérifier que f ′(0) = −10 et interpréter ce nombre géométriquement.
b. Tracer la tangente (T ) à la courbe (C) au point d’abscisse 0.
f'(0) = -10 /12 = -10.
Le coefficient directeur de la tangente à la courbe à l'origine est
égal à -10. Ce nombre, en valeur absolue, correspond à la vitesse de
disparition des bactéries.
PARTIE B : application
Dans le cadre d’une étude, un laboratoire expose une culture de bactéries à des rayons ultraviolets (UV).
Ces rayons ont un effet désinfectant et provoquent la diminution du nombre de bactéries.
On suppose que le nombre (en millions) de bactéries présentes au bout
du temps t (exprimé en heures) écoulé depuis le début de l’exposition
aux UV est donné par la fonction f définie sur [0; 12] par : f (t )= 10
/(t+1)..
On se servira de la partie A pour répondre aux questions suivantes :
1. Utilisation de la fonction f .
a. Déterminer le nombre de bactéries présentes au début de l’expérience.
10 millions.
b. Quel est le
temps nécessaire pour que soient éliminées 90% des bactéries présentes
au début de l’expérience? Préciser la méthode utilisée.
10 x0,1 = 1 million.
1= 10 / (t+1) ; t+1 = 10 ; t = 9 heures.
2. Utilisation de la fonction f ′.
On admet que, pour tout réel t de l’intervalle [0; 12], le nombre
dérivé f ′(t ) correspond à la vitesse d’évolution du nombre de
bactéries à l’instant t . Comparer les vitesses d’évolution du nombre
de bactéries aux instants 0 et 4. Auquel de ces deux instants la
décroissance est-elle la plus forte ?
f '(0) = -10 ; f '(4) =-10 / (1+4)2 =-0,4. La vitesse de disparition des bactéries est la plus forte pour t = 0.
|
...
|
|
Exercice 2. 6 points.
Les deux parties de cet exercice peuvent être traitées demanière indépendante.
Le tableau ci-dessous donne le nombre des unions civiles, PACS* ou
mariages, enregistrées en France entre 2005 et 2016. (PACS*. Pacte
Civil de Solidarité).
Année
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
2014
|
2015
|
2016
|
Rang de l'année
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
Nombre de mariages ( en milliers)
|
283
|
274
|
273
|
265
|
251
|
252
|
237
|
246
|
239
|
241
|
236
|
233
|
Nombre de PACS ( en milliers)
|
60
|
77
|
102
|
146
|
174
|
205
|
152
|
160
|
169
|
174
|
189
|
192
|
Source INSEE.
PARTIE A : étude de l’évolution du nombre demariages
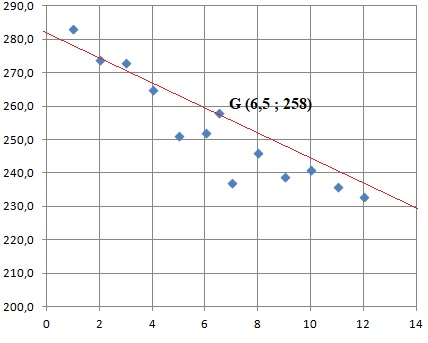
1. Représenter le nuage de points de coordonnées (xi ; yi ) où xi désigne le rang de l’année et yi le nombre demariages.
2. Calculer les coordonnées du point moyen G. Placer G dans le repère.
3. On réalise un ajustement affine de ce nuage à l’aide de la droite (d1) d’équation : y = −4,4x + 281,1.
Tracer la droite (dl) sur le graphique. Indiquer sur la copie les coordonnées des points utilisés.
4. On suppose que
ce modèle d’ajustement reste valable jusqu’en 2025. Déterminer le
nombre de mariages prévisibles en 2020. Préciser la démarche utilisée.
La droie (d) passe par le point G et le point de coordonnées (0 ; 281,1).
En 2025, x = 19 ; -4,4 x19 +281,1 ~198.
PARTIE B : comparaison des PACS et mariages
1.
D’après les indications du tableau, calculer la part exprimée en
pourcentage, arrondie à 1%, des mariages enregistrés en 2016 par
rapport à l’ensemble des unions civiles de cette même année.
Nombre d'unions civiles : 233 +192 = 425.
part des mariages : 233 / 425 x100 ~55 %.
2. On
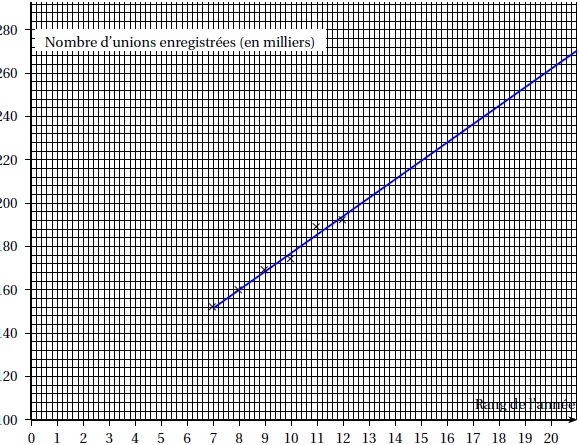
a représenté le nuage de points correspondant aux nombres annuels de
PACS à partir de l’année 2011. On a effectué un ajustement affine de ce
nuage de points à
l’aide de la droite (d2) d’équation : y = 8,5x +92.
On suppose que cet ajustement permet de modéliser jusqu’en 2025
l’évolution du nombre annuel y de PACS en fonction du rang x de l’année.
D’après ce modèle, à partir de quelle année le nombre de PACS sera-t-il
supérieur au nombre de mariages ? Expliquer la démarche employée.
8,5x +92 > −4,4x + 281,1 :
8,5x +4,4 x >281,1-92 ; 12,9 x > 189,1 ; x > 14,65 ( 15).
Année : 2005 +15 = 2020.
|
....
|
Exercice 3. 8 points.
Un cabinet d’orthophonie fait le bilan de son activité.
PARTIE A : évolution du nombre trimestriel de séances
Dans cette partie, on s’intéresse au nombre de séances d’orthophonie réalisées chaque trimestre au sein du cabinet.
Une feuille de calcul automatisée donne l’évolution du nombre de
séances réalisées du premier trimestre 2016 jusqu’au premier trimestre
2018 inclus.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
1
|
Année
|
2016
|
2017
|
2018
|
2
|
Trimestre
|
1
|
2
|
3
|
4
|
1
|
2
|
3
|
4
| 1
|
3
|
Nombre de séances
|
475
|
494
|
511
|
520
|
537
|
547
|
564
|
581
| 598
|
4
|
Taux d'évolution entre 2 trimestres consécutifs
|
|
4 %
|
|
|
|
|
|
|
|
Les cellules de la ligne 4, de C4 à J4, sont au format pourcentage.
1. Calculer le taux
d’évolution du nombre de séances entre le deuxième et le troisième
trimestre 2016. Le résultat sera arrondi à 0,1%.
(511-494) / 494 x100 = 3,4 %.
2. Proposer une
formule à saisir dans la cellule C4 qui, recopiée vers la droite,
permet de calculer le taux d’évolution du nombre de séances réalisées
par le cabinet d’orthophonie entre deux trimestres consécutifs.
=(C3-B3)/B3.
PARTIE B : modélisation de l’évolution
Dans cette deuxième partie, on considère que, à partir du premier
trimestre 2018, le nombre trimestriel de séances d’orthophonie
augmentera au rythme de 3% par trimestre. On modélise, à l’aide d’une
suite géométrique (rn), le nombre trimestriel de séances
réalisées par le cabinet, l’entier n désignant le nombre de trimestres
écoulés depuis le début de l’année 2018. Ainsi r1 = 598.
1. Justifier que la raison de la suite géométrique (rn) est égale à 1,03.
Chaque trimestre, le nombre de séances augmente de 3 %.
2. Calculer dans le cadre de cette modélisation le nombre de séances réalisées au cours du premier trimestre 2019.
n = 4 ; r4 = 598 x1,034 =673.
3. Résoudre, dans l’ensemble des réels, l’inéquation : 598×1,03x−1 >800.
1,03x-1 > 800 / 598.
(x-1) ln(1,03) > ln (800 / 598) ;
x-1 > ln(800 / 598)/ ln(1,03) ; x-1 >0,291 / 0,02956 ; x-1 > 9,84; x > 10,84 (~11).
4. Les
orthophonistes estiment qu’ils devront recruter un nouveau collègue
lorsque le nombre trimestriel de séances dépassera 800. Selon ce
modèle, déterminer le trimestre et l’année à partir desquels il faudra
faire ce recrutement.
Année 2020 ; fin du troisième trimestre.
PARTIE C : étude de la nature des prescriptions d’orthophonie
Dans cette dernière partie, on étudie, pour l’année 2016, les prescriptions de séances d’orthophonie.
On s’intéresse d’une part au type de prescripteur (médecin généraliste
ou spécialiste) et d’autre part à la nature de la pathologie traitée
selon trois catégories :
• troubles de l’articulation, de la parole ou du langage;
• dyslexie, dysorthographie, dyspraxie;
• autres pathologies.
On réalise cette étude sur un échantillon de 2 000 séances effectuées en 2016.
Il en ressort que :
• 79,9% des prescriptions ont été effectuées par un médecin généraliste ;
• parmi les séances prescrites par un médecin généraliste, la moitié concerne la dyslexie, la dysorthographie ou la dyspraxie ;
• un tiers des séances prescrites par un médecin spécialiste sont en
lien avec les troubles de l’articulation, de la parole ou du langage ;
• 55% des 380 séances associées aux autres pathologies sont prescrites par un médecin spécialiste.
1. Compléter le tableau suivant.
|
Généralistes
|
Spécialistes
|
Total
|
Troubles de l'articulation
de la parole ou du langage
|
1598-799-171=628
|
402 / 3 =134
|
762
|
Dyslexie, dyorthographie,
dyspraxie
|
1598 / 2 =799
|
402-134-209 = 59
|
858
|
Autres pathologies
|
380-209 =171
|
380 x 0,55 =209
|
380
|
Total
|
2000 x 0,799 =1598
|
2000-598 =402 |
2000
|
2. On choisit au hasard une séance dans l’échantillon. On définit les évènements suivants :
T : « la séance concerne un trouble de l’articulation, de la parole ou du langage » ;
D : « la séance concerne une dyslexie, une dysorthographie ou une dyspraxie » ;
A : « la séance concerne une autre pathologie » ;
G : « la séance est prescrite par un médecin généraliste ».
a. On considère PA(G). Traduire cette probabilité à l’aide d’une phrase.
Probabilité qu'une séance soit prescrite par un généraliste sachant qu'elle concerne une autre pathologie.
b. Calculer PA(G).
PA(G) =171 / 380 = 0,45.
c. Les évènements A et G sont-ils indépendants ? Justifier.
P(A) = 380 / 2000 =0,19 ; P(G) =1598 / 2000 =0,799 ; P(A n G) = 171 / 1598=0,107.
P(A n G) diffère de P(A) x P(G). Les événements A et G ne sont pas indépendants.
|
|