Math�matiques,
bac St2S Polyn�sie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
|
|
......
.....
|
Exercice 1.
5points.
Un
audioproth�siste compte parmi ses clients 75 % de personnes �g�es de
plus de 50 ans. Parmi celles-ci, 80 % souffrent de probl�mes d’audition
aux deux oreilles. Ce taux chute � 40 % parmi les clients de moins de
50 ans.
On choisit au hasard le dossier m�dical d’un client ; chaque dossier a
la m�me probabilit� d’�tre choisi.
On consid�re les �v�nements suivants :
• A : � le client est �g� de plus de 50 ans � ;
• D : � le client souffre de probl�mes auditifs aux deux oreilles �.
1. a. En utilisant
les donn�es fournies par l’�nonc�, donner les probabilit�s p(A) et P
non A (D).
P(A) =0,75 ; P non A (D)=0,40.
b. Recopier et compl�ter l’arbre
pond�r� de probabilit�s qui traduit la situation.
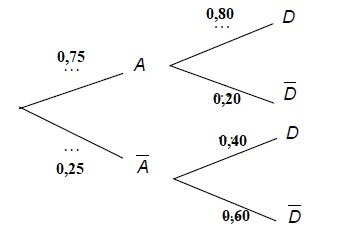
2. a. Calculer la
probabilit� que le client choisi ait plus de 50 ans et souffre de
probl�mes auditifs aux deux oreilles.
P(A nD) = 0,75 x0,80 = 0,60.
b. Montrer que la
probabilit� que le client choisi souffre de probl�mes auditifs aux deux
oreilles est �gale � 0,7.
Formule des probabilit�s totale :
P(A n D) + P(non
A nD) =0,60 + 0,25 x0,40 =0,70.
3. Le client choisi ne souffre pas
de probl�me auditif aux deux oreilles. Calculer la probabilit� qu’il
soit �g� de plus de 50 ans.
Pnon D(A) = P(non D n A) / P(non D).
P(non D) =0,75 x0,20 +0,25 x0,60 =0,15
+0,15 = 0,30.
P(non D n A) =0,75 x0,20 = 0,15.
Pnon D(A) =0,15 / 0,30 = 0,50.
|
...
|
|
Exercice 2.
(10 points)
Le dioxyde d’azote (NO2)
est un polluant indicateur des activit�s de combustion, notamment du
trafic routier. Pour la protection de la sant� humaine, les normes
europ�ennes fixent la valeur limite annuelle d’�mission de NO2
� 40 microgrammes par m�tre-cube.
On a report� dans la feuille de calcul ci-apr�s le nombre (en million)
d’habitants d’une r�gion urbaine potentiellement expos�e � un
d�passement de la valeur limite annuelle de NO2 entre 2010
et 2017. Ce d�passement est not� DVLA.
La ligne 4 est au format pourcentage, arrondi � 0,1 %.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
ann�e
|
2010
|
2011
|
2012
|
2013
|
2014
|
2015
|
2016
|
2017
|
2
|
rang
de l'ann�e (xi) |
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
3
|
nombre
d'habitants expos�s � un DVLA (yi) en millions.
|
2,9
|
2,7
|
2,6
|
2,6
|
2,4
|
1,6
|
1,5
|
1,3
|
4
|
taux
d�volution annuel ( %)
|
|
-6,9
|
|
|
|
|
|
|
Partie A.
1. Le nombre
d’habitants de cette r�gion en 2017 est estim� � 12,2 millions.
Calculer la proportion d’entre eux expos�s � un DVLA. Donner le
r�sultat en pourcentage, arrondi � 0,1 %.
1,3 x100 / 12,2 =10,7 %.
2. a. Calculer le
taux d’�volution global entre 2010 et 2017. Donner le r�sultat en
pourcentage, arrondi � 0,1 %.
(1,3 -2,9) x100 / 2,9 = -55,2 %.
b. Quelle formule
peut-on saisir dans la cellule C4 qui, recopi�e vers la droite, permet
de calculer les taux d’�volution du nombre d’habitants expos�s � un
DVLA entre deux ann�es cons�cutives ?
=(C3-B3)/B3
Partie B.
On a repr�sent� dans un rep�re orthogonal , le nuage de points de
coordonn�es (xi ; yi ).
1. Calculer les
coordonn�es du point moyen G puis le placer sur le graphique.
xmoyen =(0 +1 +2 +3 +4 +5 +6 +7) / 8 = 3,5.
ymoyen =(2,9 +2,7 +2,6 +2,6 +2,4 +1,6 +1,5 +1,3) / 8=2,2.
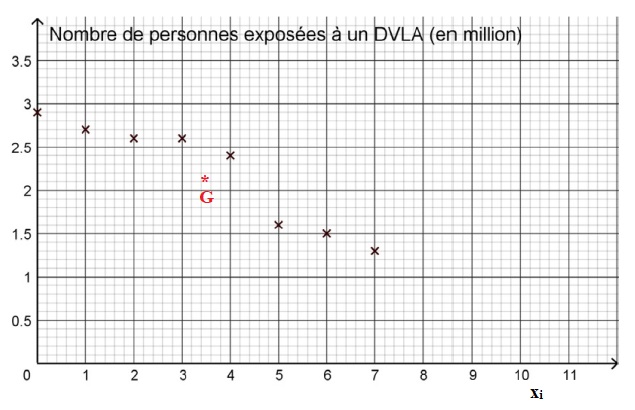
2. On admet que la
droite D d’�quation : y = − 0,26x + 3,11 r�alise un ajustement affine
du nuage de points jusqu’en 2022.
Estimer l’ann�e au cours de laquelle le nombre d’habitants expos�s � un
DVLA deviendra inf�rieur � 500 000. Justifier la r�ponse et pr�ciser la
m�thode utilis�e.
-0,26x +3,11< 0,5 ; 0,26x > 3,11 -0,5 =2,61 ; x > 2,61 /
0,26 ; x > 10,04 soit 11 . ( ann�e 2021 ).
Partie C.
Dans cette partie, on admet qu’� partir de 2015 et jusqu’en 2030 le
nombre d’habitants expos�s � un DVLA diminue de 10 % par an. On
mod�lise l’�volution du nombre d’habitants (en million) expos�s � un
DVLA par les premiers termes d’une suite (un ). Ainsi u0
= 1,6 .
1. a. Justifier que
la suite (un ) est une suite g�om�trique dont on pr�cisera
la raison.
On passe d'un terme au suivant en le multipliant par 0,9.
Il s'agit d'une suite g�om�trique de raison 0 ,9 et de premier terme
1,6.
b. Pour tout entier
n compris entre 0 et 15, exprimer un en fonction de n .
un = 1,6 x 09n.
2. Combien
d’habitants risquent d’�tre expos�s � un DVLA en 2019 ? Donner le
r�sultat en million arrondi au dixi�me.
n = 4 ; u4 = 1,6 x0,94 = 1,04976 ~1,0 million.
3. En d�taillant la
d�marche utilis�e, et dans le cadre de la mod�lisation par la suite (un
), d�terminer l’ann�e � partir de laquelle moins de 500 000 habitants
de la r�gion seront expos�s � un DVLA.
1,6 x 09n < 0,5 ; 0,9n
< 0,5 / 1,6 ; 0,9n < 0,3125.
n ln(0,9) < ln(0,3125) ; -0,1053 n < -1,163 ; n > 1,163
/ 0,1053 ; n >11,04 ; n > 12 ( ann�e 2027 ).
|
....
|
Exercice 3. 7 points.
Partie A.
On consid�re la fonction ƒ d�finie sur l’intervalle [0;15] par : ƒ(x) =
x3 − 21x2 +120x + 50 .
On note ƒ' la fonction d�riv�e de ƒ sur cet intervalle.
1. Calculer ƒ(4) et
ƒ(10).
f(10) = 103
-21 x100 +120 x10 +50=150.
f(4) =43 -21 x16 +120 x4 +50=258.
2. a. Calculer
ƒ'(x) .
f '(x) = 3x2-42x +120.
b. V�rifier que
pour tout r�el x de l’intervalle [0;15], on a : ƒ'(x) = (3x −12)(x −10)
.
(3x-12)(x-10) = 3x2-30x -12x+120 = 3x2-42x +120.
3. �tudier le signe
de ƒ'(x) sur l’intervalle [0;15] ; pour cela, recopier et compl�ter le
tableau de signes suivant :
x
|
0
|
|
4
|
|
10
|
15
|
signe
de (3x-12)
|
|
-
|
0
|
+
|
|
+
|
signe
de (x-10)
|
|
-
|
|
-
|
0
|
+ |
signe
de f '(x)
|
|
+
|
0
|
-
|
0
|
+
|
4. En d�duire le
tableau de variation de la fonction ƒ sur l’intervalle [0;15]. On
pr�cisera dans ce tableau, sans justification, les valeurs remarquables
de ƒ(x).
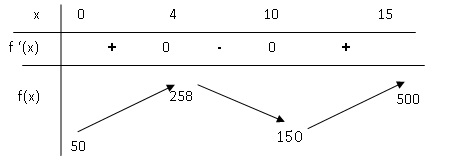
Partie B.
Des analyses ont montr� que des microalgues �taient naturellement
pr�sentes dans l’eau de mer, avec une concentration normale comprise
entre 0 et 100 milligrammes par litre (mg/L).
Ces microalgues ont tendance � se multiplier lorsque la salinit� de
l’eau de mer diminue, et les autorit�s sanitaires consid�rent qu’elles
deviennent dangereuses pour la sant�
lorsque leur concentration d�passe 200 mg/L. Il faut alors prendre des
mesures comme l’interdiction de la baignade.
La courbe donn�e mod�lise l’�volution de la concentration en
microalgues de l’eau de baignade d’une plage du littoral pendant les 10
jours qui ont suivi un tr�s fort
orage. Il s’agit de la courbe de la fonction ƒ �tudi�e dans la partie A
mais dont l’ensemble de d�finition est, dans cette partie B, restreint
� l’intervalle [0;10].
Pour chaque question suivante, justifier la r�ponse en pr�cisant la
m�thode utilis�e (calcul ou lecture graphique) et en expliquant la
d�marche ; pour la lecture graphique, laisser
apparents les pointill�s utiles.
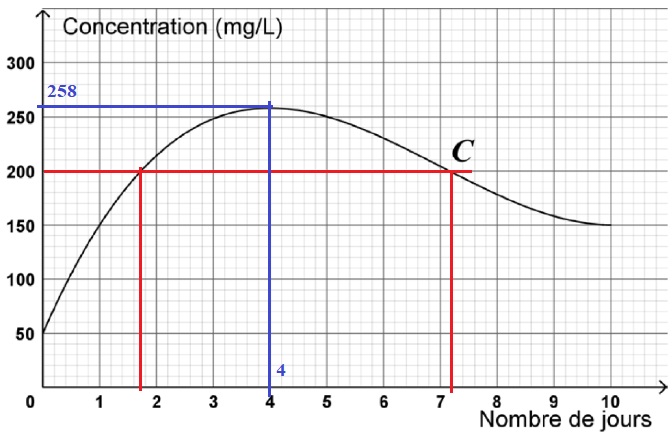
1. Pendant combien
de jours complets la baignade est-elle interdite ?
5,5 jours soit 6 jours.
2. Quelle est la
concentration maximale en microalgues durant les 10 jours suivant
l’orage ? Au bout de combien de jours a-t-elle �t� atteinte ?
258 mg / L le 4�me jour apr�s l'orage.
3. Peut-on
consid�rer que 10 jours apr�s l’orage, la situation est revenue � la
normale ?
Non, la concentration est �gale � 150 mg /L, valeur sup�rieure � 100 mg
/ L.
|
|
