Mathématiques,
bac Sti2D Métropole septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. 4 points
Cet
exercice est un questionnaire à choix multiples. Pour chacune des
questions suivantes, une seule des quatre réponses proposées est
exacte. Aucune justification n’est demandée.Une bonne réponse rapporte
un point. Une mauvaise réponse, plusieurs réponses ou l’absence de
réponse à une question ne rapportent ni n’enlèvent de point.
Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse.
1. Une variable aléatoire X suit la loi uniforme sur l’intervalle [2 ; 12].
P(X < 5) est égale à :
a. 0,5 ; b. 0,3 vrai ; c. 5 /12 ; d. 5 /7.
P(X < 5)= (5-2) / (12-2) = 3 / 10 = 0,3.
2. Une variable aléatoire X suit la loi normale d’espérance 20 et d’écart-type s.
P(X <18) peut être égale à :
a. 0,4 ; b. 1,8 ; c. 0,2 ; d. 0,82
Pour s = 2,37,
P(X <18) = 0,2 ; pour s = 7,9,
P(X <18) = 0,4 ;
3. La durée de vie, en années, d’un composant électronique est une variable aléatoire qui suit la loi exponentielle de paramètre l. La durée de vie moyenne de ce composant électronique est de 5 ans.
Le paramètre l vaut :
a. 5 ; b. 0,5; c. 0,2 vrai ; d. −0,2.
l =1 / 5 = 0,2.
4. Un argument du nombre complexe z = (2−2i )× exp( i p/2) est :
a. p /2 ; b. p /4 vrai ; c. 3p/4 ; d. 4 x 2½.
z1 = 2 -2i ; module (22 +22)½ =2 x 2½.
z1 / |z1| =1 / 2½ -i / 2½ =cos (-p /4) +i sin (-p /4).
arg(z) = p/2 -p /4 = p /4.
|
...
|
|
Exercice 2. 6 points.
Pour
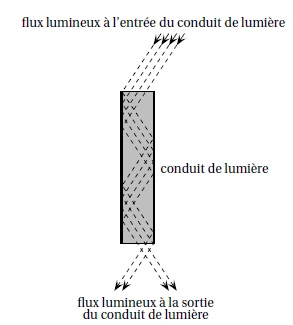
permettre un apport de lumière naturelle dans une habitation et
réaliser des économies d’électricité, une solution réside dans
l’installation d’un conduit de lumière au niveau de la toiture. Il
s’agit d’un tube cylindrique en aluminium recouvert d’un film
multicouche à base de polymère.
Dans ce conduit, le flux lumineux, exprimé en lumens (lm), diminue de 0,5% tous les décimètres.
On rappelle qu’un décimètre vaut dix centimètres.
Partie A.
Dans cette partie, on suppose que le flux lumineux à l’entrée d’un tel conduit de lumière est de 4 000 lumens.
On pose u0 = 4000. Pour tout entier naturel n supérieur ou égal à 1, on note (un) le flux lumineux, en lumens, à la sortie d’un conduit de longueur n décimètres.
1. Justifier que u1 = 3980.
Le flux lumineux, exprimé en lumens (lm), diminue de 0,5% tous les décimètres.
4000 x 0,995 =3980 lm.
2. Calculer le flux lumineux, en lumens, à la sortie d’un conduit d’une longueur de 20 cm.
3980 x 0,995 =3960,1 lm.
3. Justifier que la suite (un) est une suite géométrique dont on précisera les éléments caractéristiques.
On passe d'un terme au suivant en le multipliant par 0,995.
Suite géométrique de raison 0,995 et de premier terme 4000.
4. Pour tout entier naturel n, exprimer un en fonction de n.
un = 4000 x0,995n.
5. Un conduit de lumière de 2 mètres de long permettrait-il d’obtenir un flux lumineux d’au moins 3 600 lumens en sortie ?
n = 20 ; u20 = 4000 x0,99520=3618 lm. Donc vrai.
6. On considère l’algorithme ci-dessous où n désigne un entier naturel et U un nombre réel.
n←0
U ←4000
Tant que U > 3000
n←n +1
U ←U ×0,995
Fin Tant que
a. Indiquer le contenu de la variable n à la fin de l’exécution de l’algorithme.
4000 x0,995n > 3000 ; 0,995n >0,75 ;
n ln(0,995) > ln(0,75) ; n < 57,4 ( 58)
n = 58.
b. Interpréter la réponse obtenue à la question précédente dans le contexte du conduit de lumière.
Si le trajet de la lumière dépasse 5,8 m, le flux lumineux est inférieur à 3000 lm en sortie.
Partie B.
Dans une pièce sombre, on souhaite remplacer un éclairage électrique
par l’installation d’un conduit de lumière d’une longueur de 4 mètres
pour obtenir en sortie un flux lumineux d’au moins 3 100 lumens.
1. Déterminer le flux lumineux nécessaire à l’entrée de ce conduit.
n = 40 ; 3100 = u0 x0,99540 ; u0 = 3100 / 0,99540 ~3788 lm.
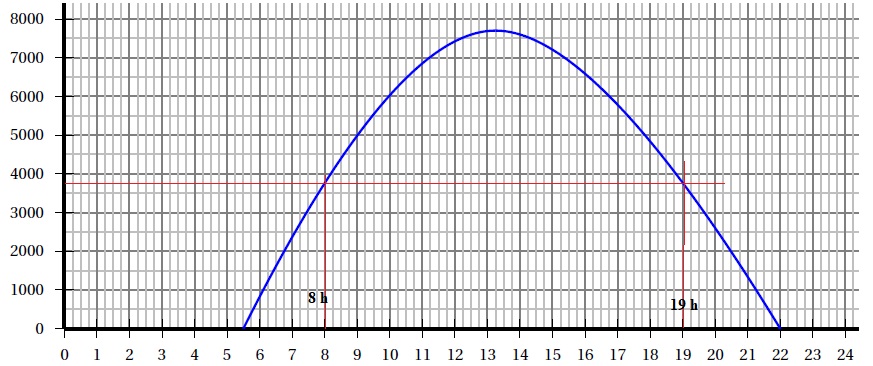
2. La
courbe ci-dessous modélise le flux lumineux, en lumens, à l’entrée de
ce conduit en fonction de l’heure pour une journée donnée.
Déterminer, avec la précision permise par le graphique, la plage
horaire durant laquelle ce flux lumineux à l’entrée du conduit est
suffisant.
|
....
|
Exercice 3. 5 points.
L’octane est un hydrocarbure qui entre dans la composition de l’essence.
Lorsqu’on chauffe un mélange d’octane et de solvant dans une cuve, une
réaction chimique transforme progressivement l’octane en un carburant
plus performant, appelé iso-octane. La concentration d’octane, en moles
par litre, dans la cuve est modélisée par une fonction f du temps t ,
exprimé en minutes. On admet que cette fonction f , définie et
dérivable sur l’intervalle [0 ; +∞[, est une solution, sur cet
intervalle, de l’équation différentielle suivante : (E) : y′ +0,12y =
0,003.
À l’instant t = 0, la concentration d’octane dans la cuve est de 0,5 mole par litre (mol.L−1).
1. a. Déterminer la solution générale de l’équation différentielle (E).
Solution générale de y' +0,12 y=0 : y = A exp(-0,12t) avec A une constante.
Solution particulière de E : y = 0,003 / 0,12 =0,025.
Solution générale de E : y = A exp(-0,12t) +0,025.
b. Donner f (0).
f(0) =A +0,025 = 0,5 ; A =0,475.
c. Vérifier que la fonction f est définie sur [0 ; +∞[ par f (t )= 0,475 exp (−0,12t) +0,025.
On dérive : f '(t) = 0,475 x(-0,12)exp (−0,12t) = -0,057 exp (−0,12t).
Repport dans (E) : -0,057 exp (−0,12t) +0,12(0,475 exp (−0,12t) +0,025) = 0,003.
-0,057 exp (−0,12t) +0,057 exp (−0,12t) +0,003 = 0,003 est vérifiée.
2. a. Calculer la fonction dérivée de la fonction f sur l’intervalle [0 ; +∞[.
f '(t) = 0,475 x(-0,12)exp (−0,12t) = -0,057 exp (−0,12t).
b. Étudier le sens de variation de la fonction f sur l’intervalle [0 ; +∞[.
Le terme exp (−0,12t) est toujours positif ; f '(t) est toujours négative.
f(t) est strictement décroissante sur l’intervalle [0 ; +∞[.
c. Interpréter cette réponse dans le contexte de l’exercice.
La concentration en octane diminue au cours du temps jusqu'à la valeur 0,025 mol /L.
3. Calculer, en
justifiant votre réponse, à la minute près, le temps nécessaire pour
obtenir une concentration en octane dans la cuve de 0,25 mole par litre.
0,25 = 0,475 exp (−0,12t) +0,025 ;
0,225 = 0,475 exp (−0,12t) ;
exp (−0,12t) =0,225 / 0,475 =0,4736 ;
-0,12 t = ln(0,4736) = -0,7472 ; t ~ 6 minutes.
4. a. Calculer, en justifiant votre réponse, la limite de f(t) en plus l'infini. Interpréter le résultat dans le contexte.
Le terme exp (−0,12t) tend vers zéro si le temps devient très long.
f(t) tend vers 0,025 en plus l'infini.
La concentration résiduelle en octane est 0,025 mol /L.
b. Le processus de transformation de l’octane en iso-octane est arrêté au bout d’une heure. Expliquer ce choix.
0,475 exp (−0,12 x60) ~3,54 10-4 ;
f(60) ~0,025 +3,54 10-4 ~ 0,02535 mol/L.
Au bout d'une heure, la réaction est pratiquement terminée.
|
Exercice 4. 5 points.
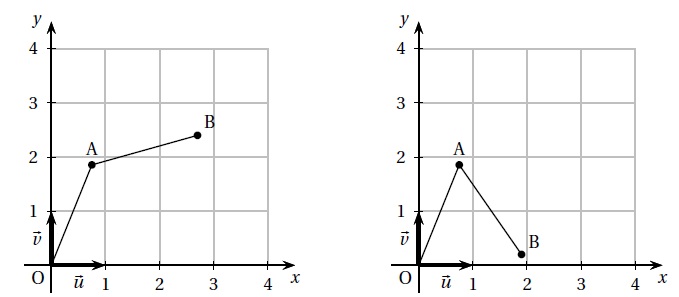
Dans le plan muni d’un repère orthonormé direct, le bras articulé d’un
robot, fixé au point O, est représenté par deux segments [OA] et [AB],
chacun de longueur 2 unités.
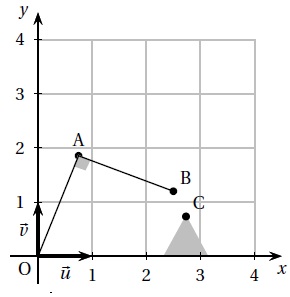
Deux exemples de position du bras articulé sont donnés ci-dessous à titre indicatif.
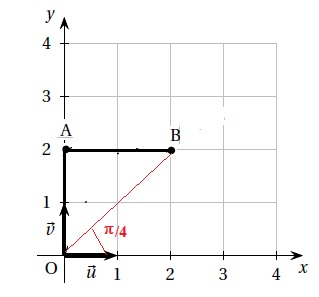
1. a. Tracer sur la copie un repère orthonormé.
Placer le point A d’affixe zA = 2i puis construire l’extrémité B du bras articulé lorsque son affixe zB a pour argument p /4.
b. Donner l’affixe du point B sous forme algébrique et sous forme exponentielle.
zB = 2 + 2i .
Module de zB : [22 +22]½= 2 x 2½.
zB = 2 x 2½ exp(ip/4).
2. L’extrémité B du bras peut-elle atteindre un objet qui se trouve à une distance de 4,5 unités du point O ?
2 x 2½ ~2,8 unités.
L'objet ne peut pas être atteint.
3. Pour
soulever un objet lourd dont le point d’accroche est le point C, il
faut rigidifier l’articulation en A. On décide alors de bloquer
l’angle(OAB) tel qu’une mesure de
cet angle soit constamment égale à 90°.
a. Déterminer la longueur OB.
Le triangle OAB est rectangle en A. OA = AB = 2 unités.
Le triangle OAB est rectangle isocèle.
OB = OA x2½=2 x2½.
b. Le point C a pour affixe zC = 2 x 2½ exp(ip /12).
Justifier que l’extrémité B du bras articulé pourra atteindre le point d’accroche C de l’objet.
OB = 2 x2½ ; OC = 2 x2½ .
c. Lorsque le bras articulé saisit l’objet, les points B et C sont confondus.
Calculer la mesure de l’angle que forme alors le bras [OA] avec l’axe [Ox).
Le triangle OAC est rectangle en A. OA = AC = 2 unités.
Le triangle OAC est rectangle isocèle. Les angles aigus mesurent p /4 radian.
Mesure de l’angle que forme alors le bras [OA] avec l’axe [Ox) :
p /4 +p /12 =4p /12 =p /3 radians. |
|
|