Math�matiques, bac Sti2D  Antilles septembre 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


.
.
......


.....

Exercice 1. 4 points
Cet exercice est un questionnaire � choix multiples. Pour chacune des questions suivantes, une seule des quatre r�ponses propos�es est exacte. Aucune justification n’est demand�e. Une bonne r�ponse rapporte un point. Une mauvaise r�ponse, plusieurs r�ponses ou l’absence de r�ponse � une question ne rapportent ni n’enl�vent aucun point.
Indiquer sur la copie le num�ro de la question et la r�ponse correspondante choisie.
1. On consid�re une fonction f dont le tableau de variations et le tableau de signes sont donn�s ci-dessous :

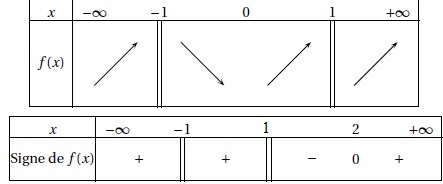
Une courbe susceptible de repr�senter la fonction f est :

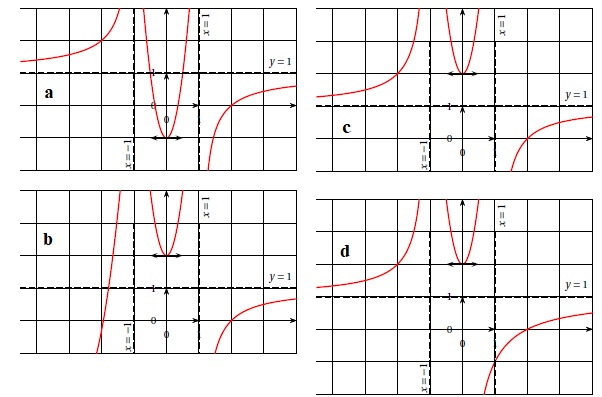
b. exclu : f(x) est positive sur l'intervalle ] -oo  ; -1].
a. exclu : f(x) positive sur l'intervalle [-1 ; 0].
d. exclu, la droite d'�quation x = 1 n'est pas asymptote.
R�pponse c.
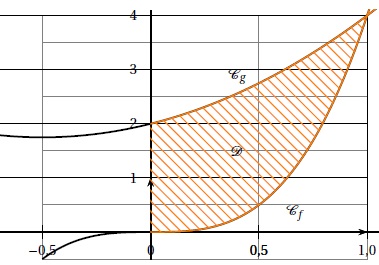
2. On consid�re f et g deux fonctions d�finies sur R par :
f (x) = 4x3 et g (x)= x2+x +2.
On note :
• Cf et Cg les courbes repr�sentatives respectives des fonctions f et g .
• D le domaine d�limit� par les courbes Cf et Cg , l’axe des ordonn�es et la droite d’�quation x = 1.
L’aire du domaine D, exprim�e en unit� d’aire, est �gale � : 31 / 24 ; 31 /12 ; 15 / 8 ; 11 / 6.

Primitive de f(x) entre 0 et 1 : [x4]0 1 =1.
Primitive de g(x) entre 0 et 1 : [x3/3 +0,5 x2 +2x]0 1 =1/3 +1 /2 +2 =.2 /6 +3 /6 +12/6 =17 / 6.
Faire la diff�rence : 17 /6 -1= 11 /6.
3. Le graphique ci-dessous donne la courbe repr�sentative de la densit� d’une variable al�atoire suivant une loi normale de param�tres μ et s. L’aire du domaine gris� est environ �gale � 0,68.

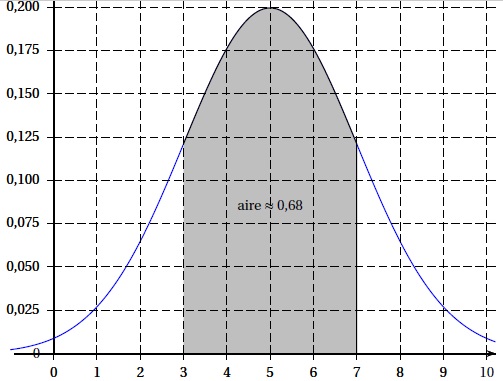
� partir de ce graphique, on en d�duit que :
a. μ = 2 et s = 5
b. μ = 0,2 et s = 5
c. μ = 5 et s= 1
d. μ = 5 et s = 2. Vrai.
4. Soit a un nombre r�el. La variable al�atoire X suit la loi uniforme sur [3 ; a].
On sait que p(X < 7) = 0,8.
La valeur de a est :7,2 ; 9 ; 8 ; 8,2.
p(X < 7) = (7-3) / (a-3)=0,8 ; 4 = 0,8a -2,4 ; 0,8 a = 6,4 ; a = 8.

...

Exercice 2. 5 points.
Les abeilles assurent la reproduction de plus des trois-quarts des esp�ces v�g�tales du globe terrestre gr�ce � la pollinisation. Depuis une dizaine d’ann�es, on constate une diminution du nombre de colonies d’abeilles � cause de l’�volution du climat et de l’utilisation d’insecticides pour prot�ger certaines cultures.
Partie A.
On observe une colonie constitu�e de 40 000 abeilles.On estime que, dans cette colonie, 1 000 abeilles naissent chaque jour et 500 d�c�dent chaque jour de mani�re naturelle. D�terminer, en justifiant, le nombre de jours n�cessaires pour que la population de cette colonie atteigne les 50 000 individus.
On note x le nombre de jours : 40 000 +1000x -500 x = 50 000 ;
500 x = 10 000 ; x = 20.
Partie B.
Apr�s ce premier temps d’observation, un insecticide est r�guli�rement pulv�ris� dans le champ pr�s duquel les abeilles butinent.
On estime alors � 20 % la proportion d’abeilles de la colonie qui d�c�dent chaque jour � cause de cet insecticide. On suppose que le nombre de naissances et de d�c�s de mani�re naturelle reste identique (1 000 naissances et 500 d�c�s demani�re naturelle). Pour tout entier naturel n, on note un le nombre d’individus de la colonie n jours apr�s le d�but des pulv�risations de l’insecticide. On a donc u0 =50000.
1. On mod�lise cette situation par la suite (un) d�finie pour tout entier naturel n par :
un+1 = 0,8un +500.
Calculer le nombre d’abeilles dans la colonie un jour apr�s le d�but des pulv�risations.
u1 = 0,8 u0 +500 = 40 500.
2. On consid�re la suite (vn) d�finie pour tout entier naturel n par : vn = un −2500.
a. Montrer que, pour tout entier naturel n : vn+1 = 0,8vn.
vn+1 = un+1 −2500 =0,8un +500 -2500 =0,8un -2000=0,8(vn-2500)=0,8vn.
b. En d�duire la nature de la suite (vn) et exprimer vn en fonction de n pour tout entier naturel n.
Suite g�om�trique de premier terme v0 = u0-2500 = 47500 et de raison q = 0,8.
vn = 47500 x0,8n.
c. En d�duire que, pour tout entier naturel n, on a : un = 47500�0,8n +2500.
un = vn +2500 =47500�0,8n +2500.
3. Des �tudes ont montr� qu’une colonie d’abeilles n’est plus en mesure d’assurer sa survie si elle compte moins de 5 000 individus.
La colonie �tudi�e va-t-elle survivre? Justifier la r�ponse.
47500�0,8n +2500 < 5000 ; 47500�0,8n < 2500.
0,8n < 2500 / 47500 ; n ln(0,8) < ln(2500 / 47500) ; n > 13 jours.
Au bout de 13 jours, la colonie ne peut survivre.
Partie C.
Le but de cette partie est de valider, ou non, la proportion p = 0,2 d’abeilles qui d�c�dent chaque jour � cause de l’insecticide.
L’insecticide utilis� ici provoque la d�sorientation des abeilles, ce qui perturbe leur retour � la colonie et entra�ne leur mort.
Un matin, on �quipe 500 abeilles de la colonie, de puces �lectroniques. On constate le lendemain que, dans cet �chantillon de 500 abeilles, 102 sont d�c�d�es � cause de l’insecticide.
Cette observation est-elle compatible avec l’hypoth�se p = 0,2 au seuil de 95 % ?
n = 500 > 30 ; np = 500 x0,2 = 100 > 5 ; n(1-p) =500 x0,8 = 400. On peut d�finir un intervalle de fluctuation asymptotique au seuil de 95 %.
1,96 (0,2 x0,8 / 500)� =0,035.
Intervalle de fluctuation : [0,2 -0,035 ; 0,2 +0,035] soit [0,165 ; 0,235].
Fr�quence observ�e : 102 / 500 = 0,204.
Cette valeur appartient � l'intervalle pr�c�dent. L'observation est compatible.


....

 Exercice 3. 7 points.
Partie A.
 Dans cet exercice, on s’int�resse aux batteries des voitures �lectriques. La charge (�nergie restituable) est exprim�e en kilowattheure.
Conform�ment � l’usage commercial, on appelle capacit� la charge compl�te d’une batterie.
1. La puissance de charge P d’une borne de recharge, exprim�e en Watt (W), s’obtient en multipliant sa tension U, exprim�e en Volt (V), par son intensit� I, exprim�e en Amp�re (A). Dans la pratique, on consid�re que le temps T de charge compl�te d’une batterie vide, exprim� en heure (h), s’obtient en divisant la capacit� C de la batterie, exprim�e usuellement en kilowattheure (kWh), par la puissance de charge P de la borne de recharge exprim�e en kilowatt (kW).
On consid�re une batterie de la marque D ( 60 kWh).
D�terminer le temps de charge compl�te de cette batterie sur une borne de recharge " Rapide" ( U = 400 V; I = 63 A).
 Exprimer le r�sultat en heures et minutes.
60 / (0,4 x 63) =2,38 h ou 2 h 23 min.
2. Lors du branchement d’une batterie vide de marque A (22 kWh) sur une borne de recharge de type �Normal �(230 V ; 16 ou 32 A), la charge (en kWh) en fonction du temps (en heure) est mod�lis�e par une fonction f d�finie et d�rivable sur [0 ; +∞[, solution de l’�quation diff�rentielle :
y′ +0,55y = 12,1. (E).
a. R�soudre cette �quation diff�rentielle sur [0 ; +∞[.
Solution g�n�rale de y' +0,55 y = 0 : y = A exp(-0,55t) avec A une constante.
Solution particuli�re de (E) : y = 12,1 / 0,55 = 22.
Solution g�n�rale de (E) :  y = A exp(-0,55t) +22.
b. Justifier que f (0) = 0.
Initialement la batterie n'est pas charg�e.
c. Montrer que la fonction f est d�finie sur [0 ; +∞[ par : f (t ) = −22exp(−0,55t) +22.
f '(t) = 22 x0,55 exp(−0,55t)=12,1 exp(−0,55t).
Repport dans (E) :12,1 exp(−0,55t) +0,55(−22exp(−0,55t) +22) = 0,55 x22 = 12,1.
d. La dur�e de demi-charge est le temps n�cessaire pour que la batterie soit charg�e � 50%.
R�soudre sur l’intervalle [0 ; +∞[ l’�quation f (t ) = 11 et en d�duire la dur�e d’une demi-charge, exprim�e en heure et minute.
−22exp(−0,55t) +22 = 11 ;  -exp(−0,55t) +1 = 0,5 ; exp(−0,55t)=0,5.
-0,55 t = ln(0,5) ; t = ln(0,5) / (-0,55) ~1,26 h ou 1 h 16 min.
e. Dans la pratique, on consid�re que le temps de charge compl�te de ce type de batterie est d’environ 6 heures.
V�rifier l’affirmation " Apr�s 50 % du temps de charge compl�te, la batterie est � environ � 80% de sa capacit� de charge".
f(3) =−22exp(−0,55x 3) +22= -4,2 +22 ~17,8  kWh.
 17,8 / 22 x100 ~80,8 %.

Partie B.
Une thermistance est un composant �lectronique dont la r�sistance varie en fonction de la temp�rature et qui est utilis�, entre autres, comme capteur de temp�rature. Afin d’alerter les utilisateurs de cas de surchauffe, on munit les batteries de thermistances.
Un constructeur de thermistances indique que la valeur R, exprim�e en Ohm, de la r�sistance de celle-ci est donn�e, pour des temp�ratures q, exprim�es en degr� Celsius (�C) et comprises entre 0 �C et 120 �C, par :
R = −0,04q3+7,2q2−240q+3000.
On consid�re la fonction g d�finie sur [0; 120] par :
g (x) = −0,04x3+7,2x2−240x +3000.
1. a. Calculer g ′(x) o� g ′ est la d�riv�e de g .
g'(x) = -0,12x2+14,4x-240.
b. Dresser, en justifiant, le tableau de variations de g sur [0; 120].
 -0,12x2+14,4x-240 = 0 ; discriminant : 14,42 -4 *240*0,12=207,36-115,2 =92,16 ;
solutions  :(-14,4 -92,16�) / (2 x(-0,12)) =100
(-14,4 +92,16�) / (2 x(-0,12)) =20
g'(x) est n�gative sur [0 ; 20) et g(x) est d�croissante.
g'(x) est positive sur [20 ; 100) et g(x) est croissante.
g'(x) est n�gative sur [100 ; 120) et g(x) est d�croissante
c. En d�duire la r�sistance maximale et la temp�rature pour laquelle elle est atteinte.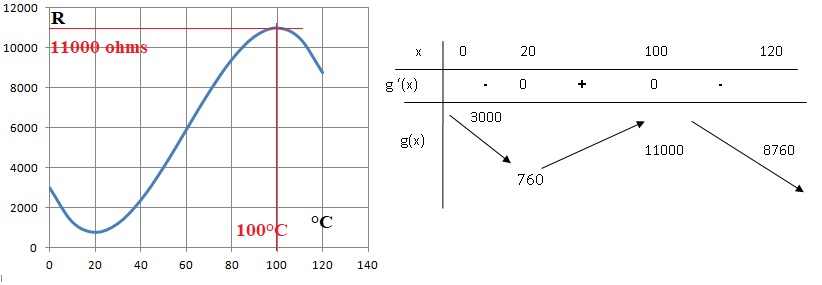

2. Un message d’alerte appara�t sur l’ordinateur de bord du v�hicule lorsque la r�sistance atteint 5 000 �ohms, ce qui signifie que la batterie est trop chaude. On cherche la temp�rature correspondant � cette valeur.
a. � l’aide de la calculatrice, donner un encadrement, � un degr� pr�s, de la temp�rature cherch�e.
55,4 �C.
b. On consid�re l’algorithme suivant :
x ←20
y ←760
Tant que y < 5000
x ←x +1
y ←−0,04x3+7,2x2−240x +3000
Fin Tant que
Recopier et compl�ter l’algorithme pour qu’� la fin de son ex�cution, la variable x contienne la temp�rature cherch�e.
 

Exercice 4. 4 points.
On note i le nombre complexe de module 1 et d’argument p /2.
1. On consid�re le nombre complexe z1 =2� exp(ip/4).
a. �crire z1 sous forme alg�brique.
z1 =2� ( cos(p/4) +i sin(p/4)) = 1+i
b. V�rifier que z1 est solution de l’�quation (2+i)z = 1+3i.
(2+i)(1+i) =2 +i +2i +i2 =2+3i-1=1+3i.
2. �crire le nombre complexe z2 = −1+i 3� sous forme exponentielle.
Module de z2 : (12 +3)� = 2.
z2 = 2 (-0,5 +i 3� /2) = 2(cos(2p/3 )+i sin (2p/3)) =2exp(i 2p/3).
3. On consid�re z3 le nombre complexe de module 4 et d’argument 7 p/6.
V�rifier que z3 = z21 �z2.
z21 =2 exp(ip/2) ; z2=2exp(i 2p/3).
z3 =4exp(i 2p/3+ip/2 )= 4 exp(i 7p/6)
4. Le plan complexe est muni d’un rep�re orthonorm�
On consid�re les trois points A, B et C d’affixes respectives zA = 1+i, zB = −1+i 3� et zC =−2 *3�−2i.
a. Placer les points A, B et C dans le plan complexe.

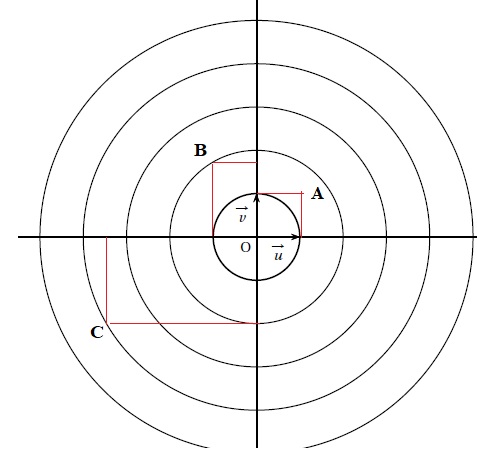
b. D�montrer que le triangle OBC est rectangle en O.
OB2 = (-1)2+(3�)2 =4.
OC2 = (-2*3�)2+(-2)2 =16.
zC-zB=−2 *3�−2i - (−1+i 3�)=(−2 *3�+1)-i (2+3�).
BC2 = (−2 *3�+1)2+(2+3�)2 =12 +1-4 *3�+4 +3 +4 *3�=20.
BC2 =OB2 +OC2 .
D'apr�s la r�ciproque du th�or�me de Pythagore, le triangle OBC est rectangle en O.


  

menu