Mathématiques,
bac STL biotechnologie Métropole septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. 5 points
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Les résultats seront arrondis à 10−2 près.
Une entreprise fabrique en grande quantité des boîtes de Petri destinées à des laboratoires d’analyses microbiologiques.
Dans cet exercice, on étudie la qualité de la production de ces boîtes.
Partie A.
L’entreprise affirme que la probabilité qu’une boîte ait un défaut est
égale à 0,03. On prélève au hasard 100 boîtes dans la production. La
production est assez importante pour que l’on puisse assimiler ce
prélèvement à un tirage aléatoire avec remise.
On désigne par X la variable aléatoire qui, à tout prélèvement de 100 boîtes, associe le nombre de boîtes présentant un défaut.
1. Justifier que la variable aléatoire X suit une loi binomiale et déterminer les paramètres de cette loi.
Il y a répétition de n =100 tirages indépendants et identiques. Chaque
tirage a deux issues : la boîte a un défaut p = 0,03 ; la boîte
est sans défaut 1-p = 0,97.
2. Déterminer la probabilité de l’évènement A : «Le prélèvement contient exactement 4 boîtes ayant un défaut ».
p(X=4) = (100 4) 0,034 x0,976=100 x99 x98 x97 /(2 x3 x4) x0,034 x0,9796~0,17.
3. Déterminer la probabilité de l’évènement B : « Le prélèvement contient au plus 3 boîtes ayant un défaut ».
P(B) =P(X=0) +P(X=1) +P(X=3) =0,0475 +0,147 +0,225 +0,227 ~0,65.
Partie B.
On désigne par Y la variable aléatoire qui, à une boîte de Petri prélevée au hasard, associe son diamètre en millimètre.
Le service qualité de l’entreprise estime que la variable aléatoire Y suit la loi normale d’espérance μ = 89,7 et d’écart type s = 0,20.
1. Déterminer la probabilité P(89,3 < Y < 90,1).
P(89,3 < Y ) = 0,02275 ; P(90,1 < Y ) = 0,9772 ; P(89,3 < Y < 90,1).=0,9772-0.02275 ~0,95.
2. Déterminer la probabilité qu’une boîte de Petri ait un diamètre supérieur ou égal à 89,9 mm.
P( Y > 89,9) = 1-P(89,9 < Y ) =1-0.841 ~0,16.
Partie C.
La machine de production a été réglée dans le but que 3% au maximum des
boîtes de Petri soient non conformes. On prélève un échantillon de 200
boîtes de Petri et on constate que parmi cellesci, 9 sont non conformes.
Suite à ce constat, doit -on accepter le réglage de cette machine ? Justifier.
1,96 (0,03 x0,97) / 100)½ =0,0334.
Intervalle de fluctuation :[0,03 -0,0334 ; 0,03 +0,0334] soit [-0,004 ; 0,063].
Fréquence observée : 9 /200 =0,045.
0,045 appartient à l'intervalle de fluctuation, la machine est bien réglée.
Exercice 2. 3 points.
Une
entreprise fabrique et commercialise des composants électroniques
destinés à fonctionner de manière continue. On a étudié la durée de
vie, en jour, de ces composants.
La variable aléatoire D associée à cette durée de vie suit une loi exponentielle de paramètre l = 0,0005.
On rappelle que P( D < t ) = 1−e− l¸t .
Pour chacune des affirmations suivantes, on précisera si elle est vraie
ou fausse en justifiant de manière claire et concise la réponse donnée.
Affirmation 1 : L’espérance de cette loi est égale à 2 000. Vrai.
µ = 1 / l = 1 / 0,0005 = 2000.
Affirmation 2 : La probabilité qu’un composant de ce type tombe en panne après les 500 premiers jours est environ 0,221. Faux.
P(D > 500) = e− l¸t =exp(-0,0005 x500) =0,7788.
Affirmation 3
: L’entreprise souhaite qu’au maximum 10% des composants tombent en
panne au cours de la période de garantie. Cette période de garantie
doit être d’environ 210 jours. Vrai.
P( D < t ) = 1−e− l¸t < 0,10 ; e− l¸t > 0,9 ; exp(-0,0005 t) > 0,9 ;
-0,0005 t > ln(0,9) ; -0,0005 t > -0,1054 ; t < 0,1054 / 0,0005 ; t < 211 jours.
|
...
|
|
Exercice 3 5 points
Dans un laboratoire d’industrie laitière, on cultive une population de
bactéries qui compte initialement 60 000 individus. On étudie
l’évolution du nombre de bactéries en fonction du temps.
Partie A.
On émet l’hypothèse que la population augmente de 18% toutes les heures
et on modélise l’évolution de cette population par une suite (un).
Pour tout entier naturel n, on note un le nombre de bactéries de la population étudiée après n heures. On a alors u0 = 60000.
1. Déterminer les termes u1 et u2.
u1 =60 000 x 1,18 =70 800 ; u2=70 800 x1,18 =83544.
2. Exprimer un+1 en fonction de un.
un+1 =1,18 un.
3. En déduire la nature de la suite (un).
Suite géométrique de raison 1,18 et de premier terme 60 000.
4. Exprimer alors un en fonction de n.
un = 60 000 x1,18n.
5. Déterminer u6 à l’unité près et interpréter ce résultat dans le contexte de l’exercice.
u6 = 60 000 x1,186 =161 973.
Nombre de bactéries au bout de 6 heures.
Partie B.
On souhaite déterminer à partir de combien d’heures la population de bactéries dépassera 200 000 individus.
Pour cela, on utilise un algorithme.
1. Recopier et compléter l’algorithme de sorte qu’à la fin de son exécution, la variable N contienne le nombre d’heures cherché.
N ←0
U ←60000
Tant queU < 200 000
N ←N +1
U ←U x 1,18
Fin Tant que.
2. Déterminer le nombre d’heures à partir duquel la population de bactéries dépassera 200 000.
Expliquer la démarche utilisée.
60 000 x1,18n> 200 000 ; 1,18n >10 /3 ; n log(1,18) > log(10 /3) ; n > 7,27 soit 8 heures.
|
....
|
Exercice 4.
7 points.
Des
scientifiques étudient la croissance d’une plante vivace d’une variété
donnée. Pour cela, ils ont relevé tous les mois la hauteur de plants
témoins, mesurant tous 12 cm au début de l’expérimentation.
Dans le tableau ci-dessous, h désigne la hauteur moyenne des plants, exprimée en centimètre, au bout de t mois.
t (mois)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
h( cm)
|
12
|
16,6
|
20
|
22
|
23,1
|
23,6
|
23,8
|
1. Construire le nuage de points correspondant au tableau ci-dessus.
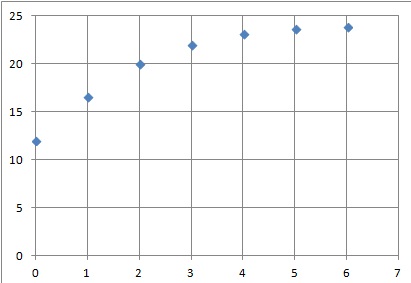
2. L’utilisation d’un ajustement affine du nuage de points semble-t-elle pertinente ?
Non, les points ne sont pas alignés.
3. On pose y = ln(24 / h -1)
Compléter la troisième ligne du tableau (arrondir les valeurs à 0,001 près)..
t (mois)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
h( cm)
|
12
|
16,6
|
20
|
22
|
23,1
|
23,6
|
23,8
|
y
|
0
|
-0,808
|
-1,609
|
-2,398
|
-3,245
|
-4,078
|
-4,779
|
4. On nomme D la droite d’ajustement de y en t obtenue par la méthode des moindres carrés.
L’équation réduite de D est de la forme y = at +b où a et b sont des
nombres réels. En utilisant la calculatrice, donner les valeurs de a et
b à 0,001 près.
y= -0,804 t -0,005.
5. On admet que h(t ) = 24 /(1 +e-0,8t).
Estimer, au centimètre près, la hauteur du plant au bout de 10 mois.
h(10) = 24 /(1+e-8) =23,99 ~24 cm.
6. Soit g la fonction définie sur l’intervalle [0 ; +∞[ par :
g (x) = 24 /(1+e-08x)
a. On note g ′ la fonction dérivée de la fonction g sur l’intervalle [0 ; +∞[ et on admet que :
g ′(x) =19,2 e−0,8x /(1+e-08x) .
En déduire les variations de la fonction g sur l’intervalle [0 ; +∞[.
Le terme en exponentielle est toujours positif ou nul.
g'(x) est positive ; g(x) est strictement croissante sur l’intervalle [0 ; +∞[.
b. Déterminer la limite de la fonction g en +∞puis interpréter graphiquement le résultat.
e-08x tend vers zéro quand x tend vers plus l'infini.
g(x) tend vers 24 quand x tend vers pus l'infini.
La droite d'équation y = 24 est asymptote à la courbe.
c. La taille de la plante pourra-t-elle atteindre 25 cm ? Justifier.
Non, la taille maximale des plantes est 24 cm.
|
|
