Mathématiques
bac S Amérique du sud 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
......
.....
|
Exercice 1.
6 points.
Les parties A, B et C peuvent être traitées de façon indépendante.
Dans tout l’exercice, les résultats seront arrondis à 10−3.
Le roller de vitesse est un sport qui consiste à parcourir une certaine
distance le plus rapidement possible en rollers. Dans le but de faire
des économies, un club de roller de vitesse s’intéresse à la gestion de
ses chronomètres et des roulements de ses rollers.
Partie A :
On note T la variable aléatoire égale à la durée de vie, en mois, d’un
chronomètre et on admet qu’elle suit une loi exponentielle de paramètre
l= 0,0555.
1. Calculer la durée de vie moyenne d’un chronomètre (arrondie à l’unité).
1 / l =1 / 0,0555 ~ 18 mois.
2. Calculer la probabilité qu’un chronomètre ait une durée de vie comprise entre un et deux ans.
P(T< 12)= 1 -exp(-12 x0,0555) =0,48624.
P(T< 24)= 1 -exp(-24x0,0555) =0,73605.
P(12 < T < 24) =0,73605-0.48624 ~0,250.
3. Un
entraîneur n’a pas changé son chronomètre depuis deux ans. Quelle est
la probabilité qu’il soit encore en état de fonctionner au moins un an
de plus ?
La loi exponentielle est à durée de vie sans vieillissement.
P T <24 (T > 36) = P(T> 12) =exp(-12 x0,0555) ~0,514.
Partie B :
Ce club fait des commandes groupées de roulements pour ses adhérents auprès de deux fournisseurs A et B.
— Le fournisseur A propose des tarifs plus élevés mais les roulements qu’il vend sont sans défaut avec une probabilité de 0,97.
— Le fournisseur B propose des tarifs plus avantageux mais ses roulements sont défectueux avec une probabilité de 0,05.
On choisit au hasard un roulement dans le stock du club et on considère les évènements :
A : « le roulement provient du fournisseur A »,
B : « le roulement provient du fournisseur B »,
D : « le roulement est défectueux ».
1. Le club achète 40% de ses roulements chez le fournisseur A et le reste chez le fournisseur B.
a. Calculer la probabilité que le roulement provienne du fournisseur A et soit défectueux.
P(A n D) =0,40 x 0,03 =0,012.
b. Le roulement est défectueux. Calculer la probabilité qu’il provienne du fournisseur B.
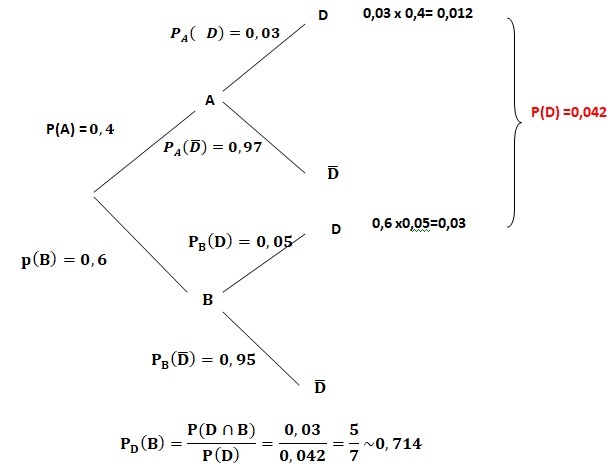
2. Si le club
souhaite que moins de 3,5% des roulements soient défectueux, quelle
proportion minimale de roulements doit-il commander au fournisseur A ?
Soit x la proportion de roulement issus de A : 0,03 x + 0,05(1-x) < 0,035 ;
-0,02 x +0,05 < 0,035 ; 0,02 x >0,015 ; x > 0,015 / 0,02 ; X > 0,75 ( 75 %).
Partie C :
Le diamètre intérieur standard d’un roulement sur une roue de roller est de 8 mm.
On note X la variable aléatoire donnant en mm le diamètre d’un
roulement et on admet que X suit une loi normale d’espérance 8 et
d’écart type 0,1.
Un roulement est dit conforme si son diamètre est compris entre 7,8 mm et 8,2 mm.
1. Calculer la probabilité qu’un roulement soit conforme.
P ( X > 7,8) =0,9773 ; P ( X > 8,2) =0,02275 ;
P( 7,8 < X < 8,2 )=0,9775 -0,02275~0,954.
2. Le fournisseur B vend ses roulements par lots de 16 et affirme que seulement 5% de ses roulements sont non conformes.
Le président du club, qui lui a acheté 30 lots, constate que 38 roulements sont non conformes.
Ce contrôle remet-il en cause l’affirmation du fournisseur B ?
On pourra utiliser un intervalle de fluctuation asymptotique au seuil de 95%.
1,96 (0,05 x0,95 / (30 x16))½ =0,0195.
Intervalle de fluctuation : [ 0,05 -0,0195 ; 0,05 +0,0195 ] soit [0,0305 ; 0,0695].
Fréquence observée : f = 38 / (30 x16) ~0,0792.
Cette fréquence n'appartient pas à l'intervalle précédent. L'affirmation du fournisseur est remise en cause.
3. Le fabricant de roulements de ce fournisseur décide d’améliorer la production de ses roulements.
Le réglage de la machine qui les fabrique est modifié de sorte que 96%
des roulements soient conformes. On suppose qu’après réglage la
variable aléatoire X suit une loi normale d’espérance 8 et d’écart-type
s.
a. Quelle est la loi suivie par (X −8) / s ?
Loi normale centrée réduite( 0 ; 1).
b. Déterminer s pour que le roulement fabriqué soit conforme avec une probabilité égale à 0,96.
P(7,8 < X < 8,2) = 0,96 ; P(7,8 -8 < X-8 < 8,2-8) = 0,96 ; P(-0,2 < X-8 < 0,2) = 0,96 ; P(-0,2/ s < (X-8) / s < 0,2 / s) = 0,96 ;
P(-0,2/ s < (Z < 0,2 / s) = 0,96 ; 2P(Z < 0,2 / s)-1 = 0,96 ; P(Z < 0,2 / s) =0,98 ; 0,2 / s = 2,054.
s = 0,097.
|
...
|
|
Exercice 2. 5 points.
La vasopressine est une hormone favorisant la réabsorption de l’eau par l’organisme.
Le taux de vasopressine dans le sang est considéré normal s’il est inférieur à 2,5 μg/mL.
Cette hormone est sécrétée dès que le volume sanguin diminue. En
particulier, il y a production de vasopressine suite à une hémorragie.
On utilisera dans la suite la modélisation suivante :
f (t ) = 3te-0,25t +2 avec t >0,
où f (t ) représente le taux de vasopressine (en μg/mL) dans le sang en
fonction du temps t (en minute) écoulé après le début d’une hémorragie.
1. a. Quel est le taux de vasopressine dans le sang à l’instant t = 0 ?
f(0) = 2 µg / mL.
b. Justifier que douze secondes après une hémorragie, le taux de vasopressine dans le sang n’est pas normal.
12 s ou 12 / 60 = 0,2 minute.
f(0,2) = 3 x0,2 exp(-0,25 x0,2) +2 = 2,57 µg / mL, valeur supérieure à 2,5 µg / mL.
c. Déterminer la limite de la fonction f en +∞. Interpréter ce résultat.
Le terme en exponentielle tend vers zéro si t tend vers plus l'infini.
3te-0,25t tend vers zéro et f(t) tend vers 2.
Au bout d'un temps suffisamment long le taux de vasopresine dans le sang tend vers 2 µg / mL.
2. On admet que la fonction f est dérivable sur [0 ; +∞[.
Vérifier que pour tout nombre réel t positif,
f ′(t )=0,75 (4-t) e-0,25t .
On pose u = 3t et v = e-0,25t ; u' = 3 et v' = -0,25 e-0,25t ;
u'v + v' u = 3e-0,25t -0,75t e-0,25t = (3-0,75 t)e-0,25t =0,75 (4-t) e-0,25t .
3. a. Étudier le sens de
variation de f sur l’intervalle [0 ; +∞[ et dresser le tableau de
variations de la fonction f (en incluant la limite en +∞).
e-0,25t est positif ; le signe de f '(t) est celui de 4-t.
Si t < 4, f '(t) est positive et f(t) est croissante.
Si t >4, f '(t) est négative et f(t) est décroissante.
Si t = 4, f '(t) est nulle est f(t) présente un maximum.
b. À quel instant le taux de vasopressine est-il maximal ?
Quel est alors ce taux ? On en donnera une valeur approchée à 10−2 près.
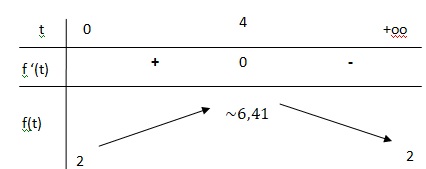
4. a. Démontrer qu’il existe une unique valeur t0 appartenant à [0; 4] telle que f (t0) = 2,5.
En donner une valeur approchée à 10−3 près.
Sur cet intervalle, f(t) est continue ( car dérivable) et strictement croissante ; f(0) = 2 et f(4) ~6,41 µg / mL.
D'après le théorème de la bijection, l'équation f(t0) = 2,5 admet une unique solution sur cet intervalle.
t0 ~0,174 minute.
On admet qu’il existe une unique valeur t1 appartenant à [4 ; +∞[ vérifiant f (t1) = 2,5.
On donne une valeur approchée de t1 à 10−3 près : t1 ≈ 18,930.
b. Déterminer
pendant combien de temps, chez une personne victime d’une hémorragie,
le taux de vasopressine reste supérieur à 2,5 μg/mL dans le sang.
t1-t0 = 18,930 -0,174 ~18,756 minutes.
5. Soit F la fonction définie sur [0 ; +∞[ par F(t ) = −12(t +4)e−0,25t +2t .
a. Démontrer que la fonction F est une primitive de la fonction f et en déduire une valeur approchée de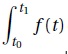 à l’unité près. à l’unité près.
On pose u = t+4 et v = e-0,25t ; u' = 1 et v' = -0,25 e-0,25t ;
u'v + v' u = e-0,25t -0,25(t+4) e-0,25t = -0,25 t e-0,25t .
F'(t) = 12 x0,25 t e-0,25t +2 = 3t e-0,25t +2 = f(t).
b. En déduire une
valeur approchée à 0,1 près du taux moyen de vasopressine, lors d’un
accident hémorragique durant la période où ce taux est supérieur à 2,5
μg/mL.
(F(t1-F(t0) ) / (t1-t0).
F(18,93)= -12x22,93 exp(-0,25 x18,93) +2 x18,93 ~35,43.
F(0,174)= -12x4,174 exp(-0,25 x0,174) +2 x0,174 ~-47,608.
(35,43 -(- 47,608)) / 18,756 ~4,4 µg / mL.
|
....
|
Exercice 3. 4 points
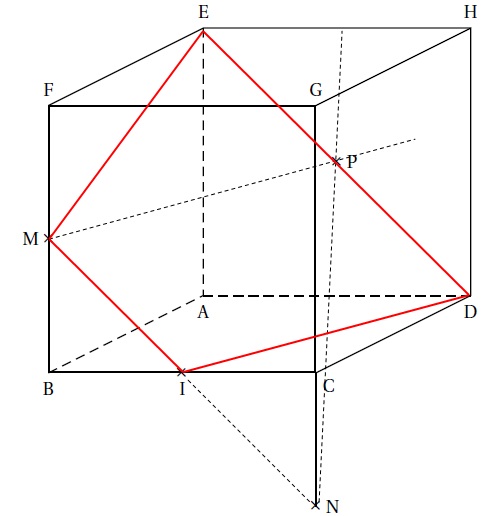
On considère un cube ABCDEFGH.
Le point M est le milieu de [BF], I est lemilieu de [BC], le point N est défini par la relation suivante.
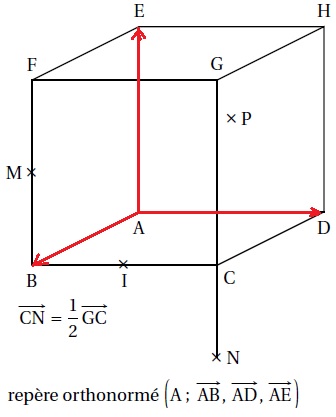
Le point P est le centre de la face ADHE.
Partie A :
1. Justifier que la droite (MN) coupe le segment [BC] en son milieu I.
Soit K le point d'intersection de la droite (MN) et du segment [BC].
Les droites (BM) et (CN) sont parallèles ; les droites (BC) et (MN) sont deux sécantes.
Les triangles rectangles BMK et CNK sont semblables :
BK / KC =BM / CN = 1.
Donc K est le milieu du segment [BC] ; K est confondu avec I.
2. Construire la section du cube par le plan (MNP).
Les points M et I appartiennent à la fois au plan (MNP) et au plan
(BCGF) face avant du cube. [MI] est l'intersection de ces deux plans.
D(0 ; 1 ;0) appartient au plan (MNP) d'équation x +2y+2z -2 = 0 ( voir ci-dessous ).
Les points D et I appartiennent à la fois au plan (MNP) et au plan
(ABCD) base du cube. [DI] est l'intersection de ces deux plans.
E(0 ; 0 ;1) appartient au plan (MNP) d'équation x +2y+2z -2 = 0 ( voir ci-dessous ).
Les points D et E appartiennent à la fois au plan (MNP) et au plan
(ADEH) face arrière du cube. [DE] est l'intersection de ces deux plans.
Les points M et E appartiennent à la fois au plan (MNP) et au plan (ABFE). [ME] est l'intersection de ces deux plans.
Partie B :
1. Justifier que le vecteur 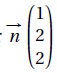 est un vecteur normal au plan (MNP).
est un vecteur normal au plan (MNP).
En déduire une équation cartésienne du plan (MNP).
M( 1 ; 0 ; ½) ; N( 1 ; 1 ; -½) ; P( 0 ; ½ ; ½ ).

Equation cartésienne du plan (MNP) :
x +2y+2z +d = 0.
M appartient à ce plan : 1+1+d = 0 ; d = -2.
x +2y+2z -2 = 0.
2. Déterminer un système d’équations paramétriques de la droite (d) passant par G et orthogonale au plan (MNP).
Le vecteur 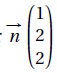 est un vecteur directeur de la droite (d).
est un vecteur directeur de la droite (d).
x = t +xG = t+1 ; y = 2 t +yG = 2t +1 ; z = 2t +zG = 2t +1 avec t réel.
3. Montrer que la droite (d) coupe le plan (MNP) au point K de coordonnées (2 /3 ; 1 / 3 ; 1 / 3).
K appartient à la droite (d) : xK = t+1 ; yK = 2t+1 ; zK = 2t+1.
K appartient au plan (MNP) : t+1 +4t+2 +4t+2 -2 = 0 ; 9t +3 = 0 ; t = -1 /3.
xK = t+1 =2 / 3 ; yK = 2t+1 = 1 / 3 ; zK = 2t+1= 1 /3.
En déduire la distance GK.
GK = [(1-2 /3) 2 +(1-1 /3)2 +(1-1/3)2]½ =(1 / 9 + 4 /9 +4 / 9)½ = 1
4. On admet que les quatre points M, E, D et I sont coplanaires et que l’aire du quadrilatère MEDI est 9 / 8 unités d’aire.
Calculer le volume de la pyramide GMEDI.
V = aire de base fois hauteur / 3 = aire de base x GK / 3 = 9 / 8 x1 / 3 = 3 / 8 unité de volume.
|
Exercice 4.
On considère la suite (un) définie pour tout entier n >0 par : un+1 = 3-10 / (un+4) et
u0 = 5.
Partie A :
1. Déterminer la valeur exacte de u1 et de u2.
u1 = 3-10 / (u0+4) = 3-10 / 9 =(27-10) / 9 = 17 / 9.
u2 = 3-10 / (u1+4) = 3-10 / (17 / 9 +4) =3-90 / 53 =(159-90) / 53 = 69 / 53.
2. Démontrer par récurrence que pour tout entier naturel n, un >1.
Initialisation : u1 =17 / 9.La relation est vraie au rang 1.
Hérédité : On suppose que up >1 est vraie
up+1 = 3-10 / (up+4) avec up+4 > 5.
1 / (up+4) < 1 / 5 ; 10 / (up+4) < 10 / 5 ; 10 / (up+4) < 2 ;
-10 / (up+4) > -2 ;
3-10 / (up+4) > 3-2 ; 3-10 / (up+4) > 1 ; up+1 >1, la propriété est vraie au rang p+1.
Conclusion : la propriété étant vraie au rang 1 et héréditaire, elle est vraie pout tout entier naturel.
3. Démontrer que, pour tout entier nature n, un+1 −un =(1−un ) (un +2) / ( un +4).
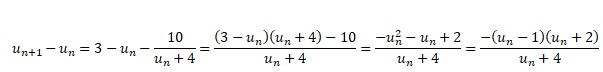
4. En déduire le sens de variation de la suite (un).
un > 1 ; (un +2) et ( un +4) sont positifs ; (1−un ) est négatif ou nul.
un+1 −un < 0. La suite est décroissante.
5. Justifier que la suite (un) converge.
La suite est décroissante et minorée ( un > 1), donc elle converge.
Partie B :
On considère la suite (vn) définie pour tout entier naturel n par vn =(un-1) / (un+2).
1. a. Démontrer que (vn) est une suite géométrique dont on déterminera la raison et le premier terme v0.
vn+1 =(un+1-1) / (un+1+2).
un+1 = 3-10 / (un+4).
un+1-1 = 2-10 / (un+4) =(2un-2) / (un+4).
un+1+2=5-10 / (un+4) =(5un+10) / (un+4).
vn+1 =(2un-2) / (5un+10) =2 / 5 vn.
(vn) est une suite géométrique de raison 2 /5 = 0,4 et de premier terme v0 = (u0-1) / (u0+2)=4 / 7.
b. Exprimer vn en fonction de n.
En déduire que pour tout entier naturel n, vn diffère de 1.
vn =v0 x 0,4n=4 / 7x 0,4n.
4 / 7 diffère de 1 ; 0,4n est inférieur ou égal à 1 ; donc vn diffère de 1.
2. Démontrer que pour tout entier naturel n, un =(2vn +1) / (1−vn).
vn =(un-1) / (un+2)=4 / 7x 0,4n.
vn(un+2)=un-1 ; vn un+2vn=un-1 ; un ( 1-vn) = 1+2vn ; un =(2vn +1) / (1−vn).
3. En déduire la limite de la suite (un).
un =(8 / 7x 0,4n +1) / (1−4 / 7x 0,4n).
Quand n tend vers plus l'infini : 0,4n tend vers zéro.
1−4 / 7x 0,4n tend vers 1 et 8 / 7x 0,4n +1 tend vers 1.
La limite de cette suite (un) est égale à 1.
Partie C :
On considère l’algorithme ci-dessous.
1. Après exécution de l’algorithme, quelle valeur est contenue dans la variable n ?
2. À l’aide des parties A et B, interpréter cette valeur.
u←5
n←0
Tant que u >1,01
n←n +1
u←3− 10 /(u +4)
Fin du Tant que
L'algorithme s'arrète dès que u <1,01.
u5 =(8 / 7x 0,45 +1) / (1−4 / 7x 0,45)~1,0176.
u6 =(8 / 7x 0,46 +1) / (1−4 / 7x 0,46)~1,0073.
n est égal à 6.
La suite (un) est décroissante e converge vers1.
L'algorithme affiche la première valeur de n pour laquelle un <1,01.
|
|
|