Mathématiques, Brevet Métropole, Antilles, La Réunion septembre 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . ( 18 points )
Michel participe à un rallye VIT sur un parcours balisé. Le trajet est représenté en traits pleins. Le départ du rallye est en A et l’arrivée est en G.

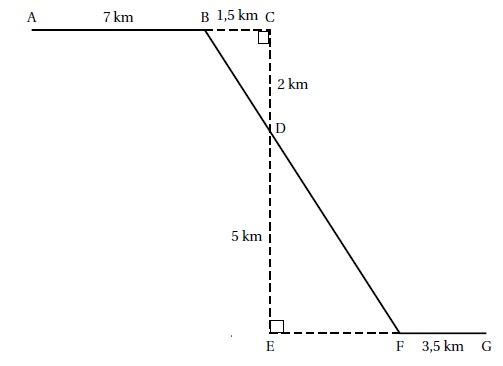
1. Montrer que la longueur BD est égale à 2,5 km.
Relation de Pythagore dans le triangle rectangle BCD : BD² = 1,5² +2² =6,25 : BD =2,5 km.
2. Justifier que les droites (BC) et (EF) sont parallèles.
Les droites (BC) et (EF) sont perpendiculaires à la droite (CE). Les droites (BC) et (EF) sont parallèles.
3. Calculer la longueur DF.
DF / BD =DE / CD ; DF / 2,5 =5 / 2 = 2,5 ; DF = 2,5 x2,5 =6,25 km.
4. Calculer la longueur totale du parcours.
AB +BD +DF +FG =7 +2,5 +6,25 +3,5 =19,25 km.
5. Michel roule à une vitesse moyenne de 16 km/h pour aller du point A au point B.
Combien de temps mettra-t-il pour aller du point A au point B?
Donner votre réponse en minutes et secondes.
7 /16 = 0,4375 heure ou 0,4375 x60 = 26,25 minutes ou 26 min 15 s.

Exercice 2 ( 14 points).
1. a. Déterminer la décomposition en produit de facteurs premiers de 2 744.
2744 = 2³ x 7³.
b. En déduire la décomposition en produit de facteurs premiers de 2744².
2744² = 2⁶ x 7⁶.
c. À l’aide de cette décomposition, trouver x tel que x³ = 2744².
2744² = (2² x 7²)³ ; x = (2 x7) ² = 196.
2. Soient a et b deux nombres entiers supérieurs à 2 tels que a³ = b².
a. Calculer b lorsque a = 100.
b² = 100³ = 10^2x3 =(10³)² ; b = 1000.
b. Déterminer deux nombres entiers a et b supérieurs à 2 et inférieurs à 10 qui vérifient l’égalité a³ = b².
b = 8 et a =4.

Exercice 3 (17 points).
Les activités humaines produisent du dioxyde de carbone (CO₂) qui contribue au réchauffement climatique.
Le graphique suivant représente l’évolution de la concentration atmosphérique moyenne en CO₂ (en ppm) en fonction du temps (en année).

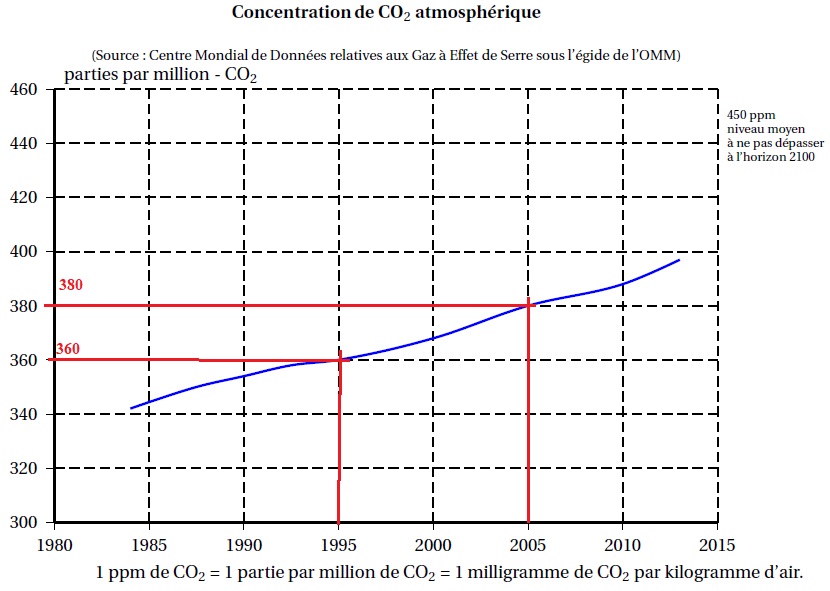
1. Déterminer graphiquement la concentration de CO₂ en ppm en 1995 puis en 2005.
2. On veut modéliser l’évolution de la concentration de CO₂ en fonction du temps à l’aide d’une fonction g où g (x) est la concentration de CO₂ en ppm en fonction de l’année x.
a. Expliquer pourquoi une fonction affine semble appropriée pour modéliser la concentration en CO₂ en fonction du temps entre 1995 et 2005.
Tous les points de la courbe bleue sont à peu près alignés entre 1995 et 2005..
b. Arnold et Billy proposent chacun une expression pour la fonction g :
Arnold propose l’expression g (x)= 2x −3630 ;
Billy propose l’expression g (x)= 2x −2000.
Quelle expression modélise le mieux l’évolution de la concentration de CO₂ ? Justifier.
2 x1995 -3630 =360 ; 2 x2005-3630 =380.
L’expression g (x)= 2x −3630 convient.
c. En utilisant la fonction que vous avez choisie à la question précédente, indiquer l’année pour laquelle la valeur de 450 ppm est atteinte.
450 = 2x-3630 ; 2x = 3630+450 =4080 ; x = 2040.
3. En France, les forêts, grâce à la photosynthèse, captent environ 70 mégatonnes de CO₂ par an, ce qui représente 15% des émissions nationales de carbone (année 2016). Calculer une valeur approchée à une mégatonne près de la masse M du CO2 émis en France en 2016.
70 / 0,15 ~ 467 mégatonnes.

Exercice 4. ( 16 points).
Pour le mariage de Dominique et Camille, le pâtissier propose deux pièces montées constituées de gâteaux de tailles et de formes différentes.
La tour de Pise :
La première pièce montée est constituée d’un empilement de 4 gâteaux de forme cylindrique, de même hauteur et dont le diamètre diminue de 8 cm à chaque étage. Le gâteau du bas a pour diamètre 30 cm et pour hauteur 6 cm.
La tour Carrée :
La deuxième pièce montée est constituée d’un empilement de 3 pavés droits à base carrée de même hauteur. La longueur du côté de la base diminue de 8 cm à chaque étage.
La hauteur des gâteaux est 8 cm ; le côté de la base du gâteau du bas mesure 24 cm.

Tous les gâteaux ont été confectionnés à partir de la recette ci-dessous qui donne la quantité des ingrédients correspondant à 100 g de chocolat.
65 g de sucre ; 2 oeufs ; 75 g de beurre : 30 g de farine.
1. Quel est le ratio (masse de beurre : masse de chocolat) ? Donner le résultat sous forme de fraction irréductible.
75 / 100 = 3 / 4 .
2. Calculer la quantité de farine nécessaire pour 250 g de chocolat noir suivant la recette ci-dessus.
30 x250 / 100 = 75 g.
3. Calculer la longueur du côté de la base du plus petit gâteau de la tour Carrée.
Etage n°1 : 24 cm ; étage n°2 : 24 -8 = 16 cm ; étahe n°3 : 16 -8 = 8 cm.
4. Quelle est la tour qui a le plus grand volume ? Justifier votre réponse en détaillant les calculs.
La tour de Pise : étage n°1 : 3,14 x15² x6 =4241 cm³.
Etage n°2 : 3,14 x11² x6 =2281 cm³.
Etage n°3 : 3,14 x7² x6 =924 cm³.
Etage n°4 : 3,14 x3² x6 =170 cm³.
Volume total : 7616 cm³.
La tour Carrée : étage n°1 : 24² x8 =4608 cm³.
Etage n°2 : 16² x8 =2048 cm³.
Etage n°3 : 8² x8 =512 cm³
Volume total : 7168 cm³.
La tour de Pise a le plus grand volume.

Exercice 5. ( 15 points).
On donne le programme de calcul suivant :
Étape 1 : Choisir un nombre de départ
Étape 2 : Ajouter 6 au nombre de départ
Étape 3 : Retrancher 5 au nombre de départ
Étape 4 : Multiplier les résultats des étapes 2 et 3
Étape 5 : Ajouter 30 à ce produit
Étape 6 : Donner le résultat
1. a. Montrer que si le nombre choisi est 4, le résultat est 20.
4 +6 = 10 ; 4-5 = -1 ; 10 x(-1) = -10 ; -10 +30=20.
b. Quel est le résultat quand on applique ce programme de calcul au nombre −3 ?
-3+6 = 3 ; -3 -5 = -8 ; -8 x3 = -24 ; -24 +30 = 6.
2. Zoé pense qu’un nombre de départ étant choisi, le résultat est égal à la somme de ce nombre et de son carré.
a. Vérifier qu’elle a raison quand le nombre choisi au départ vaut 4, et aussi quand on choisit −3.
4² +4 = 20 ; (-3)² -3 = 6.
b. Ismaël décide d’utiliser un tableur pour vérifier l’affirmation de Zoé sur quelques exemples.

B6			=B1+B1^2
	A	B	C	D	E	F
1	étape1	2	5	7	10	20
2	étape 2	8	11	13	16	26
3	étape 3	-3	0	2	5	15
4	étape4	-24	0	26	80	390
5	résultat	6	30	56	110	420
6	somme du nombre et de son carré	6	30	56	110	420

Il a écrit des formules en B2 et B3 pour exécuter automatiquement les étapes 2 et 3 du programme de calcul.
Quelle formule à recopier vers la droite a-t-il écrite dans la cellule B4 pour exécuter l’étape 4 ?
=B2*B3
c. Zoé observe les résultats, puis confirme que pour tout nombre x choisi, le résultat du programme de calcul est bien x² +x. Démontrer sa réponse.
(x+6) (x-5)+30 = x²+6x-5x-30 +30 =x² +x.
d. Déterminer tous les nombres pour lesquels le résultat du programme est 0.
x²+x=x(x+1)=0 ; x=0 et x = -1.

Exercice 6. 17 points.
Deux amis Armelle et Basile jouent aux dés en utilisant des dés bien équilibrés mais dont les faces ont été modifiées. Armelle joue avec le dé A et Basile joue avec le dé B. Lors d’une partie, chaque joueur lance son dé et celui qui obtient le plus grand numéro gagne un point.
Voici les patrons des deux dés :

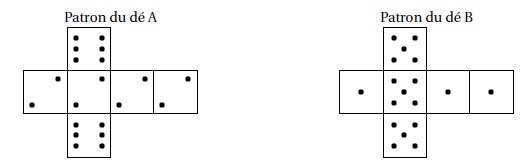
1. Une partie peut-elle aboutir à un match nul ? Non.
2. a. Si le résultat obtenu avec le dé A est 2, quelle est la probabilité que Basile gagne un point ?
3 cas favorables ( 5) sur 6 possibles . Probabilité de gagné : 0,5.
b. Si le résultat obtenu avec le dé B est 1, quelle est la probabilité qu’Armelle gagne un point ?
6 cas favorables sur 6 possibles. La probabilité du gain est égale à 1.
3. Les joueurs souhaitent comparer leur chance de gagner. Ils décident de simuler un match de soixante mille duels à l’aide d’un programme informatique.
Voici une partie du programme qu’ils ont réalisé.

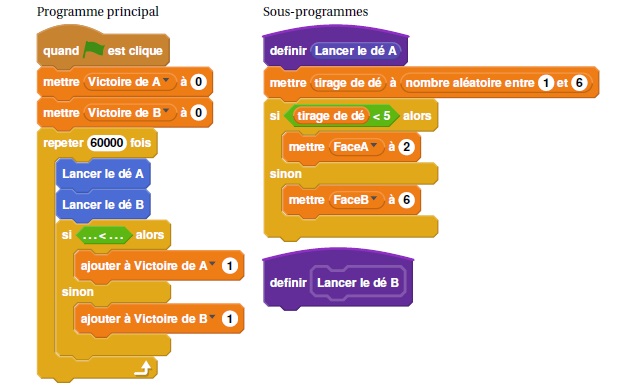
On précise que l’expression (nombre aléatoire entre 1 et 6) renvoie de manière équiprobable un nombre pouvant être 1; 2; 3; 4; 5 ou 6.
Les variables FaceA et FaceB enregistrent les résultats des dés A et B. Par exemple, la variable FaceA peut prendre soit la valeur 2 soit la valeur 6, puisque ce sont les seuls nombres présents sur le dé A.
Les variables Victoire de A et Victoire de B comptent les victoires des joueurs.
1. Lorsqu’on exécute le sous-programme « Lancer le dé A », quelle est la probabilité que la variable FaceA prenne la valeur 2 ?
4 cas favorables (1 ; 2 ; 3 ; 4 ) sur 6 possibles. La probabilité est égale à 4 /6 = 2 /3.
2. Recopier la ligne 7 du programme principal en la complétant.
si FaceB < FaceA alors
3. Rédiger un sous-programme « Lancer le dé B » qui simule le lancer du dé B et enregistre le nombre obtenu dans la variable FaceB.
mettre tirage de dé à nombre aléatoire entre 1 et 6
si tirage de dé < 2 alors
mettre FaceA à 1
sinon
mettre faceA à5
Après exécution du programme principal, on obtient les résultats suivants :
Victoire de A= 39901 Victoire de A= 20099
1. Calculer la fréquence de gain du joueur A, exprimée en pourcentage. On donnera une valeur approchée à 1% près.
39901 / 60000 ~0,67 (67 %).
2. Conjecturer la probabilité que A gagne contre B.
A gagne en moyenne 2 fois sur 3.