Math�matiques,  Groupe C Bts 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. . . ...... ..... Exercice 1. 10 points. Partie A : mod�lisation. On s’int�resse � la chute d’un parachutiste, avant l’ouverture du parachute. On admet que la vitesse V du parachutiste pendant la chute peut �tre mod�lis�e par une fonction solution de l’�quation diff�rentielle : my′(t )+ky(t ) =mg o� m est la masse totale du parachutiste et de son parachute, k est un coefficient d�pendant de la r�sistance de l’air, g est le coefficient de l’acc�l�ration de la pesanteur et t repr�sente le temps. V est exprim�e en m.s−1, m est exprim�e en kilogramme et t est exprim� en seconde. Dans la suite du probl�me, on consid�re que m = 80 kg, k = 25 unit�s S. I. et g = 10m.s−2. Au d�but de la chute, t = 0 s et V (0) = 0 ms−1. 1. Montrer que la fonction V est solution de l’�quation diff�rentielle (E) : y′ +0,3125y = 10. 80 y' +25 y =80 x10 = 800 ; y' +25 /80 = 800 /80 ; y' +0,3125 y = 10. 2. R�soudre l’�quation diff�rentielle : (E0) : y′+0,3125y = 0. V = A e-0,3125t avec A une constante. 3. D�terminer une fonction constante solution de (E). V = 10 /0,3125 = 32. 4. En d�duire les solutions g�n�rales de (E). V = 32 + Ae-0,3125t.  D�terminer une expression de la vitesse V (t ) du parachutiste � l’instant t . V(0) = 0 ; 0 = 32 +A ; A = -32 ; V(t) = 32 ( 1-e-0,3125t). Partie B : �tude de la chute. On admet que la vitesse du parachutiste est mod�lis�e par la fonction V de la variable t d�finie sur [0 ; +∞[ par : V(t) = 32 ( 1-e-0,3125t). On donne ci-dessous la repr�sentation graphique  de cette fonction V dans un rep�re orthogonal. 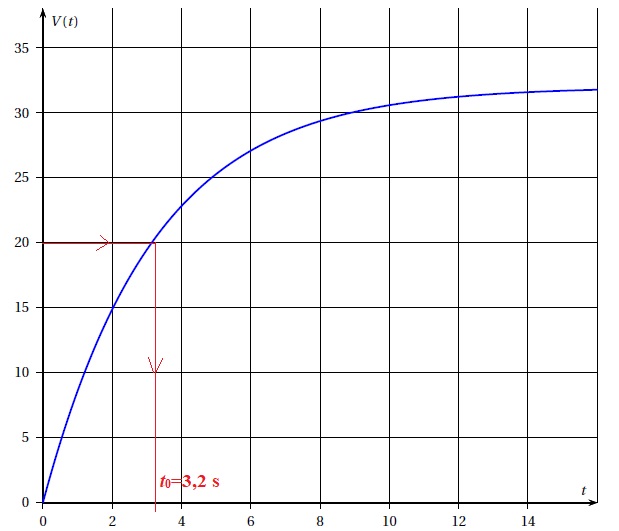1. a. Estimer une valeur arrondie de l’instant t0 � partir duquel la vitesse d�passe 20m.s−1. b. Retrouver par le calcul la valeur exacte de t0. 32 ( 1-e-0,3125t) > 20 ; 1-e-0,3125t) > 20 /32 ; 1-e-0,3125t > 0,625. e-0,3125t < 1-0,625 ; e-0,3125t < 0,375 ; -0,3125t0 > ln(0,375) ; t0 > 3,14 s. Un logiciel de calcul formel donne le r�sultat suivant que l’on admet et qui pourra �tre exploit� dans les questions suivantes. La limite de V(t) en plus l'infini est �gale � 32. 2. a. Donner l’expression V ′(t ) de la d�riv�e de la vitesse. V'(t) = 32 x0,3125e-0,3125t =10e-0,3125t. b. �tudier le sens de variations de V sur [0 ; +∞[. V'(t) est strictement positive ; V(t) est strictement croissante sur [0 ; +∞[. 3. Le parachutiste peut-il atteindre une vitesse de 130 km.h−1 ? 130 / 3,6 = 36,1 m /s, valeur sup�rieure � la vitesse limite 32 m /s. Il ne peut pas atteindre cette vitesse. 4. Calculer la vitesse moyenne du parachutiste lors des deux premi�res secondes de chute. On pourra arrondir � l’unit�. ... 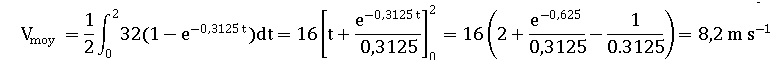Exercice 2. 10 points.. Une fonderie fabrique en grande quantit� des poutrelles m�talliques de type IPE 120. On donne ci-dessous le sch�ma de coupe d’une poutrelle de ce type. 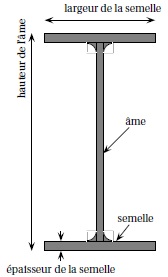Les dimensions, en millim�tre, d’une poutrelle de ce type sont : • hauteur de l’�me : 120 mm • largeur de la semelle : 64 mm • �paisseur de l’�me : 4,4mm • �paisseur de la semelle : 6,3mm Les trois parties de cet exercice sont ind�pendantes. Partie A : dimensions externes. Lors d’un contr�le de qualit� on constate que : • la hauteur de l’�me est conforme pour 98% des poutrelles ; • lorsque la hauteur de l’�me est conforme, la largeur de la semelle est �galement conforme dans 99% des cas. On choisit une poutrelle au hasard dans la production et on consid�re les �v�nements suivants : H : � la hauteur de l’�me est conforme � L : � la largeur de la semelle est conforme �. 1. Repr�senter la situation � l’aide d’un arbre pond�r�. 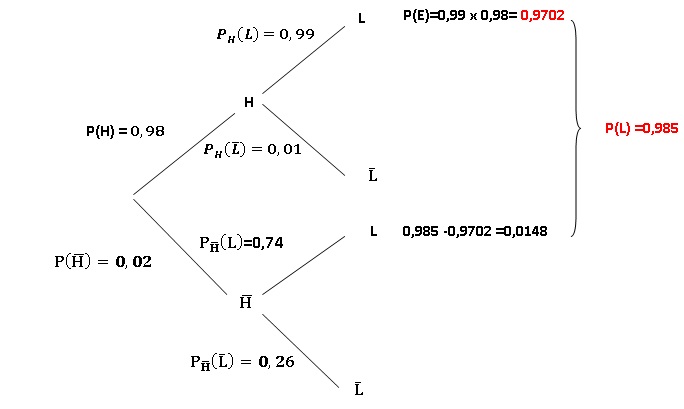2. On dit que les dimensions externes d’une poutrelle sont conformes lorsque la hauteur de l’�me et la largeur de la semelle sont conformes. On note E cet �v�nement. Justifier que p(E)= 0,9702. 3. Sachant que la largeur de la semelle est conforme pour 98,5% des poutrelles, l’affirmation suivante est-elle exacte ? La r�ponse devra �tre justifi�e par un calcul. � 26% des poutrelles dont la hauteur d’�me est non conforme pr�sentent �galement un d�faut de largeur de la semelle. � 4. On pr�l�ve au hasard 20 poutrelles. La production est suffisamment importante pour assimiler ce pr�l�vement � des tirages avec remise. On note N la variable al�atoire qui, � chaque lot de 20 poutrelles pr�lev�es au hasard, associe le nombre de poutrelles dont les dimensions externes sont conformes. a. D�terminer en justifiant la loi de probabilit� de la variable al�atoire N et pr�ciser ses param�tres. Les pr�levements sont ind�pendants et leur nombre est fix� � n = 20.  Chaque tirage peut d�boucher seulement sur 2 r�sultats  : la probabilit� qu'une poutrelle soit conforme est constante p = 0,9702. La probabilit� qu'une ppotrelle ne soit pas en conforme est q = 1-p = 0,0298. La loi binomiale B(n=20, p = 0,9702) est valide b. Calculer la probabilit� qu’un lot de 20 poutrelles contienne au moins une poutrelle dont les dimensions externes sont non conformes. Arrondir le r�sulta! � 10−3. Probabilit� que les 20 poutrelles soient conformes : P(N=20) = 0,546. Probabilit� qu'il y ait au moins une poutrelle non conforme : 1-P(N=20)=1-0,546 =0,454. .... Partie B. Epaisseur de l'�me. La variable al�atoire X qui, � chaque poutrelle associe l'�paisseur de l'�me ( en mm ) suit la loi normale d'esp�rance m = 4,4 et d'�cart type s = 0,02. l'�paisseur de l'�me est conforme si l'�cart entre la valeur r�elle et la valeur th�orique (4,4 mm) est inf�rieure ou �gal � 1 % de la valeur th�orique. Calculer la probabilit� qu'une poutrelle pr�lev�e au hasard, ait une �paisseur d'�me conforme. L'�paisseur doit �tre comprise entre 4,4 x0,99 = 4,356 et 4,4 x1,01 =4,444. P(X < 4,356) =0,0139. P(X < 4,444) =0,9861. P(4,356 < X < 4,356) =0,9861 -0,0139= 0,972. Partie C. Contr�le de conformit�. Une scie d�bite de longues poutrelle en tron�ons de longueur 2 m. L est la variable al�atoire, qui � chaque poutrelle d�bit�e, associe sa longueur ( en m�tre ). Si la scie est correctement r�gl�e, L suit la loi normale d'esp�rance � =2 et d�cart type s = 0,001. Pour le v�rifier, un technicien pr�l�ve un �chantillon de 100 poutrelles et a obtenu une valeur moyenne �gale � 1,9997 m. Lmoy est la variable al�atoire qui, � chaque �chantillon de 100 poutrelles, associe la longueur moyenne des poutrelles. Lmoy suit la loi normale d'esp�rance � et d'�cart type s0 = s / 10 quand la scie est bien r�gl�e. Le technicien construit un test bilat�ral au seuil de 5 % pour tester l'hypoth�se H0 " la longieur moyenne en m�tre est m = 2". 1. Donner l'hypoth�se alternative H1. La longueur moyenne diff�re de 2 m. 2. D�terminer l'intervalle I = [2-h ; 2+h], tel que, sous l'hypoth�se H0, P(Lmoy appartient � I) = 0,95. L'intervalle de fluctuation au seuil de 5 % est [2-1,96 s0 ; 2 +1,96 s0] soit {1,9998 ; 2,0002 ]. 3. Au seuil de d�cision de 5 %, la scie est-elle bien r�gl�e ? 1,9997 n'appartient pas � cet intervalle. L'hypoth�se H0 est rejet�e. La scie n'est pas correctement r�gl�e.   .

menu