Mathématiques,
Groupe D Bts 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1.
10 points.
Staphylococcus
Aurerus (SA), plus communément appelé staphylocoque doré, est une
bactérie responsable de nombreuses intoxications alimentaires. Elle est
naturellement présente chez l’homme.
Déposée sur un aliment et sous certaines conditions (comme notamment la
présence suffisante de
nutriments), elle se développe très fortement et produit des toxines.
Ces toxines, une fois ingérées,
sont responsables de troubles alimentaires, qui peuvent aller, dans
certains cas extrêmes, jusqu’à la
mort de la personne touchée.
Partie A : Équation différentielle.
1. Déterminer les solutions sur l’intervalle [0 ; +∞[ de l’équation différentielle
20y′ −20,8y = 0
où y est une fonction de la variable réelle t , définie et dérivable sur l’intervalle [0 ; +∞[.
y = A exp (-20,8 /20)t = A exp(-1,04t) où A est une constante.
2. En déduire la fonction f solution de cette équation différentielle qui vérifie f (0) = 10.
10 = A ; f(t) = 10 e-1,04t.
Partie B :Modèle exponentiel.
On souhaite étudier la croissance de bactéries SA à température
ambiante sur un échantillon de mix (le mix est un mélange contenant en
grande partie du lait permettant la fabrication de glaces à
l’italienne). On suppose que 10 bactéries sont déposées en même temps
sur 1 g de mix. Voici les relevés du nombre de bactéries SA heure par
heure, mesuré à partir du moment où les bactéries sont déposées sur le
mix.
Heure ( ti)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Nombre de bactéries SA ( Ni)
|
10
|
27
|
78
|
232
|
650
|
1800
|
5100
|
14100
|
39000
|
zi
|
2,30
|
3,30
|
4,36
|
5,45
|
6,48
|
7,50
|
8,54
|
9,55
|
10,57
|
1. On effectue un changement de variable de type logarithmique : zi = ln(Ni ).
Compléter le tableau . On arrondira les valeurs au centième.
2. À l’aide de la calculatrice, déterminer une équation de la droite d’ajustement D du nuage de points (ti ; zi ) par la méthode des moindres carrés sous la forme z = at +b. On arrondira les valeurs de a et b au millième.
z=1,037 t +2,301.
3.
En utilisant la question précédente, déterminer une expression de la
fonction N qui modélise le nombre de bactéries SA à l’instant t exprimé
en heures.
N = exp(z) = exp(1,037t +2,301 )= exp(2,301) exp(1,037t = 9,984 exp(1,037t).
Dans la suite, on prendra N(t )= 10e1,04t
pour tout réel t de l’intervalle [0 ; +∞[. On admet que la fonction N
modélise le nombre de bactéries SA relevées sur le mix en fonction du
temps.
4. Une population
donnée de bactéries voit son effectif doubler au bout d’un temps appelé
« temps de génération bactérienne » et noté G. Estimer cette durée G
enminutes.
20 = 10 exp(1,04G) ; ln (2) = 1,04 G ; G = ln(2) / 1,04 heure ou 60 ln(2) / 1,04 minutes ( ~40 min).
5. Calculer la limite de N en +∞.
N tend vers plus l'infini quant le temps devient très grand.
Partie C :Modèle logistique.
Dans cette partie, on étudie et on utilise un deuxième modèle, appelé
modèle logistique et défini par une fonction M, qui, à tout instant t
exprimé en heures, associe le nombre M(t ) de bactéries de SA à
l’instant t donné par :
M(t ) = 13500 / (1350×e−1,04t +1)
1. La dérivée de M est fournie par un logiciel de calcul formel : M′(t )= 13500×1350×1,04×e−1,04t / (1350×e−1,04t +1)2 .
Étudier les variations de la fonction M sur l’intervalle [0 ; +∞[.
Le dénominateur et le numérateur de M' sont positifs.
M(t) est donc strictement croissante sur l’intervalle [0 ; +∞[.
2. a. Déterminer la limite de M en +∞.
Le terme en exponentielle tend vers zéro. M(t) tend vers 13500.
b. L’un des modèles de croissance de bactéries SA (exponentiel ou logistique) est plus vraisemblable. Lequel ?
Le modèle logistique est le plus vraissemblable, le nombre de bactéries cesse de croître quand la nourriture du mix est épuisée.
La courbe représentative de la fonction M est présentée ci-dessous.
3. Déterminer le temps nécessaire pour que le nombre de bactéries SA dépasse 10 000. Arrondir à l’heure.
Pour tout instant t exprimé en heures, le réel M′(t ) est appelé vitesse de prolifération bactérienne.
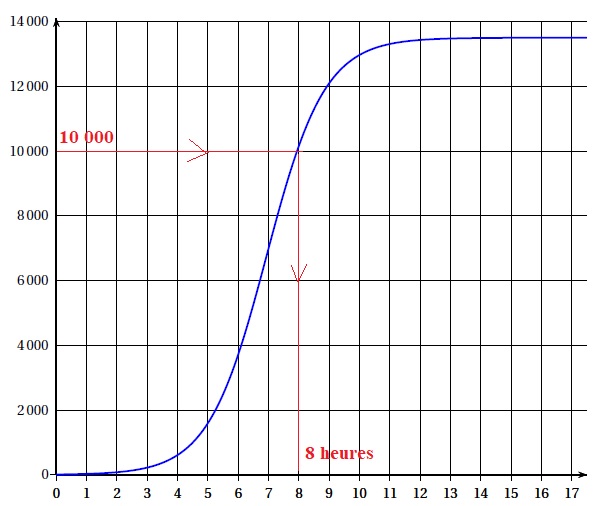
4. Dans cette question, on s’intéresse à l’instant où la vitesse de prolifération bactérienne est
maximale. Parmi les quatre propositions suivantes, une seule d’entre elles correspond à une valeur approchée
de cet instant. Laquelle? Pourquoi ?
a. t = 4 h ; b. t = 7 h ; c. t = 9 h ; d. t = 16 h.
La vitesse correspond à la valeur de la dérivée à la datte t. ( coefficient directeur de la tangente à la courbe )
Le coefficient directeur de la tangente à la courbe est maximal à t = 7 h. ( la tangente est alors la plus inclinée ).
|
...
|
|
Exercice 2. 10 points..
Dans cet exercice, les probabilités seront données en valeurs décimales à 10−4 près.
Les parties A, B et C peuvent se traiter de façon indépendante.
On s’intéresse à la production industrielle de bouteilles d’eau minérale naturelle ou d’eau de source.
On s’intéresse à la qualité de l’eau contenue dans les bouteilles
produites : plusieurs paramètres sont pris en compte, notamment
microbiologiques (présence de bactéries, de coliformes, de germes, . .
. ) et physico-chimiques (présence d’arsenic, de nickel. . . . ).
Partie A : Eau de source et eauminérale naturelle.
En 2017, des analyses identiques ont été menées sur la qualité de l’eau de 126 000 bouteilles produites.
Ainsi 37 000 bouteilles d’eau minérale naturelle et 89 000 bouteilles d’eau de source ont été analysées.
Parmi les analyses portant sur les bouteilles d’eau minérale naturelle,
on constate que 0,12% des analyses révèlent une eau non conforme. Parmi
celles portant sur les bouteilles d’eau de source, on constate que
0,08% des analyses révèlent une eau non conforme.
On choisit le résultat d’une analyse d’une bouteille d’eau au hasard parmi toutes celles qui ont été réalisées.
Dans la suite, on notera les évènements suivants :
M : « L’analyse porte sur une bouteille d’eau minérale naturelle » ;
S : « L’analyse porte sur une bouteille d’eau de source » ;
N : « L’analyse révèle une eau non conforme ».
1. Calculer les probabilités P(M) et P(S).
P(M) =37 / 126 =0,2937 ; P(S) = 89 / 126=0,7063.
Pour les deux questions suivantes, on pourra s’aider d’un arbre pondéré.
2. Calculer la probabilité de choisir une analyse qui révèle une eau non conforme.
3. Calculer la
probabilité qu’une analyse porte sur une bouteille d’eau minérale
naturelle, sachant qu’elle révèle une eau non conforme.
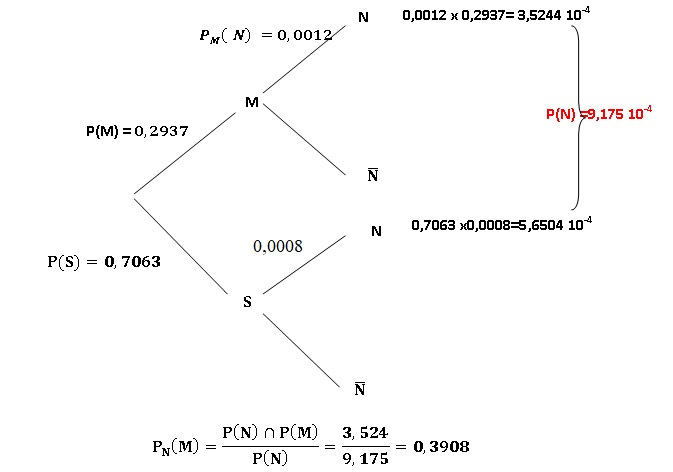
|
....
|
Partie B : Étude du nitrate présent dans l’eau.
Une entreprise produisant des bouteilles d’eau minérale naturelle
affirme que la moyenne du taux de nitrate de sa production est égale à
4,5 mg/L. L’objectif de cette partie est de juger de la véracité de
cette affirmation.
On note μ la moyenne,mesurée en mg/L, du taux de nitrate de la production, et s son écart type.
On réalise 600 prélèvements dans la production. Les résultats sont les suivants :
Taux de nitrate ( mg / L)
|
[4,2 ; 43[
|
[4,3 ; 4,4[
|
[4,4 ; 4,5 [
|
[4,5 ; 4,6 [
|
[4,6 ; 4,7 [
|
[4,7 ; 4,8[
|
Nombre de prélèvements
|
5
|
57
|
181
|
233
|
110
|
14
|
1. En faisant l’hypothèse
que les valeurs observées sont respectivement celles du centre de
chaque classe, déterminer, à l’aide de la calculatrice, la moyenne xmoy et l’écart type s′ de cet échantillon. On donnera les résultats à 10−4 près.
xmoy = 4,5213 ; écart type : s' = 0,09753.
2. Vérifier que s = 0,0976 est un estimateur de l’écart type s.
3. On souhaite réaliser le test bilatéral suivant, au seuil de 5% :
H0 : μ = 4,5 contre H1 : μ diffère de 4,5.
Soit Xmoy
la variable aléatoire qui à tout échantillon de 600 prélèvements
associe la moyenne du taux de nitrate de ces prélèvements. On considère
que Xmoy suit la loi normale d’espérance μ et d’écart type s / 600..
Dans la suite, on remplace s par son estimateur s = 0,0976. Sous l’hypothèse H0, Xmoy suit donc approximativement la loi normale d’espérance 4,5 et d’écart type 0,004.
a. On a présenté les représentations de trois densités de probabilité.
Laquelle est associée à la variable aléatoire Xmoy ? Justifier la réponse.
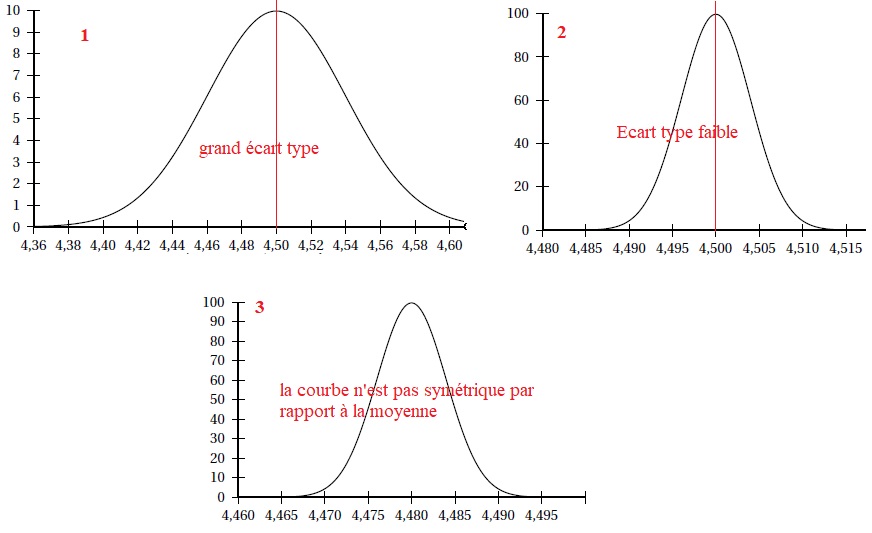
On retient la courbe 2, étroite ( écart type faible) et symétrique par rapport à la moyenne.
b. Donner un nombre réel a à 10−3 près vérifiant : P(4,5−a < Xmoy < 4,5+a) ≈ 0,95.
2 P(Xmoy < 4,5- a )= 1-0,95 = 0,05 ; P(Xmoy < 4,5-a ) = 0,025 ; a = 0,00784.
c. Énoncer la règle de décision de ce test.
Si la moyenne appartient à l'intervalle [4,5 -0,0784 ; 4,5 +0,00784 ) soit [4,492 ; 4,508 ], on retient H0, sinon on retient H1.
d. D’après les résultats obtenus dans l’échantillon donné, peut-on accepter l’hypothèse μ = 4,5 ?
Or xmoy = 4,5213 n'appartient pas à cet intrevalle ; l'hypothèse H1 est retenue.
|
Partie C : Distribution.
L’entreprise
précédente fournit une grande surface en eau minérale. Chaque semaine,
540 bouteilles contenant un litre d’eau minérale sont réceptionnées par
la grande surface.
Une bouteille d’eau minérale d’un litre est de très bonne qualité si elle contient moins de 4,7 mg de nitrate.
On prélève au hasard un lot de 540 bouteilles dans la production, jugée
suffisamment importante pour assimiler ce choix à un tirage avec
remise. On note alors Y la variable aléatoire qui, à chaque lot de 540
bouteilles, associe le nombre de bouteilles de très bonne qualité du
lot.
On admet que Y suit une loi binomiale dont une représentation graphique est fournie ci-dessous :
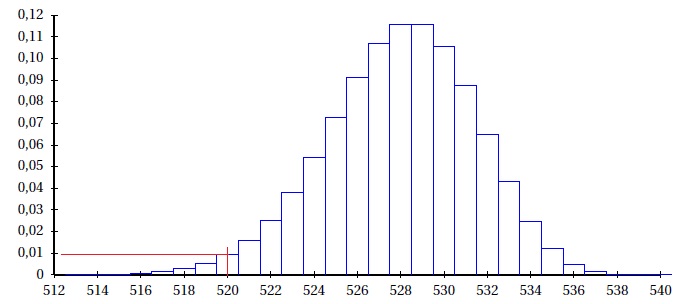
1.
Au vu de ce graphique, un biologiste estime que la probabilité qu’un
lot de 540 bouteilles prélevé au hasard dans la production contienne
moins de 520 bouteilles de très bonne qualité est
environ égal à 0,005. A-t-il raison? Justifier la réponse.
D'après le graphe P(Y < 520 ) est supérieur à 0,01.
2. On admet que le nombre
moyen de bouteilles de très bonne qualité sur l’ensemble des
échantillons de 540 bouteilles est égal à 528.
Donner alors les paramètres n et p de la loi binomiale suivie par la variable aléatoire Y . On arrondira p à 10−3.
n =540 ; p = espérance / n = 528 / 540 = 0,978.
|
|
|